afukuda-06-abstract-clock

/* 
 * Name | Ai Fukuda 
 * Course Section | C 
 * Email | afukuda@andrew.cmu.edu
 * Project | 06
 */ 

function setup() {
    createCanvas(480, 300); 
}

function draw() {
    background(73, 106, 139);
    noStroke();

    // ADDING DESIGN ELEMENTS (FOR AESTHETIC)
    for (y=200; y<300; y+=20) {                // STAR 'TICKS' (BOTTOM LEFT OF CANVAS)
        fill(255, 248, 222);
        for (x=0; x<480; x+=10) {
            if (y%3 == 1) {                       // calling even rows 
                rect(2*x+270, y, 1, 7);
            }
            else {                                // calling odd rows 
                rect(2*x+260, y, 1, 7);  
            }
        } 
    }
    
    push();                                   // SHOOTING STAR LINES 
        stroke(209, 226, 244);
        line(300, 20, 440, 25);
        stroke(206, 236, 236);
        line(300, 30, 440, 45);
        stroke(255, 248, 222);
        line(300, 40, 380, 58);
    pop();

    push();                                  // SHOOTING STAR RECT  
        rectMode(CENTER);
        fill(209, 226, 244);
        rect(455, 26, 5, 5);
        fill(206, 236, 236);
        rect(460, 47, 12, 12);
    pop();

    // ABSTRACT CLOCK ELEMENTS
    var s = second();
    var m = minute();
    var h = hour()%12;     // so hour is given in 12 (not 24)

    // SECOND - 'SHOOTING STAR'
    push();             
        frameRate(40);                                 // defining speed            
        var step = frameCount % 40;
        applyMatrix(1, 0, 0, 1, 40+step, 50+step/3);   // defining slope of 'shooting star' motion 
        fill(255, 248, 222);
        rect(350, 8, 30, 30);
    pop();

    // MINUTE 
    push();
    A = color(255, 250, 195); // light yellow 
    B = color(250, 241, 262); // yellow 
    C = color(254, 232, 147); // yellow yellow orange 
    D = color(255, 228, 183); // yellow orange 
    E = color(253, 205, 167); // orange 
    F = color(253, 210, 194); // orange pink 
    G = color(248, 202, 215); // pink 
    H = color(233, 208, 229); // light pink purple 
    I = color(204, 178, 213); // pink purple 
    J = color(182, 178, 215); // purple 


    interA = lerpColor(A, B, .5);
    interB = lerpColor(B, C, .5);
    interC3 = lerpColor(C, D, .33);
    interC6 = lerpColor(C, D, .66);
    interD3 = lerpColor(D, E, .33);
    interD6 = lerpColor(D, E, .66);
    interE3 = lerpColor(E, F, .33);
    interE6 = lerpColor(E, F, .66);
    interF3 = lerpColor(F, G, .33);
    interF6 = lerpColor(F, G, .66);
    interG = lerpColor(G, H, .5);
    interH3 = lerpColor(H, I, .33);
    interH6 = lerpColor(H, I, .66);
    interI3 = lerpColor(I, J, .33);
    interI6 = lerpColor(I, J, .66);
    // interH = lerpColor(H, I, .5);


        for (z=0; z<m; z++) {         // adding color gradient to minute spectrum                           
            translate(-8, 2.2);
            if (z<2) {              
                fill(A);
            }
            else if (z<4) {
                fill(interA);
            }
            else if (z<6) {
                fill(B);
            }
            else if (z<8) {
                fill(interB);
            }
            else if (z<10) {
                fill(C);
            }
            else if (z<12) {
                fill(interC3);
            }
            else if (z<14) {
                fill(interC6);
            }
            else if (z<16) {
                fill(D);
            }
            else if (z<18) {
                fill(interD3);
            }
            else if (z<20) {
                fill(interD6);
            }
            else if (z<22) {
                fill(E);
            }
            else if (z<24) {
                fill(interE3);
            }
            else if (z<26) {
                fill(interE6);
            }
            else if (z<28) {
                fill(F);
            }
            else if (z<30) {
                fill(interF3);
            }
            else if (z<32) {
                fill(interF6);
            }
            else if (z<34) {
                fill(G);
            }
            else if (z<36) {
                fill(interG);
            }
            else if (z<38) {
                fill(H);
            }
            else if (z<40) {
                fill(interH3);
            }
            else if (z<42) {
                fill(interH6);
            }
            else if (z<44) {
                fill(I);
            }
            else if (z<46) {
                fill(interI3);
            }
            else if (z<48) {
                fill(interI6);
            }
            else {
                fill(J);
            }
            rect(480, 100, z/3, z);
        }
    pop();

    // HOUR 
    push();
    fill(186, 227, 247);
    translate(-92, -92);                                
    arc(100, 100, 300, 300, HALF_PI - radians(7.5*h), HALF_PI);   // shows pie according to hour 
    pop();
} // end of draw function 

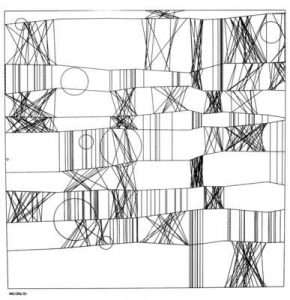
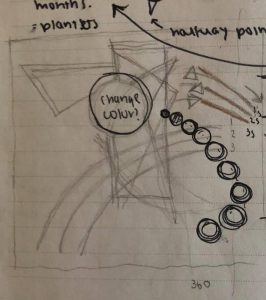
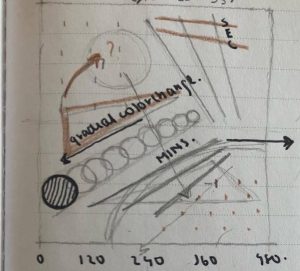
The design of my abstract clock is an abstraction of the solar system; with a shooting star indicating the seconds, the array of planets indicating the minutes and the degree of the sun visible indicating the hour of the current time. Although the different time units are represented distinctively, through the motion/ the flow of its directionality I tried to harmonize them better. One thing I would improve upon is the color gradation seen in the minutes; I feel like there is a much more efficient way to get the same affect.