Project 07: Curves

sketch

/* Samantha Ho
Section E 
sch1@andrew.cmu.edu
Project 07*/

var x;
var y;


function setup() {
	createCanvas(480 , 480);
        frameRate(25);
	}

function draw(){
 background(255, 255, 200);
    
    var nPoints = 20;
    var radius = 250;
    var separation = 125;
    
    // draw the squares in the back
    push();
    translate(2*separation, height / 4);
    for (var i = 0; i < nPoints; i++) {
        var theta = map(i, 0, nPoints, 0, TWO_PI);
        var px = radius * cos(theta);
        var py = radius * sin(theta);
        rect(px - 5, py - 5, 10, 10);
    }
    pop(); 
    
    
    // draw the baseline squiggle 
    strokeWeight(1.5);
    stroke(0,0,255);
    fill(250, 255, 250, 80);
    push();
    translate(2*separation, height /2);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var theta = map(i, 0, nPoints, 0, TWO_PI);
        var px = radius * sin(theta);
        var py = radius * sin(theta);
        vertex(px + random(-5, 10), py + random(-5, 10));
    }
    endShape(CLOSE);
    pop();
    
    //green squiggle
    strokeWeight(1.5);
    stroke(0,190,200);
    fill(0, 195, 220, 80);
    push();
    translate(2*separation, height /2);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var theta = map(i, 0, nPoints, 0, TWO_PI);
        var px = radius * sin(theta);
        var py = radius * sin(theta);
        vertex(px + random(-mouseX/3, 10), py + random(-mouseX/3, 10));
    }
    endShape(CLOSE);
    pop();
    
    //yellow squiggle
    strokeWeight(1.5);
    stroke(0,190,200);
    fill(255, 255, 0, 80);
    push();
    translate(2*separation, height /2);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var theta = map(i, 0, nPoints, 0, TWO_PI);
        var px = radius * sin(theta);
        var py = radius * sin(theta);
        vertex(px + random(-mouseX/3, 10), py + random(-mouseX/3, 10));
    }
    endShape(CLOSE);
    pop();
  
}

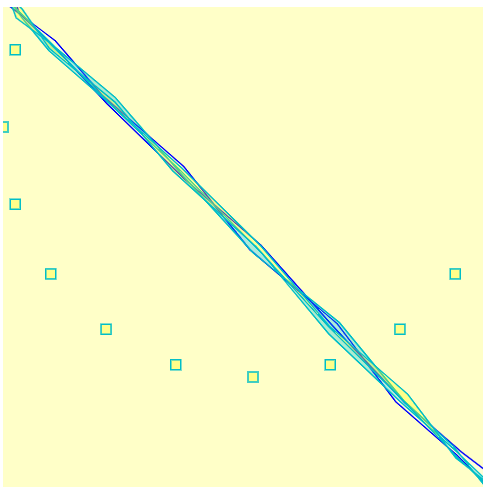
After playing around with the circles and the graphs, I liked the animated rendering effect so I continued to play around. I created this layered squiggle and baseline whose form is contingent on the cursor’s X-position.