Sharpening your Skillz.
Below are 20 brief exercises. Execute as many as you can before class on Wednesday, 9/23. Find a balance between banging this work out, and making your sketches look reasonably nice.
In a blog post:
- Provide links to the 20 sketches at the online p5.js web editor.
- Provide a screenshot of each program, or an animated GIF if you prefer.
- Unless you have other goals, make all of your sketches 600×600.
- Categorize your blog post, 04-Exercises
- Title your blog post, nickname-Exercises
Exercises
01. One with Everything
Seriously take 5 minutes to browse the p5.js Reference. Explore your graphics toolset by drawing one of each type of primitive it provides. For example: draw a rectangle, rounded-rectangle, ellipse, arc, line segment, Bézier curve, polyline, and multi-sided polygon. Experiment with their rendering options and parameters, such as fill color, stroke weight, closed or open, etc. Using push(), rotate(), translate(), and pop(), draw one shape rotated by 30°.
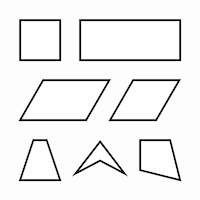
02. Quadrilateral Zoo
Write commands to plot the vertices of a family of quadrilaterals: square, rectangle, parallelogram, rhombus, trapezoid, dart, and kite. You’re not permitted to use the rect() command. (Can you add a control parameter to them, that links their form to the position of the cursor?)
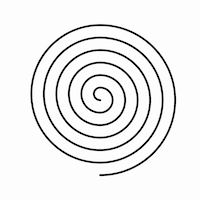
03. Spiral
Write a program that draws a spiral. Before you begin, check into different types of spirals, such as Archimedes’s spiral (the radius of which grows arithmetically) and the logarithmic or equiangular spiral (whose radius grows geometrically). Consider different implementations, such as explicitly plotting your spiral using polar equations, implicitly rendering it by summing small differences (e.g. go forward, turn slightly, repeat), or approximating it piecewise with circular arcs.
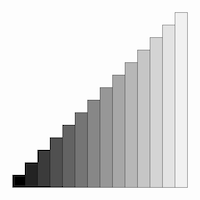
04. Transitioning Rectangles
Recall that any visual property can be linked to a loop variable, not just position. Use iteration to generate a series of rectangles. Your code should simultaneously control several of the rectangles’ visual properties, including their position, height, and fill color. (Are you able to use a shaping function to make the transition non-linear?) Consider using the map(), lerp(), and lerpColor() commands.
05. Iteration with Functions
Write a function that encapsulates the code to render a simple visual element (a leaf, face, etc.). Give your function arguments that determine where the element will be positioned. Using iteration, call your function to display a grid of these elements.
06. Random Splat
Plot the vertices of a many-sided polygon, using the functions sin() and cos() in the same way that you might generate a circle, but compute the position of each point with a radius that is slightly randomized. How closely can you make the result resemble a drop of ink? Consider using the beginShape(), vertex(), and endShape() commands.
07. Stochastic Elements
Create an evocative composition in which an iterative loop deposits small elements in random locations around the canvas. These elements might look like craters, potholes, pimples, ants, chocolate chips, holes in Swiss cheese…
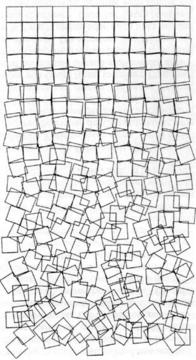
08. Recoding Schotter
Schotter by Georg Nees (1968) is a classic algorithmic computer artwork, now more than 50 years old, that depicts a gradient from order to chaos across a 12×22 grid of squares. In it, the squares’ orientations become increasingly randomized towards the bottom of the page. Re-code this work, paying attention to detail.
09. Billiard Ball
Create a sketch with a moving ball that bounces off the edges of the canvas. Take care that the ball never appears to overlap the edge of the canvas. Suggestion: give the ball position and velocity variables; flip the sign of the velocity variables when the ball encounters the edge of the canvas.
10. One-Person Pong
Create a sketch that recreates the game of Pong for a single user. Can you add a scoring system?
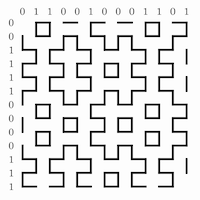
11. Hitomezashi Sashiko Stitching
Randomly label the columns and rows of a grid with 0s and 1s. For each column, draw a vertical sequence of alternating dashes and gaps, beginning with a dash (for columns labeled 1) or a gap (for columns labeled 0). Similarly, draw horizontal sequences of dashes and gaps for the rows. Observe the resulting patterns.
As promised, here is @maths_kath’s #mathartchallenge!
Based on traditional Japanese stitching, this is a riff on hitomezashi patterns. Using grid paper, give each line (vertical & horizontal) a 0 or 1. (See pictures below, too,) “Stitch” each line accordingly. #mtbos #mathart pic.twitter.com/6i0zYx2rI4
— Annie Perkins (@anniek_p) March 29, 2020
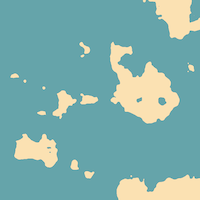
12. Imaginary Islands
Use a two-dimensional Perlin noise function to generate a map of imaginary islands. For every pixel: if the value of the noise function is below some threshold value, color the pixel blue (for water); if it is higher than the threshold, color it brown (for land). You will want to use the noise() (with two arguments), noiseDetail(), set(), and updatePixels() functions in p5.js.
13. Drawn Line, Three Ways
Create an interaction that stores the past 100 mouse positions, and displays them as a polyline. Store the mouse data in three different ways: in two 1D arrays (one for X, one for Y); in one 2D array; and in an array of Point2D objects.
14. Calligraphic Polyline
Create a sketch that stores the past 100 mouse positions. Draw a line between each point and the one previous to it. Make the thickness of this line (e.g. strokeWeight(), or some other visual technique) inversely proportional to the distance between each pair of points, so that faster marks make thinner lines.
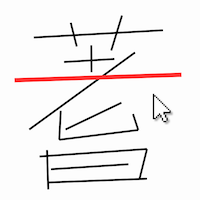
15. Longest Line Search
Write a program that accumulates an array of straight line segments when the user clicks and drags. Color the longest line red.
16. Eyes Following Cursor
Draw one or more eyes with pupils that follow the cursor. If you can, constrain each pupil to stay within its eyeball.
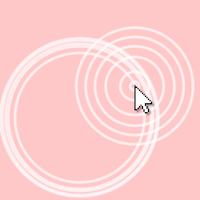
17. Ripples in a Pond
Create a program in which animated circular “ripples” emanate outward from the cursor each time the mouse button is clicked. Consider the speed at which your ripples expand. Implement your ripples in an object-oriented coding style. See this p5.js example for an array of objects in p5.js.
18. Butt Generator
Write a program that uses arcs or Bézier curves to generate one or more butts.
19. Angle between Three Points
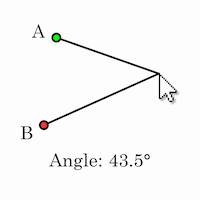
Write a program that computes the interior angle between three points: two randomly placed points, A and B, and the mouse cursor, C. Hint: Use the dot product to compute the angles, and use the cross product to distinguish positive from negative curvature. The atan2() function could also be helpful.
20. Circle from Three Points (Circumcenter)
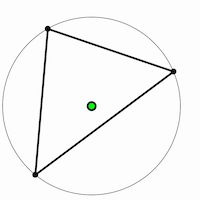
Construct a random triangle whenever a button is pressed. Generate a circle that passes precisely through all three of its vertices. The center of this circle is called the circumcenter of the triangle. Place a dot there. Note: the circumcenter is not always inside the triangle. See this page for help with the math.