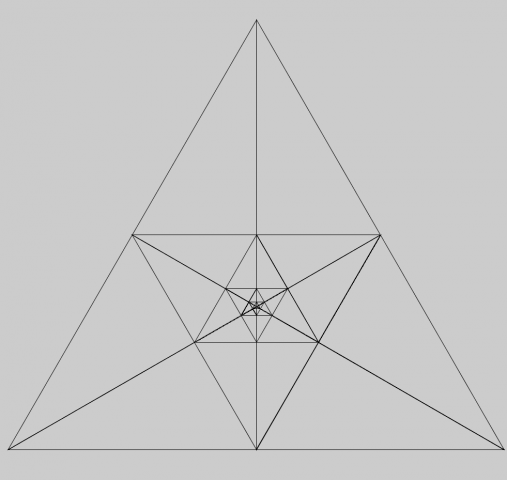
I wanted to do a modified version of an Sierpinski diagram. It was pretty fun to mess around with beginShape(), endShape(), and for loops. I wanted to make it more complex, but I got sleepy from the trig.
I can change the depth and size of the diagram at will, which is nice.
Code is below the read more.
import processing.svg.*;
float ax, ay, bx, by, cx, cy;
void setup(){
size(1000, 1000);
surface.setLocation(50,50);
noFill();
noLoop();
beginRecord(SVG, "output.svg");
}
void draw(){
beginShape();
for(int i = 0; i < 7; i++){
nestedTri(width/2, height/2+100, pow(2,i)*15,60*i);
//nestedTri(width/2, height/2+100, pow(2,i)*100,60*i);
}
vertex(width/2,height/2+100);
endShape();
endRecord();
}
void nestedTri(float x, float y, float size, int angle){
//x,y is midpoint location
//size is side length
//want to start at side, end at 1st hit vertex after drawing others
float apo = ((size/2)*sqrt(3))/3;
float x_, y_,a;
a = radians(angle);
//begin shape/end shape cannot contain rotate,
//so i must do all of the rotations by hand
x_ = x + (0*cos(a) - (apo)*sin(a));
y_ = y + (0*sin(a) + (apo)*cos(a));
vertex(x_,y_);
x_ = x + ((size/2)*cos(a) - (apo)*sin(a));
y_ = y + ((size/2)*sin(a) + (apo)*cos(a));
ax = x_;
ay = y_;
vertex(ax,ay);
vertex(x,y);
vertex(ax,ay);
x_ = x + (0*cos(a) - (-2*apo)*sin(a));
y_ = y + (0*sin(a) + (-2*apo)*cos(a));
bx = x_;
by = y_;
vertex(bx,by);
vertex(x,y);
vertex(bx,by);
x_ = x+ ((-size/2)*cos(a) - (apo)*sin(a));
y_ = y+ ((-size/2)*sin(a) + (apo)*cos(a));
cx = x_;
cy = y_;
vertex(cx,cy);
vertex(x,y);
vertex(cx,cy);
vertex(ax,ay);
}