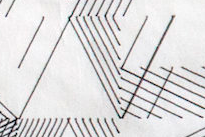
I dunno if I’m crazy, but I think the p5 svg thing breaks the pop() function, so I learned how to invert my goddang transformations.
let dosvg = true;
const edgeRoom = 30;
const Wm = 12;
const Hm = 12;
const Lm = 40;
const Sw = dosvg ? 0.8 : 0.015;
function diags(d) {
push();
let dangus = randomHalf();
for (let i = -d + 1; i < d; i++) {
let x0 = constrain(map(i, 0, d, 0, 1), 0, 1);
let x1 = constrain(map(i, 0, d, 1, 2), 0, 1);
let y0 = constrain(map(i, -d, 0, 1, 0), 0, 1);
let y1 = constrain(map(i, 0, d, 1, 0), 0, 1);
if (isNaN(x0) || isNaN(x1) || isNaN(y0) || isNaN(y1)) console.log('dingus');
strokeWeight(Sw);
line(x0,y0,x1,y1);
}
unRandomHalf(dangus);
pop();
}
function halfdiags(d) {
push();
let dangus = randomHalf();
for (let i = 0; i < d; i++) {
let x0 = constrain(map(i, 0, d, 0, 1), 0, 1);
let x1 = constrain(map(i, 0, d, 1, 2), 0, 1);
let y0 = constrain(map(i, -d, 0, 1, 0), 0, 1);
let y1 = constrain(map(i, 0, d, 1, 0), 0, 1);
if (isNaN(x0) || isNaN(x1) || isNaN(y0) || isNaN(y1)) console.log('dingus');
strokeWeight(Sw);
line(x0,y0,x1,y1);
}
unRandomHalf(dangus);
pop();
}
function tri(d) {
push();
let dangus = randomHalf();
for (let i = 0; i < d; i++) {
let x0 = constrain(map(i, 0, d, 0, 1), 0, 1);
let x1 = constrain(map(i, 0, d, 0.5, 1), 0, 1);
let y0 = 0; //constrain(map(i, -d, 0, 1, 0), 0, 1);
let y1 = constrain(map(i, 0, d, 1, 0), 0, 1);
if (isNaN(x0) || isNaN(x1) || isNaN(y0) || isNaN(y1)) console.log('dingus');
strokeWeight(Sw);
line(x0,y0,x1,y1);
}
unRandomHalf(dangus);
pop();
}
function f0() {
diags(2);
}
function f1() {
diags(5);
}
function f2() {
diags(7);
}
function f3() {
diags(11);
}
function f4() {
halfdiags(2);
}
function f5() {
halfdiags(5);
}
function f6() {
halfdiags(7);
}
function f7() {
halfdiags(11);
}
function f8() {
halfdiags(1);
}
function f9() {
tri(5);
}
function f10() {
tri(7);
}
function f11() {
diags(4);
}
function f12() {
halfdiags(4);
}
function para(d) {
push();
let dangus = randomQuarter();
for (let i = 1; i < d; i++) {
let x0 = map(i, 0, d, 0, 1);
let x1 = 1;
let y0 = 0;
let y1 = map(i, 0, d, 0, 1);
if (isNaN(x0) || isNaN(x1) || isNaN(y0) || isNaN(y1)) console.log('dingus');
strokeWeight(Sw);
line(x0,y0,x1,y1);
}
unRandomQuarter(dangus);
pop();
}
function f13() {
para(3);
}
function f14() {
para(5);
}
let sectionFunctions = [f0, f1, f1, f2, f2, f3, f4, f5, f5, f6, f6, f7, f8, f0, f1, f1, f2, f2, f3, f4, f5, f5, f6, f6, f7, f8, f9, f10, f11, f12, f0, f1, f1, f2, f2, f3, f4, f5, f5, f6, f6, f7, f8, f0, f1, f1, f2, f2, f3, f4, f5, f5, f6, f6, f7, f8, f9, f10, f11, f12, f13, f14];
function setup() {
if (dosvg) createCanvas(2*edgeRoom + Wm*Lm, 2*edgeRoom + Hm*Lm, SVG);
else createCanvas(2*edgeRoom + Wm*Lm, 2*edgeRoom + Hm*Lm);
noLoop();
}
function draw() {
drawVera();
/*push();
translate(10,100);
scale(0.99,0.5);
line(0,0,width,height);
pop();*/
}
function drawVera() {
//let bg = 240;
//background(bg);
clear();
stroke(0);
//strokeWeight(0.015);
strokeWeight(Sw);
noFill();
for (let i = 0; i < Hm; i++) {
for (let j = 0; j < Wm; j++) {
/*line(edgeRoom + j*Lm, edgeRoom + i*Lm,
edgeRoom + j*Lm + Lm*0.6, edgeRoom + i*Lm + Lm*0.8);*/
push();
translate(edgeRoom + j*Lm, edgeRoom + i*Lm);
scale(Lm);
//line(0,0,0.8,0.8);
drawSection();
scale(1/Lm);
translate(-edgeRoom - j*Lm, -edgeRoom - i*Lm);
pop();
}
}
//fill(bg);
//noStroke();
//rect(0,0,edgeRoom,height);
//rect(width - edgeRoom,0,edgeRoom,height);
}
function keyPressed() {
saveSVG("vera.svg");
}
function drawSection() {
//line(0, 0, 0.8, 0.8);
let r = Math.random();
let numSections = r < 0.02 ? 0 : r < 0.1 ? 1 : r < 0.8 ? 2 : 3;
for (let s = 0; s < numSections; s++) {
let i = Math.floor(Math.random() * sectionFunctions.length);
let f = sectionFunctions[i];
f();
}
}
function randomHalf() {
let vertical = Math.random() < 0.5 ? 1 : 0;
let horizontal = 1 - vertical;
let offset = Math.random() < 0.5 ? 1 : 0;
let fh = Math.random() < 0.5; //flip horizontal
let fv = Math.random() < 0.5; //flip vertical
scale(1 - 0.5*vertical, 1 - 0.5*horizontal);
translate(vertical * offset, horizontal * offset);
if (fh) {
scale(-1, 1);
translate(-1, 0);
}
if (fv) {
scale(1, -1);
translate(0, -1);
}
return {vertical, horizontal, offset, fh, fv};
}
function unRandomHalf(dangus) {
let {vertical, horizontal, offset, fh, fv} = dangus;
if (fv) {
translate(0, 1);
scale(1, -1);
}
if (fh) {
translate(1, 0);
scale(-1, 1);
}
translate(-vertical * offset, -horizontal * offset);
scale(1 / (1 - 0.5*vertical), 1 / (1 - 0.5*horizontal));
}
function randomQuarter() {
let x = Math.random() < 0.5 ? 1 : 0;
let y = Math.random() < 0.5 ? 1 : 0;
let f1 = Math.random() < 0.5;
let f2 = Math.random() < 0.5;
scale(0.5,0.5);
translate(x, y);
if (f1) {
scale(-1, 1);
translate(-1, 0);
}
if (f2) {
scale(1, -1);
translate(0, -1);
}
return {x, y, f1, f2};
}
function unRandomQuarter(z) {
let {x, y, f1, f2} = z;
if (f2) {
translate(0, 1);
scale(1, -1);
}
if (f1) {
translate(1, 0);
scale(-1, 1);
}
translate(-x, -y);
scale(2,2);
}

 ^^ pixel image (from before I messed up the code) ^^
^^ pixel image (from before I messed up the code) ^^
 ^^ I also experimented with color ^^
^^ I also experimented with color ^^