Team Members: Alia Friedman, Ariel Uy, Hiroshi Wu, Jessica Xiao, Joshua Cheng
Our show features a visual presentation of five mathematical sequences: Perfect Squares, Pi, Fibonacci Sequence, Prime Numbers, and the Pythagorean Theorem. While mathematical sequences are inherently numerical, the visualization of these sequences and their proofs can be quite beautiful. Therefore, we not only present the sequences themselves, but also an explanation of the mathematical concepts behind each sequence. Mathematics is very important to computer science, engineering, and many other fields, and we think that CMU students would appreciate this display. We hope that our display will bridge both the artistic and technical communities at CMU.
Part1: Perfect Squares
The first part of the show exhibited the number-line format of perfect squares, where we count towards each square. However, the beauty of perfect squares reveals itself when all the numbers are shown on a square and the perfect squares form a diagonal. We emphasize this beauty by eventually showcasing how the numbers gradually build from the side and middle and expand outwards at every step.

Part2: Fibonacci Sequence
The second part of the show illustrates the Fibonacci sequence along the span of the bridge, with each number in the sequence being represented by the spacing between the distinct orange panels. The orange panels light up gradually from left to right, representing the concept of growth associated with the Fibonacci sequence.
The Fibonacci sequence can be found in many real-world applications such as art and nature. Therefore, we sought to represent these concepts through the background colors, using a Python script to automatically generate the background colors from images of art and nature. This result in an interesting blend of colors that complemented the distinct orange panels.

Part3: Pythagorean Theorem
First discovered in ancient Greece, the Pythagorean Theorem can be used to find the hypotenuse of a right triangle using the two other sides.
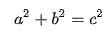
In this section of the show, the number of light panels represented a and b. The numbers were then squared and the panels corresponding to those numbers were illuminated. The numbers were then amount added together and their colors were also blended in order to arrive at C^2. The number’s square root was then taken and the corresponding amount of panels were illuminated. In the picture above we can see nine panels being added to 16 panels, in order to arrive at 25 representing a side C of five.

Part4: Prime Numbers
Prime numbers are the building blocks of the integers, and they are an important part of many areas of mathematics and computer science. In this section of the show, the prime numbers are visualized using the Sieve of Eratosthenes, which is a simple method to derive the primes. The bridge itself is a number line from Gates to Purnell. First, all multiples of 2 are colored purple, then all multiples of 3 are colored blue, and so on, leaving only the prime numbers in bright white. The visualization brings a pattern and a motivation to the prime numbers.

Part5: Pi
Pi is integral to our world; wherever a circle exists, pi exists. I tried to show how pi integrates in a few scenarios, such as unravelling a circle, and in sine wave oscillations. These are both represented as moving lights on the bridge. Pi is also an interesting transcendental number in that no patterns have been found in the decimal representation, so it’s a good source of randomness, which I exhibited as colorings of the bridge. Overall I hoped to show both the structural and chaotic aspect of Pi and how that integrates in the world, and the hidden beauty in both structure and chaos.

Video:
https://drive.google.com/file/d/1iA6cFHkD32PKogVPYSOVy0geqVCtS_RS/view?usp=sharing