Goal
Our goal was to create the movement of a front kick that a human could produce. We started off getting a double pendulum in a Python Template to replicate the general motion of the dynamic movement.
Outcomes
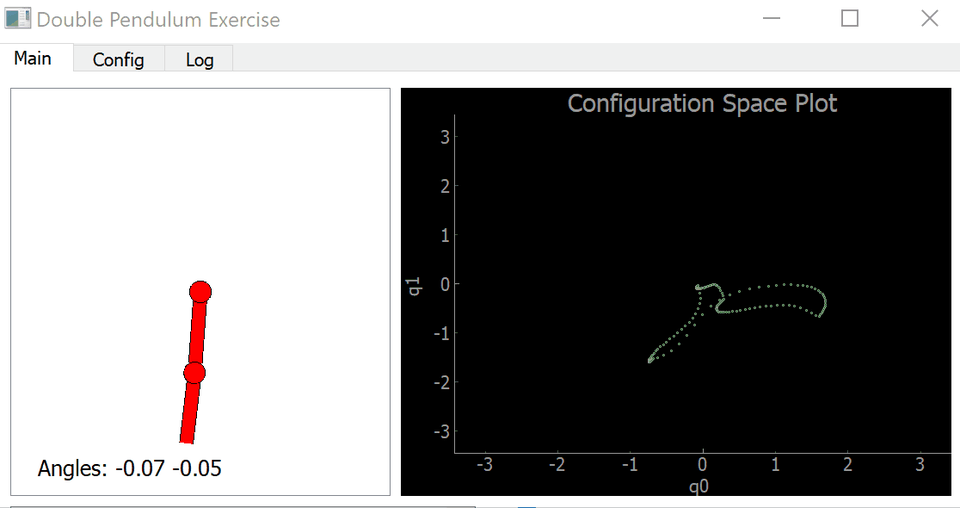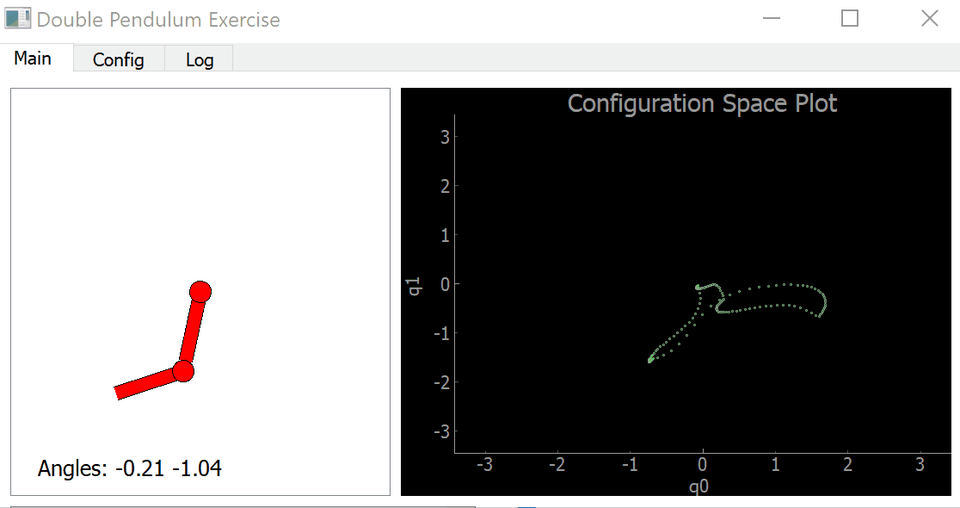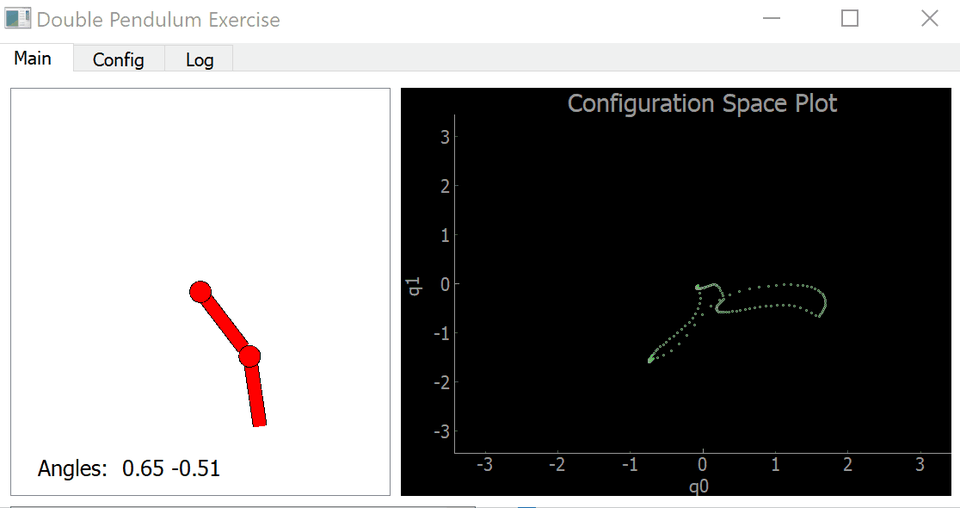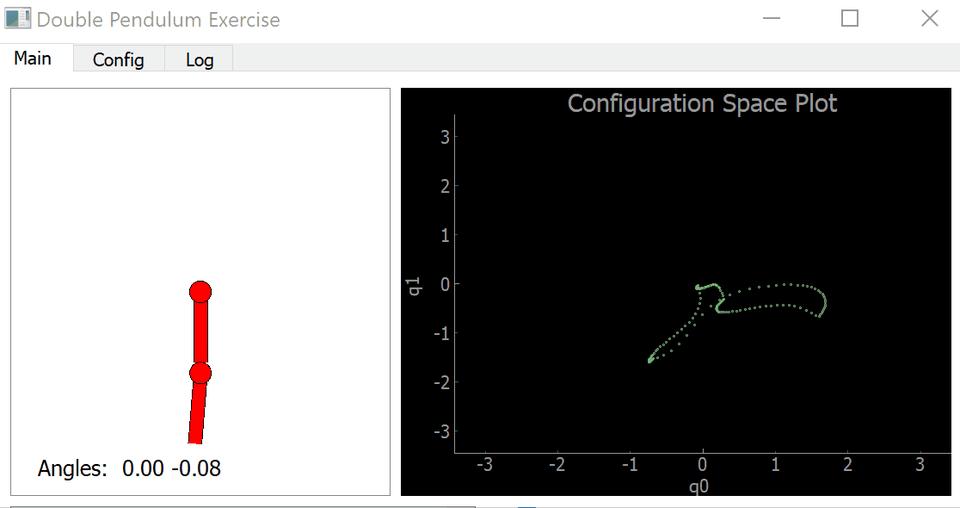
If we could have done it better another time, we would have made the motion more realistic/natural. We attempted to do that with minimal PID Control by adjusting the double pendulum .py file where we adjusted the Dampening . We added keyframes that are specific to our motion but we did not figure out a way to increase the number of keyframes in the loop.
Code
dblpend_keyframes.py
#!/usr/bin/env python3
"""Prototype Python 3 script for the 16-375 double-pendulum control exercise."""
################################################################
# Written in 2018-2019 by Garth Zeglin <garthz@cmu.edu>
# To the extent possible under law, the author has dedicated all copyright
# and related and neighboring rights to this software to the public domain
# worldwide. This software is distributed without any warranty.
# You should have received a copy of the CC0 Public Domain Dedication along with this software.
# If not, see <http://creativecommons.org/publicdomain/zero/1.0/>.
################################################################
import math
import numpy as np
import rcp.doublependulum
from rcp.ex.dblpend import main
################################################################
class PendulumController(rcp.doublependulum.DoublePendulumController):
def __init__(self):
super().__init__()
# for this example, there are four fixed poses commanded a fixed intervals, expressed as a set of (q0, q1) pairs
self.keyframes = np.zeros((4,2))
self.last_frame = None
return
#================================================================
def setup(self):
self.write("""Keyframed position control demonstration.
Applies a sequence of joint targets to a position controller at fixed intervals.
The parameter sliders 0 and 1 control the 'shoulder' and 'elbow' angles for the first keyframe, 2 and 3 are the second keyframe, etc.
""")
return
#================================================================
def user_parameter_change(self, parameter, value):
pose = parameter // 2
joint = parameter % 2
if pose < len(self.keyframes):
self.keyframes[pose][joint] = 2 * math.pi * (value - 0.5)
self.write("Set pose %d joint %d to angle %f" % (pose, joint, self.keyframes[pose][joint]))
def apply_configuration(self, config):
self.keyframes[0,:] = [-1.42,-1.95]
self.keyframes[1,:] = [2.5,-0.3]
self.keyframes[2,:] = [0.625,-0.36]
self.keyframes[3,:] = [-0.1,-0.07]
return
# if 'keyframes' in config:
# for i in range(len(self.keyframes)):
# q0 = config['keyframes'].getfloat('keyframe-%d-q0' % i, fallback = 0.0)
# q1 = config['keyframes'].getfloat('keyframe-%d-q1' % i, fallback = 0.0)
# self.keyframes[i,:] = [q0, q1]
# return
def gather_configuration(self, config):
if 'keyframes' not in config:
config['keyframes'] = {}
for i in range(len(self.keyframes)):
config['keyframes']['keyframe-%d-q0' % i] = str(self.keyframes[i, 0])
config['keyframes']['keyframe-%d-q1' % i] = str(self.keyframes[i, 1])
return
#================================================================
def compute_control(self, t, dt, state, tau):
"""Method called from simulator to calculate the next step of applied torques.
:param t: time in seconds since simulation began
:param state: four element numpy array with joint positions ``q`` and joint velocities ``qd`` as ``[q0, q1, qd0, qd1]``, expressed in radians and radians/sec
:param tau: two element numpy array to fill in with the joint torques to apply ``[tau0, tau1]``
"""
# select the current keyframe based on the time
frame = int(t // 1.5)
if frame != self.last_frame:
self.write("Starting frame %d" % frame)
self.last_frame = frame
# select the pose for the current keyframe, looping over the available poses
pose = self.keyframes[frame % len(self.keyframes)]
# create a target state by extending the pose to include velocity
target = np.concatenate((pose, np.zeros(2)))
# calculate position and velocity error as difference from reference state
qerr = target - state
# apply PD control to reach the pose (no integral term)
tau[0] = (self.kp[0] * qerr[0]) + (self.kd[0] * qerr[2])
tau[1] = (self.kp[1] * qerr[1]) + (self.kd[1] * qerr[3])
return
################################################################$
if _name_ == "_main_":
main(PendulumController)
doublependulum.py
# Standard library modules.
import math, time, threading, queue, logging
# Third-party library modules.
import numpy as np
# set up logger for module
log = logging.getLogger(_file_)
################################################################
class DoublePendulumController(object):
"""Prototype for a double-pendulum controller. This class is typically subclassed to customize the control strategy and the subclass passed into the common application framework.
:ivar initial_state: four-element numpy array used to initialize the simulator state: [q1, q2, qd1, qd2]
:ivar kp: two-element numpy array with default proportional position gains
:ivar ki: two-element numpy array with default integral gains
:ivar kd: two-element numpy array with default velocity damping gain
"""
def __init__(self):
# delegate object to which debugging and status messages can be printed; it must implement write()
self.console = None
# fixed controller parameters
self.initial_state = np.array([0.0, 0.0, 0.0, 0.0])
self.d_state = np.array((1.0, 0.5*math.pi, 0.0, 0.0))
self.kp = np.array((16.0, 8.0))
self.ki = np.array((4.0, 2.0))
self.kd = np.array((10.0, 2.0))
return
#================================================================
def connect_console(self, console):
"""Attach a console object to be used for debugging output. The object needs to implement write()."""
self.console = console
return
def write(self, string):
"""Write a message to the debugging console. If console is not available, writes to the log as an info message."""
if self.console is not None:
self.console.write(string)
else:
log.info(string)
return
def setup(self):
"""Hook for final one-time object configuration. This is called once prior to the start of the simulation. The default implementation does nothing."""
pass
def user_parameter_change(self, parameter, value):
"""Hook for interactive parameter changes (e.g. GUI sliders). The default implementation does nothing.
:param parameter: integer index of parameter, starting with zero
:param value: dimensionless parameter value, ranges from zero to one inclusive.
"""
pass
#================================================================
def apply_configuration(self, config):
"""Hook for applying parameters saved in a configuration file. The default implementation does nothing.
:param config: configparser object (which implements the mapping protocol)
"""
pass
def gather_configuration(self, config):
"""Hook for saving parameters in a configuration file. The default implementation does nothing.
:param config: configparser object (which implements the mapping protocol)
"""
pass
#================================================================
def compute_control(self, t, dt, state, tau):
"""Method called from numerical pendulum simulation to calculate the next step of applied torques. This is usually overridden in a subclass, but the default implementation applies a fixed-target PD position control.
:param t: time in seconds since simulation began
:param state: four element ndarray of joint positions q and joint velocities qd as [q1, q2, qd1, qd2], expressed in radians and radians/sec
:param tau: two element ndarray to fill in with joint torques to apply
"""
# convenience variables to notate the state variables
q1 = state[0] # 'shoulder' angle in radians
q2 = state[1] # 'elbow' angle in radians
qd1 = state[2] # 'shoulder' velocity in radians/second
qd2 = state[3] # 'elbow' velocity in radians/second
# calculate position and velocity error as difference from reference state
qerr = self.d_state - state
# apply PD control to reach the pose (no integral term)
tau[0] = (self.kp[0] * qerr[0]) + (self.kd[0] * qerr[2])
tau[1] = (self.kp[1] * qerr[1]) + (self.kd[1] * qerr[3])
return
################################################################
class DoublePendulumSimulator(object):
"""Numerical dynamic simulation of a frictionless double pendulum. It
communicates with a user-supplied control object to compute applied joint
torques.
"""
def __init__(self):
# the object used to calculate joint torques
self.control = None
# set default dynamics
self.set_default_dynamic_parameters()
# configure transient state
self.reset()
return
def connect_controller(self, controller):
"""Attach a controller object used to compute joint torques and set the initial state."""
self.control = controller
self.reset()
return
def reset(self):
"""Reset or initialize all simulator state variables."""
self.t = 0.0
self.dt = 0.001
if self.control is not None:
self.state = self.control.initial_state.copy()
else:
self.state = np.array([0.0, 0.0, 0.0, 0.0])
self.tau = np.array([0.0, 0.0])
self.dydt = np.ndarray((4,))
return
def set_default_dynamic_parameters(self):
"""Set the default dynamics coefficients defining the rigid-body model physics."""
self.l1 = 1.0 # proximal link length, link1
self.l2 = 1.0 # distal link length, link2
self.lc1 = 0.5 # distance from proximal joint to link1 COM
self.lc2 = 0.5 # distance from distal joint to link2 COM
self.m1 = 1.0 # link1 mass
self.m2 = 1.0 # link2 mass
self.I1 = (self.m1 * self.l1**2) / 12 # link1 moment of inertia
self.I2 = (self.m2 * self.l2**2) / 12 # link2 moment of inertia
self.gravity = -9.81
return
#================================================================
def deriv(self):
"""Calculate the accelerations for a rigid body double-pendulum dynamics model.
:returns: system derivative vector as a numpy ndarray
"""
q1 = self.state[0]
q2 = self.state[1]
qd1 = self.state[2]
qd2 = self.state[3]
LC1 = self.lc1
LC2 = self.lc2
L1 = self.l1
M1 = self.m1
M2 = self.m2
d11 = M1*LC1*LC1 + M2*(L1*L1 + LC2*LC2 + 2*L1*LC2*math.cos(q2)) + self.I1 + self.I2
d12 = M2*(LC2*LC2 + L1*LC2*math.cos(q2)) + self.I2
d21 = d12
d22 = M2*LC2*LC2 + self.I2
h1 = -M2*L1*LC2*math.sin(q2)*qd2*qd2 - 2*M2*L1*LC2*math.sin(q2)*qd2*qd1
h2 = M2*L1*LC2*math.sin(q2)*qd1*qd1
phi1 = -M2*LC2*self.gravity*math.sin(q1+q2) - (M1*LC1 + M2*L1) * self.gravity * math.sin(q1)
phi2 = -M2*LC2*self.gravity*math.sin(q1+q2)
# now solve the equations for qdd:
# d11 qdd1 + d12 qdd2 + h1 + phi1 = tau1
# d21 qdd1 + d22 qdd2 + h2 + phi2 = tau2
rhs1 = self.tau[0] - h1 - phi1
rhs2 = self.tau[1] - h2 - phi2
# Apply Cramer's Rule to compute the accelerations using
# determinants by solving D qdd = rhs. First compute the
# denominator as the determinant of D:
denom = (d11 * d22) - (d21 * d12)
# the derivative of the position is trivially the current velocity
self.dydt[0] = qd1
self.dydt[1] = qd2
# the derivative of the velocity is the acceleration.
# the numerator of qdd[n] is the determinant of the matrix in
# which the nth column of D is replaced by RHS
self.dydt[2] = ((rhs1 * d22 ) - (rhs2 * d12)) / denom
self.dydt[3] = (( d11 * rhs2) - (d21 * rhs1)) / denom
return self.dydt
#================================================================
def timer_tick(self, delta_t):
"""Run the simulation for an interval.
:param delta_t: length of interval in simulated time seconds
"""
while delta_t > 0:
# calculate next control outputs
self.control.compute_control(self.t, self.dt, self.state, self.tau)
# calculate dynamics model
qd = self.deriv()
# Euler integration
self.state = self.state + self.dt * qd
delta_t -= self.dt
self.t += self.dt
################################################################
Comments are closed.