Assignment 14 – Elise and Kanvi

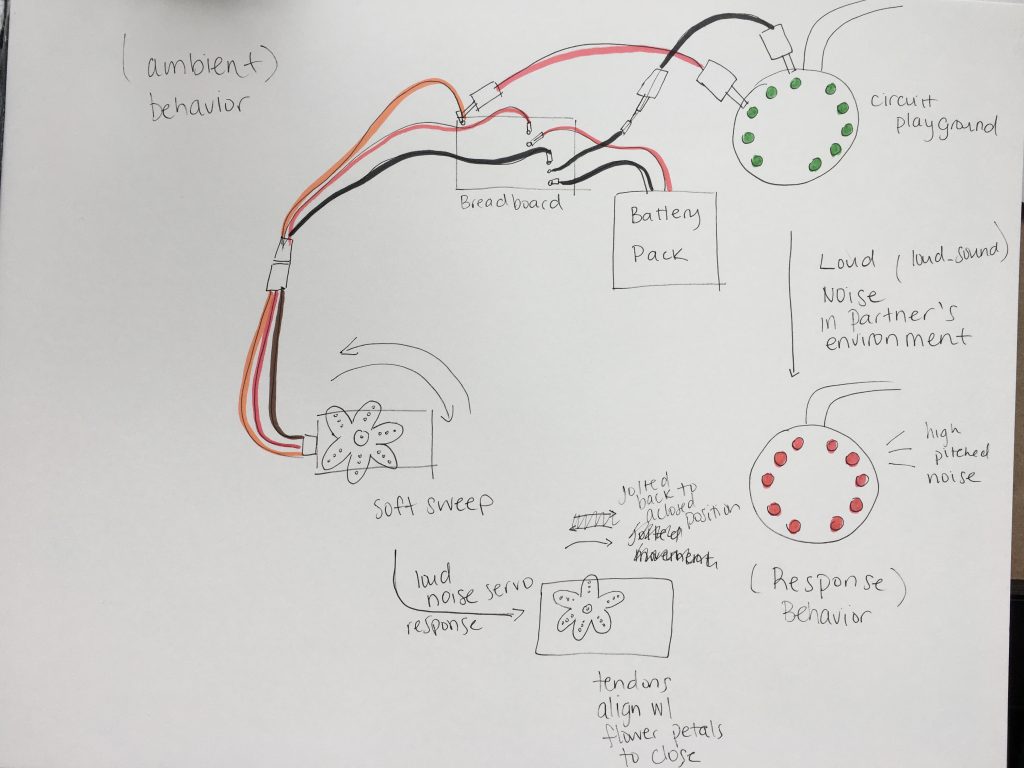
The mechanism for our flower involves a sine servo motion with green lights when at rest. The servo then reacts to a loud noise such as a snap if our test video as well as with a jolt in motion to close the flower. The Red LED lights turn on, and a high-pitched tone pursues for a second or two. After about 10 seconds, the servo returns back to its peaceful state.

Our sketch describes the minimal mechanics and intended response outcomes. With a loud noise on Kanvi’s side, the motion of Elise’s motor would jolt towards a stop to close the petals or vice versa. The jolt with be the servo going back to starting position such that the tendons attached will overlap with the petals.

Changes to be made in the future

Right now, our code uses the “loud_noise” function provided in the cp library but this isn’t sensitive enough for our purpose. We will be working on finding the perfect sound level to make the reaction of the flower more meaningful.

We also have not tested our code transmitting across the mqtt bridge but it works with Elise’s transmitting to self.

import time
import math
import board
import pwmio
from adafruit_circuitplayground import cp
from adafruit_motor import servo

# ----------------------------------------------------------------
# Initialize hardware.

# Create a PWMOut object on pad SDA A5 to generate control signals.
pwm = pwmio.PWMOut(board.A5, duty_cycle=0, frequency=50)

# Create a Servo object which controls a hobby servo using the PWMOut.
actuator = servo.Servo(pwm, min_pulse=1000, max_pulse=2000)

phase_angle = 0.0
phase_rate  = 2*math.pi / 6.0  # one cycle per six seconds, in radians/second
next_servo_update = time.monotonic_ns()
next_status_update = time.monotonic_ns()

while True:
    now = time.monotonic_ns()
    
    if cp.loud_sound():
        actuator.angle = 0
        cp.pixels.fill((255, 0, 0))
        cp.play_tone(1000,.2)
        cp.play_tone(1200, .2)
        cp.play_tone(1400, .2)
        time.sleep(10)

    elif now >= next_servo_update:
        cp.pixels.fill((0, 255, 0))
        next_servo_update += 20000000  # 20 msec in nanoseconds (50 Hz update)
        actuator.angle = 90 + 90 * math.sin(phase_angle)
        phase_angle += phase_rate * 0.020

    # If the time has arrived to display the status:
    if now >= next_status_update:
        next_status_update += 500000000  # 0.5 sec in nanoseconds (2 Hz update)
        print(actuator.angle)