PanCap

Varun Gadh, Hang Wang

02-19-2018

Please find our video here.

Abstract

The initial goal of PanCap was to use motion capture technology to better understand, and digitally simulate, the process of flipping a pancake. We have been able to achieve both of these goals. A tertiary goal – to try to glean information from the Motion Capture that could help teach a robot to flip a pancake – sprung up as a longer-term motivation. This goal is certainly in progress, and understanding the data has helped us narrow down the set of circumstances that will allow a robot pancake flip to occur.

Objectives

Our overarching objective – to better understand and digitally simulate the process of flipping a pancake – broke up into two discrete goals. First, to leverage the position & orientation data capture in the MoCap recordings to find specific border values between each phase of motion of the pancake; this allows us to break up the pancake flip motion into particular physical circumstances. Second, we want to understand more quantitatively what set of skills is necessary to correctly flip a pancake. This could extend to understanding the physical realities of the flip with the potential end goal/motivation being a robotic pancake flip. We would need to and understand the breadth of design that could achieve this goal.

Implementation

 

Outcomes

Likely as a result of the nature of the testing and placement of the markers, in the flip we chose to analyze, one marker position disappears from the data at one particular moment. The process of correcting this data required us to understand the data output format in a greater degree of depth than anticipated. Additionally, in order to correct for noise/inaccuracy, exponential smoothing functions were applied to the proper variable, first derivative, and second derivative values before graphing. Finally, for graphing purposes, the change in values along the axis perpendicular to the “up” and “forward” motions (in the imaginary plane of the pan’s motion) were ignored.

The raw data collected, the digital simulations, and the finite difference results teamed up to allow us to generate a more complex physical understanding of the flip. The process of flip can be broken up into five distinct physical stages:
1) Pan and pancake are still relative to ground
2) Pan is accelerating forwards (away from flipper) and up (away from ground) relative to ground. Pancake is not moving relative to pan, kept still by force from the pan increasing static friction.
2.5) (This may or may not occur. Not only could there be some degree of variation, but also the data was not conclusive.)  Pan continues to accelerate upwards but accelerates backwards while maintaining a forwards velocity. This breaks the static friction between the pancake and the pan.
3) Pan is accelerating downwards and accelerating backwards. Pancake begins to leave pan. Theoretically, this could be over an infinitesimal period However, in practicality there may be some period in which the pan and the pancake remain roughly together, potentially due to surface adhesion or flexibility on the part of the pancake combined with slow downward acceleration on the part of the pan.
4) Pan moves wherever it needs to (typically forwards) to catch the pancake. Pancake is in projectile regime of motion.
5) Pancake and pan collide.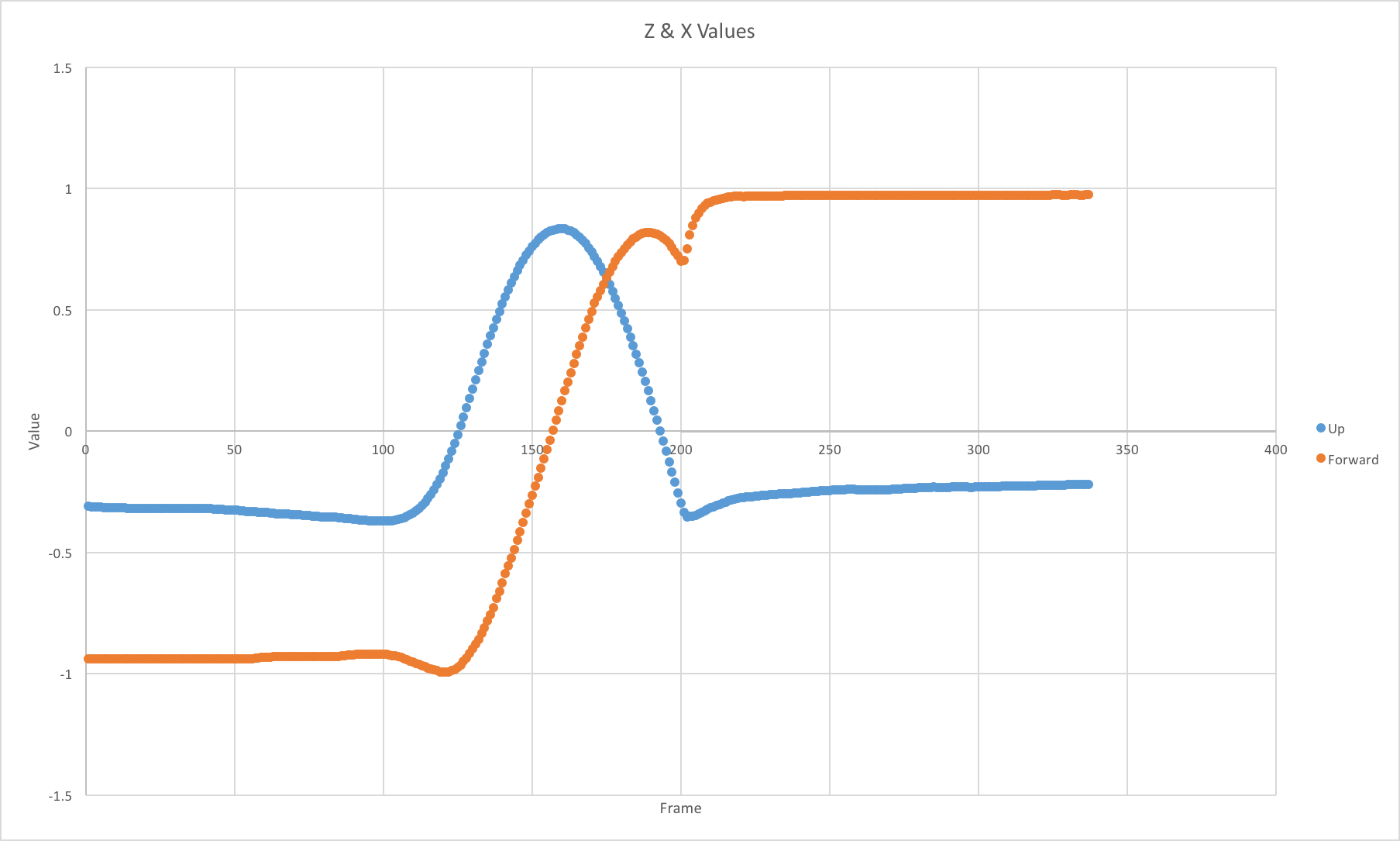
Vertical and forward values of the pancake over frames.

Contribution

-Hang: Grasshopper, animations, videos, original data, co-expert

-Varun: Correcting data, graphs, physical analysis, co-expert

 

Video