Arrows in computing

Modern digital computers were originally developed to simplify, speed up, and remove sources of error from relatively simple, repetitive mathematical operations. (Reductively: engineers were getting frustrated having to spend hours repeatedly solving particular classes of mathematical problems, and figured there must have been some way of mechanizing the process.) Some of the first electronic computers were, fundamentally, no more than a sort of calculator which could remember and refer back to prior results to use in future calculations in a carefully predefined way. At this point in their history, computers were simple, transparent, and “special-purpose,” in the sense that they were designed specifically to solve particular well-defined problems. For instance, an early computer would multiply two complex numbers (which exist in the form a+bi, where i is the imaginary number which is the square root of –1) and return the result; it could do nothing else.

At the early stages of development, the operation of the computing machine may not have been trivially simple, insofar as an uninitiated person may not have been able to intuit their way into getting an answer. But once the general rule of operation was explained to them, a typical user would have been able to begin using the machine quickly, and understand the underlying principle easily enough. In the case of the complex number adding machine referred to above, the user might “dial in” four total values representing a and b from two different complex numbers, press a button, and wait for 30 seconds while the machine hummed along, finally turning numbered rotors to represent the mathematical product.

A great early insight, arrived at in the 1830s but not realized in practice until a century later, profoundly changed the field of computer science. moving it far beyond these “special-purpose” devices. Charles Babbage, working with Ada, the Countess of Lovelace, developed a plan for an Analytical Engine, a machine which could not only perform fixed mathematical operations but also was “programmable”—in other words, it would be able to be modified on the fly to perform different functions, in different orders. It’s difficult to overstate the importance of this leap from a fixed-use mathematical solving machine to one which can be coerced (programmed) to produce different sorts of outcomes from the same input.

Lady Lovelace also contributed enormously to the field with her insight that a computer “might act upon other things besides number,” which was the first known conceptualizing of the expansion of a computer’s power beyond the merely mathematically computational. With this, she allowed for an entirely different class of “arrows” to come into being; if non-numerical entities could be represented, and calculated, stored, etc., then the whole world may potentially be the arrow that any particular piece of a computer’s memory points towards.

Compilers

At the same time that the ability to program computers introduced a new era of possibility, it also brought with it enormous complexity. Remapping the logical operations of a computer was a very difficult and error-prone task; fundamentally, the computer programmer needed a precise and intimate understanding of the computer’s method of operation to be able to write instructions for it which would result in a successful outcome. Early computer instructions, furthermore, were written directly in binary, which certainly does not lend itself to easy understanding or legibility. Generally, a program written to run on one model of computer would likely not run on a different one because of underlying differences in hardware.

In the nineteen fifties, people began to develop compilers (the coinage is from Grace Hopper, a computer pioneer), which were computer programs which could take instructions written by people in a fairly generic form and convert them into programs that would actually run on different pieces of computer hardware. The compiler’s role is to interpret a piece of software and correctly interpret the author’s intent, capturing it in a set of formal instructions applicable to a particular type of hardware.

A compiler represents a sort of indirection (or arrow) which points from the programmer’s language to the “machine code” which will actually be executed by the computer. As “higher-level” computer languages were developed, the gap between the programmer’s original instructions and the underlying machine code grew. Instead of writing the fairly confusing  MOVL $-0x8(%rpb), 0x4A, a programmer might now be able to write something more legible like x = 74; in both cases, the purpose is to set a variable to have the value of 74.

There are more layers here, though. Without entering too much technical detail, it should be sufficient to note that the actual sequence of going from a programmer’s instruction to an underlying behavior in the computer is not so simple as programmer–compiler–machine code; there are other intermediate steps involving further indirection, “linking,” and interpretation along the way. Once the instructions are in machine code, there is still interpretation done by the microcontroller, using yet another type of code called “microcode,” which provides further indirection when the code actually runs.

An example from the Arduino

If you wish to blink an LED on pin 13 of the Arduino, which is the typical point of entry to the hardware platform for new learners, you might run this bit of code:

void setup(){ 
    pinMode(13, OUTPUT);
} 

void loop(){ 
    digitalWrite(13, HIGH); 
    delay(1000); 
    digitalWrite(13, LOW); 
    delay(1000); 
}

This is written in C. But what does the Arduino actually run? A generated hexadecimal file, which looks like this:

:100230000FB60F9211242F933F938F939F93AF93F9
:10024000BF938091010190910201A0910301B091AF
:1002500004013091000123E0230F2D3720F4019693
:10026000A11DB11D05C026E8230F0296A11DB11DD9
:10027000209300018093010190930201A093030158

These are lines 36 to 40 of the code; it is 60 lines long. Here we have seen the two endpoints of the process, from highest-level to lowest-level. To see the indirection and reinterpretation in the midst of them we might examine something as simple as digitalWrite(), the command which turns a pin’s electrical output on or off. When the user asks the Arduino integrated development environment to push their code to the board, it goes through many sequential steps, and one of them is finding and interpreting the definition of digitalWrite(), which is:

void digitalWrite(uint8_t pin, uint8_t val)
{
    uint8_t timer = digitalPinToTimer(pin);
    uint8_t bit = digitalPinToBitMask(pin);
    uint8_t port = digitalPinToPort(pin);
    volatile uint8_t *out;

    if (port == NOT_A_PIN) return;
    // If the pin that support PWM output, we need to turn it off
    // before doing a digital write.
    if (timer != NOT_ON_TIMER) turnOffPWM(timer);

    out = portOutputRegister(port);
    uint8_t oldSREG = SREG;
    cli();

    if (val == LOW) {
        *out &= ~bit;
    } else {
        *out |= bit;
    }
SREG = oldSREG;
}

If this definition is longer and more complex than we might expect, it at least illustrates that the command is simply an on/off switch. And it itself rests on many other definitions; NOT_A_PIN, for instance, is just a variable storing the number 0. HIGH, similarly, is merely a word pointing to the number 1. And ultimately every time any number is stored or referred to on a computer, it itself is simply a series of tiny transistors which are either on or off. Abstractions built upon abstractions built upon abstractions!

To peek into another layer: the first few lines of the Arduino’s assembler version of the digitalWrite() command, for instance, look like this:

 234: 56 ea        ldi r21, 0xA6 ; 166
 236: e5 2e        mov r14, r21
 238: 50 e0        ldi r21, 0x00 ; 0
 23a: f5 2e        mov r15, r21

This is the penultimate level of proximity to the hardware; these assembly code instructions are (in a slightly simplified sense) turned into a part of the hexadecimal machine code shown earlier. Any microcontroller has a list of “opcodes,” i.e. operation codes, particular to it. These are often represented as three- or four-letter acronyms to help the human programmers who are using them, but in yet another indirection, the opcodes written in letters are themselves referring to a purely numerical value; for instance, ADD (“add without carry,” a basic process of addition) is represented by opcode 000011. The ATMega328 has a list of about 100 such codes that will work on that hardware.

Emergent complexity

Obviously computers are capable of undertaking truly complex tasks at high speed. But underlyingly, the complexity and behavior they exhibit is composed entirely of a carefully choreographed interplay of many, many small, simple elements of information, called bits. Each little transistor, following a well-defined rule of electrical behavior, can be said to be a very small cog in a very large machine (for instance, the Atmel chip driving the Arduino Uno has perhaps a million or so).

In the natural world there are myriad examples of individual decisionmaking elements working together in such a way that the complexity of the whole is significantly greater than the parts combined. Consider the flocking behavior of birds or fish; each animal can be modeled as following a simple set of rules regarding their own movement with respect to their peers. When the whole group follows such a set of rules, incredible larger-scale complexity emerges.

Order can emerge from the “decisions” or behaviors of small individually mobile elements in many cases, even when there is seemingly no decision-making life present; regular, periodic sand waves on a beach are merely the result of countless grains which have fallen into a large-scale order, a result of their individual and collective response to wind patterns. On a larger scale, given the right conditions, sand will form into dunes that are hundreds of feet tall.

In addition to the many naturally-occurring examples, we may contrive artificial systems which explore the results of many individually-acting elements sharing a common environment. For one, it’s remarkable how much a “flock” of artificial animals, driven by just three parameters (cohesion, alignment, and separation), bears at least strong superficial similarity to the movement of their natural analogs. A different sort of system can be modeled where each member of a two-dimensional grid has some awareness of the cells around it, and responds accordingly to them; this was explored most famously by John Conway, in his Game of Life.

It is tempting, in any case, to relate the complex behavior of many small individual elements to our own brains, which are, after all, composed merely of many, many individual neurons, attached to each other in a complex web from which our consciousness arises.

Assignment

Build a

which

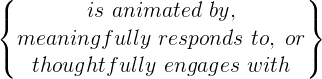
one or more of this unit’s concepts of interest: 

• The layers of direction and indirection used to help humans write machine-processable instructions (such as a program compiler which reads a C program and converts it into assembly language);
• The layering of abstraction upon abstraction as a timesaver and/or confounder and/or transformative force; or 
• The emergence of complex macro-level effects from many individually functioning simple micro elements that behave in concert.

The piece should have a physical manifestation, though it is acceptable for much of the creative work to be developed in software.  It is also acceptable for the piece to be purely mechanical—after all the first computers were simply mechanisms.

Also consider…

• Audience: Who is this piece for? 
• Site specificity: Where will the piece live and why? Will your piece be static or roaming? 
• Performance: Consider how performance relates to the interactivity of your piece. Is your piece a solo performance, collaboration, and/or does it rely on audience interactivity to function (the performance of the machine)?
• Materials: What materials will you use to build your piece? Why those materials and not others? How do your material choice impact the meaning of your project? 

Materials needs

We are able to allocate course budget for purchasing materials for your project needs; please fill out the Course Purchase Request Form as soon as you have certainty about what material(s) you’ll need so that we can place orders with plenty of lead time!

Important Dates

Friday, Nov 8 – Visit the MuseumLab 5:00 – 6:30 p.m.

• All courses involved in the end-of-semester performance and exhibit will be visiting the MusuemLab this Friday, November 8 from 5:00 – 6:30 p.m.
• A note from Zena Ruiz –
  • Feel free to give my google number out to students to schedule another time to visit: 920-320-9795
  • I’m at the museum Tuesday – Saturday 9:00 a.m. – 5:00 p.m. (with the exception of Nov 9 & 23).

Tues, November 12 – Two Project Ideas are DUE

Prepare two distinct project ideas to turn in during class. Please turn these in on clean sheets of 8-1/2″ x 11″ paper. You may want to consider making copies before you turn these in.

EACH PROJECT IDEA SHOULD INCLUDE:

1. A page-length (~300 word) narrative description addressing:

1. 1. 1. 1. Intended interaction mode by members of the public and/or performers and/or yourself (whatever is appropriate to the piece)
         2. Intended siting (where will it live and how will it be installed?)
         3. Intended experience for the audience
         4. Theoretical underpinnings (e.g. what led you to this idea, what about it intrigues you, etc.)
         5. Relevance to you and your practice
2.  At least three drawings showing the proposed build (drawings need not be high-fidelity; sketches are fine)
3. Basic listing of needed materials as well as sources (on or off campus) for those materials (this need not be a finalized purchase list!)

We will review your proposals with you individually.

Thurs, November 14 – Emergent Complexity

Tues, November 26 – Prototype CRITIQUE

You will present a prototype in class for critique that will help you move forward thoughtfully toward the final goals of your project.

• Create a behaves-like prototype: that is to say, an experience prototype for interaction(s). It may have tethers instead of being wireless, or be built larger than the proposed final size, but the fundamental user interactions should be well-modeled. To be quite explicit: the experience that a person has using this prototype should be the same as the experience that person would have using the final piece.
• Write a sample project statement that helps contextualize your prototype and future piece.

We will critique the prototypes in class. This deadline is meant to help you prepare to deliver a finished project a week and a half later.

Practice, Practice, Practice

Thurs, December 5 – Project No. 3 DUE + CRITIQUE

Thurs, December 12 – MuseumLab Pre-installation

• This will likely be after 7:00 p.m., but more details will be announced soon.

Fri, December 13 – MuseumLab Exhibit

Tentative Schedule for day of performance:

• 1:00 p.m. Load materials on a box truck to deliver at the MuseumLab
• 2:30 p.m. Unload materials at the MuseumLab
• 3:00 p.m. – 7:00 p.m.  Begin Install at MuseumLab
• 6:30 p.m.  Dinner on site
• 7:15 p.m. Group Meeting
• 7:45 p.m. Doors Open
• 8:00 – 9:30 p.m. P E R F O R M A N C E
• 9:30 – 11:00 p.m. Strike set, load truck, deliver materials to campus

Mon, December 16 – Documentation is DUE for Project No. 3 at NOON

What to submit (documentation content requirements)

If you have any questions about the submissions requirements, or run into technical problems, be sure to contact either Heidi or Zach.

Each documentation submission must consist of at least:

• A “featured image” that is a good overall view of the project. This image should be one of the “well-shot” images described below, or a cropped subset of one of them.
• The project title.
• Careful and well-shot images of the final project. Take these using IDeATe’s PhotoZone backdrop and lighting for an especially easy professional look, or shoot out in the field if you prefer. The DSLR photography guide provides a lot of pointers.
  Submit at least seven shots and these must include:

1. Overall photo for proportion and scale
2. Detail photo of any part that you’d like to highlight (up to 3)
3. Gif or gifv or little .mov that shows the piece working (i.e. interacting with an input(s) and the output(s) that are derived.)

• Simple narrative description of the thing and usual operation of the thing—the type of plain and straightforward description that you might write in a letter to a child to explain what you had made. Free of judgment and totally literal and straightforward. Try to use as little technical language as possible. (E.g. “A white plastic box has a switch on the top side. When he user turns it on, a green LED flashes five times showing that the system is ready. A small white flag waves back and forth.”) For a study in the art of using simple language, see Randall Munroe’s wonderful Up Goer Five. To use a simple-language filter yourself, try the Up-Goer Five text editor.
• Five progress images, each of which could be a step or misstep that happened along the development process, and each with at least a sentence or two caption. These images may capture decision points, especially interesting or illustrative mistakes, or other mileposts along the way. The idea is that these medium-quality images (though good pictures work too) are taken along the way to document progress. Sometimes you might understand these as being moments-that-matter only in retrospect! The safe route, therefore, is to snap lots of photos as you go along for later review.
• Process Reflection pertaining to process and outcome. For instance, what was easy, what was hard, what did you learn? What little tweak, in retrospect, would’ve changed the direction entirely? This is an opportunity for you to reflect on your creative and technical growth through the project, and think about what growth you want to aim for next. This shouldn’t be a recital of your process, but rather a meaningful consideration of what you experienced during the creation of your piece, 2–4 paragraphs in length.
• Logic Schematic, neatly hand-drawn and scanned, or executed in software like draw.io, Illustrator, or any other way that produces a reasonably legible output. This should be done well enough that a competent person, reading the drawing and with the appropriate parts, could recreate the electrical system of the project.
• Code submission (if using Arduino), embedded into the project page, and optionally also with a Github or other version control service public-facing link. Your code should be reasonably commented throughout so that people other than you (the author) can better understand it. You don’t need to explain every single line—that would be overkill—but leave useful notes in a reasonable measure. Write a comment block at the top of the code including:
  • the project title,
  • (optionally) your name,
  • a description (short or long) of what the code does,
  • any description of pin mapping that would be useful to somebody else trying to recreate your work,
  • appropriate credit to any other person’s/project’s code that you incorporated into your project, and
  • (optionally) a license notice (i.e. copyright, CC BY-SA 4.0, the MIT License, release it to the public domain, or just follow your heart). If you have written code that you wish to keep strictly proprietary for any reason, please speak with the instructor about an exception to this documentation requirement.

How to submit (WordPress instructions)

All documentation is submitted by making a post on the course site.

• Make a post with the title in the format “Project no. 1: Your Project’s Name Here.” On the right side of the page where you compose your post, under “Categories” select “Project no. 1.”
• Upload your images at a reasonably high resolution; ~1000 pixels of width is the lower boundary of what you should aim for. After adding an image to the post, click on it in the editor, click on the pencil icon to get to its Image Details popup, and select Size: large or Size: original.
• You can also use the Image Details menu to add a caption to an image.

Grading scheme

• 6% Initial ideation
• 4% Emergent Complexity Exercise + Reading
• 20% Prototype critique
• 50% Final critique + Project Sharing
• 20% Final documentation

Extra credit

The final critique for this project in on Thursday, December 5. At that time, all projects will be evaluated and critiqued to a final standard. There is another subsequent performance/showing opportunity for the project, at the MuseumLab show which is 8 days later on December 13th. In most cases, we expect students will show their work at the Museum in the same form it appeared at the final critique; however, given that there’s a significant gap between the two deadlines, there is an opportunity for improvement.

You will get your Project 3 final critique grade on Friday, December 6. If you are dissatisfied with your grade, and/or wish to further develop Project 3 for regrading at the time of the MuseumLab performance, you should talk with Heidi and Zach as early as possible so that we can discuss what change(s) you’re planning to effect and be sure we’re on the same page.

Additionally, if you wish to meaningfully change your Project 1 or Project 2 piece for inclusion in the MuseumLab show, those are also fair game for regrading, based on the pieces as shown on December 13 at the Museum. In all cases, the original grade will be averaged with the newly assigned grade to form a new final grade for the piece.