Double Pendulum Simulator¶
The double pendulum simulator demonstrates the dynamic simulation and control of a two-link arm. Without joint torques, it is a chaotic double-pendulum system, but with control torques applied, it is a limitless two-link arm in a vertical plane.
The simulator is written in Python 3 using PyQt5 for the user interface. Each exercise has specific demo code and the library packaged as a single file:
Contents
Requirements¶
The code requires a working installation of Python 3 with PyQt5, scipy, numpy, and pyqtgraph. On an IDeATe cluster MacBook Pro, you will need to use the specific installation of Python 3 which includes the required libraries. The simulator scripts can be run from the Terminal command line on an IDeATe cluster MBP as follows:
/opt/local/bin/python3.5 dblpend_free.py
/opt/local/bin/python3.5 dblpend_keyframes.py
/opt/local/bin/python3.5 dblpend_swingup.py
A README.txt file is included in the zip with more detailed launching instructions.
Script Examples¶
The simulator library module rcp.ex.dblpend provides a common GUI
framework with a graphic cartoon, phase plot, text display, and general-purpose
parameter sliders. The top-level scripts all share this module but add a
specific control function to execute a movement. Following are several sample
scripts highlighting different approaches. The underlying numerical code can be
found in rcp.doublependulum.
Free Motion Script¶
The ‘free motion’ demo applies zero torques to show the natural dynamics of a
chaotic double pendulum. The script subclasses
rcp.doublependulum.DoublePendulumController to provide a custom
control method, then passes the class itself into the application framework.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 | #!/usr/bin/env python3
"""Prototype Python 3 script for the 16-375 double-pendulum control exercise."""
################################################################
# Written in 2018-2019 by Garth Zeglin <garthz@cmu.edu>
# To the extent possible under law, the author has dedicated all copyright
# and related and neighboring rights to this software to the public domain
# worldwide. This software is distributed without any warranty.
# You should have received a copy of the CC0 Public Domain Dedication along with this software.
# If not, see <http://creativecommons.org/publicdomain/zero/1.0/>.
################################################################
import rcp.doublependulum
from rcp.ex.dblpend import main
import numpy as np
################################################################
class PendulumController(rcp.doublependulum.DoublePendulumController):
def __init__(self):
super().__init__()
# override the default initial state
self.initial_state = np.array([3.0, 0.0, 0.0, 0.0])
return
#================================================================
def setup(self):
self.write("""Passive double-pendulum simulation.
A zero torque vector is applied to the joints so they swing freely. The underlying simulation has frictionless joints so the behavior is chaotic. It is ultimately unstable due to accumulated numerical error.\n""")
return
#================================================================
def compute_control(self, t, dt, state, tau):
"""Method called from simulator to calculate the next step of applied torques.
:param t: time in seconds since simulation began
:param state: four element numpy array with joint positions ``q`` and joint velocities ``qd`` as ``[q0, q1, qd0, qd1]``, expressed in radians and radians/sec
:param tau: two element numpy array to fill in with the joint torques to apply ``[tau0, tau1]``
"""
tau[0:2] = (0,0)
# temporary kinematics test
# elbow, end = self.model.forwardKinematics(state[0:2])
# s1, s2 = self.model.endpointIK(end)
# print("q:", state[0], state[1], "elbow:", elbow, "end:", end, "solution1: ", s1, "solution2:", s2)
# print("q:", state[0], state[1], "end:", end, "solution1: ", s1, "solution2:", s2)
return
################################################################$
if __name__ == "__main__":
main(PendulumController)
|
Keyframed Motion Demo Script¶
The ‘keyframed motion’ demo applies position control using a short looped sequences of reference poses.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 | #!/usr/bin/env python3
"""Prototype Python 3 script for the 16-375 double-pendulum control exercise."""
################################################################
# Written in 2018-2019 by Garth Zeglin <garthz@cmu.edu>
# To the extent possible under law, the author has dedicated all copyright
# and related and neighboring rights to this software to the public domain
# worldwide. This software is distributed without any warranty.
# You should have received a copy of the CC0 Public Domain Dedication along with this software.
# If not, see <http://creativecommons.org/publicdomain/zero/1.0/>.
################################################################
import math
import numpy as np
import rcp.doublependulum
from rcp.ex.dblpend import main
################################################################
class PendulumController(rcp.doublependulum.DoublePendulumController):
def __init__(self):
super().__init__()
# for this example, there are four fixed poses commanded a fixed intervals, expressed as a set of (q0, q1) pairs
self.keyframes = np.zeros((4,2))
self.last_frame = None
return
#================================================================
def setup(self):
self.write("""Keyframed position control demonstration.
Applies a sequence of joint targets to a position controller at fixed intervals.
The parameter sliders 0 and 1 control the 'shoulder' and 'elbow' angles for the first keyframe, 2 and 3 are the second keyframe, etc.
""")
return
#================================================================
def user_parameter_change(self, parameter, value):
pose = parameter // 2
joint = parameter % 2
if pose < len(self.keyframes):
self.keyframes[pose][joint] = 2 * math.pi * (value - 0.5)
self.write("Set pose %d joint %d to angle %f" % (pose, joint, self.keyframes[pose][joint]))
def apply_configuration(self, config):
if 'keyframes' in config:
for i in range(len(self.keyframes)):
q0 = config['keyframes'].getfloat('keyframe-%d-q0' % i, fallback = 0.0)
q1 = config['keyframes'].getfloat('keyframe-%d-q1' % i, fallback = 0.0)
self.keyframes[i,:] = [q0, q1]
return
def gather_configuration(self, config):
if 'keyframes' not in config:
config['keyframes'] = {}
for i in range(len(self.keyframes)):
config['keyframes']['keyframe-%d-q0' % i] = str(self.keyframes[i, 0])
config['keyframes']['keyframe-%d-q1' % i] = str(self.keyframes[i, 1])
return
#================================================================
def compute_control(self, t, dt, state, tau):
"""Method called from simulator to calculate the next step of applied torques.
:param t: time in seconds since simulation began
:param state: four element numpy array with joint positions ``q`` and joint velocities ``qd`` as ``[q0, q1, qd0, qd1]``, expressed in radians and radians/sec
:param tau: two element numpy array to fill in with the joint torques to apply ``[tau0, tau1]``
"""
# select the current keyframe based on the time
frame = int(t // 1.5)
if frame != self.last_frame:
self.write("Starting frame %d" % frame)
self.last_frame = frame
# select the pose for the current keyframe, looping over the available poses
pose = self.keyframes[frame % len(self.keyframes)]
# create a target state by extending the pose to include velocity
target = np.concatenate((pose, np.zeros(2)))
# calculate position and velocity error as difference from reference state
qerr = target - state
# apply PD control to reach the pose (no integral term)
tau[0] = (self.kp[0] * qerr[0]) + (self.kd[0] * qerr[2])
tau[1] = (self.kp[1] * qerr[1]) + (self.kd[1] * qerr[3])
return
################################################################$
if __name__ == "__main__":
main(PendulumController)
|
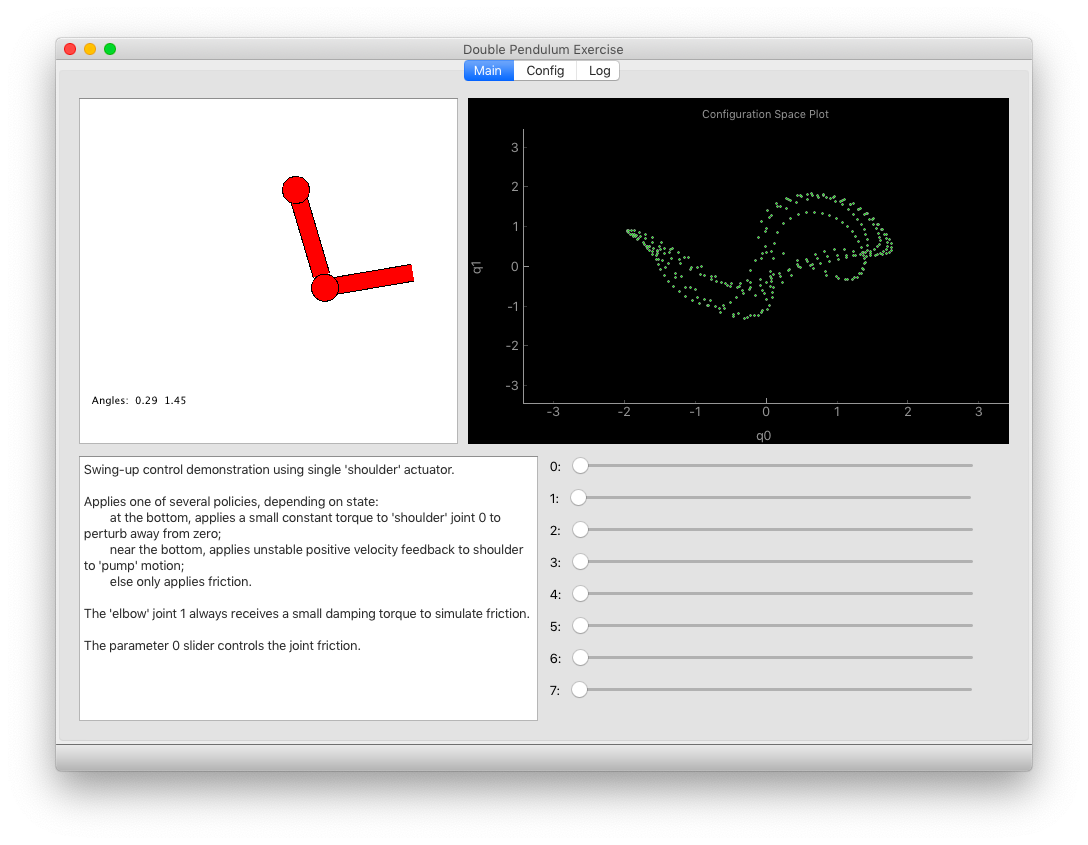
Swing-up Demo Script¶
The ‘swingup’ demo applies position control using a short looped sequences of reference poses.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 | #!/usr/bin/env python3
"""Prototype Python 3 script for the 16-375 double-pendulum control exercise."""
################################################################
# Written in 2018-2019 by Garth Zeglin <garthz@cmu.edu>
# To the extent possible under law, the author has dedicated all copyright
# and related and neighboring rights to this software to the public domain
# worldwide. This software is distributed without any warranty.
# You should have received a copy of the CC0 Public Domain Dedication along with this software.
# If not, see <http://creativecommons.org/publicdomain/zero/1.0/>.
################################################################
import math
import numpy as np
import rcp.doublependulum
from rcp.ex.dblpend import main
################################################################
class PendulumController(rcp.doublependulum.DoublePendulumController):
def __init__(self):
super().__init__()
# for this example, there are four fixed poses commanded a fixed intervals, expressed as a set of (q0, q1) pairs
self.keyframes = np.zeros((4,2))
self.last_frame = None
return
#================================================================
def setup(self):
self.write("""Keyframed position control demonstration.
Applies a sequence of joint targets to a position controller at fixed intervals.
The parameter sliders 0 and 1 control the 'shoulder' and 'elbow' angles for the first keyframe, 2 and 3 are the second keyframe, etc.
""")
return
#================================================================
def user_parameter_change(self, parameter, value):
pose = parameter // 2
joint = parameter % 2
if pose < len(self.keyframes):
self.keyframes[pose][joint] = 2 * math.pi * (value - 0.5)
self.write("Set pose %d joint %d to angle %f" % (pose, joint, self.keyframes[pose][joint]))
def apply_configuration(self, config):
if 'keyframes' in config:
for i in range(len(self.keyframes)):
q0 = config['keyframes'].getfloat('keyframe-%d-q0' % i, fallback = 0.0)
q1 = config['keyframes'].getfloat('keyframe-%d-q1' % i, fallback = 0.0)
self.keyframes[i,:] = [q0, q1]
return
def gather_configuration(self, config):
if 'keyframes' not in config:
config['keyframes'] = {}
for i in range(len(self.keyframes)):
config['keyframes']['keyframe-%d-q0' % i] = str(self.keyframes[i, 0])
config['keyframes']['keyframe-%d-q1' % i] = str(self.keyframes[i, 1])
return
#================================================================
def compute_control(self, t, dt, state, tau):
"""Method called from simulator to calculate the next step of applied torques.
:param t: time in seconds since simulation began
:param state: four element numpy array with joint positions ``q`` and joint velocities ``qd`` as ``[q0, q1, qd0, qd1]``, expressed in radians and radians/sec
:param tau: two element numpy array to fill in with the joint torques to apply ``[tau0, tau1]``
"""
# select the current keyframe based on the time
frame = int(t // 1.5)
if frame != self.last_frame:
self.write("Starting frame %d" % frame)
self.last_frame = frame
# select the pose for the current keyframe, looping over the available poses
pose = self.keyframes[frame % len(self.keyframes)]
# create a target state by extending the pose to include velocity
target = np.concatenate((pose, np.zeros(2)))
# calculate position and velocity error as difference from reference state
qerr = target - state
# apply PD control to reach the pose (no integral term)
tau[0] = (self.kp[0] * qerr[0]) + (self.kd[0] * qerr[2])
tau[1] = (self.kp[1] * qerr[1]) + (self.kd[1] * qerr[3])
return
################################################################$
if __name__ == "__main__":
main(PendulumController)
|
Dual-Robot Free Swing¶
The two-pendulum ‘free’ demo applies zero torques using a pair of double-pendula to show the natural dynamics from slightly different initial conditions.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 | #!/usr/bin/env python3
"""Prototype Python 3 script for the 16-375 double-pendulum control exercise."""
################################################################
# Written in 2018-2019 by Garth Zeglin <garthz@cmu.edu>
# To the extent possible under law, the author has dedicated all copyright
# and related and neighboring rights to this software to the public domain
# worldwide. This software is distributed without any warranty.
# You should have received a copy of the CC0 Public Domain Dedication along with this software.
# If not, see <http://creativecommons.org/publicdomain/zero/1.0/>.
################################################################
import rcp.doublependulum
from rcp.ex.ndblpend import main
import numpy as np
################################################################
class PendulumController(rcp.doublependulum.DoublePendulumController):
def __init__(self):
super().__init__()
# override the default initial state
self.initial_state = np.array([3.0, 0.0, 0.0, 0.0])
return
#================================================================
# Specialize this particular controller when a member of an ensemble.
def set_identity(self, serial_number):
super().set_identity(serial_number)
# perturb the initial state
self.initial_state[0] += self.identity * 0.05
return
#================================================================
def setup(self):
if self.identity == 0:
self.write("""Passive double-pendulum simulation.
A zero torque vector is applied to the joints so they swing freely. The underlying simulation has frictionless joints so the behavior is chaotic. It is ultimately unstable due to accumulated numerical error.\n""")
return
#================================================================
def compute_control(self, t, dt, state, tau):
"""Method called from simulator to calculate the next step of applied torques.
:param t: time in seconds since simulation began
:param state: four element numpy array with joint positions ``q`` and joint velocities ``qd`` as ``[q0, q1, qd0, qd1]``, expressed in radians and radians/sec
:param tau: two element numpy array to fill in with the joint torques to apply ``[tau0, tau1]``
"""
tau[0:2] = (0,0)
# temporary kinematics test
# elbow, end = self.model.forwardKinematics(state[0:2])
# s1, s2 = self.model.endpointIK(end)
# print("q:", state[0], state[1], "elbow:", elbow, "end:", end, "solution1: ", s1, "solution2:", s2)
# print("q:", state[0], state[1], "end:", end, "solution1: ", s1, "solution2:", s2)
return
################################################################$
if __name__ == "__main__":
main(PendulumController)
|
Dual-Robot Spirals¶
The two-pendulum ‘spirals’ demo uses inverse kinematics to track a spiral with the left arm, using the right arm to track the left.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 | #!/usr/bin/env python3
"""Prototype Python 3 script for the 16-375 double-pendulum control exercise."""
################################################################
# Written in 2018-2019 by Garth Zeglin <garthz@cmu.edu>
# To the extent possible under law, the author has dedicated all copyright
# and related and neighboring rights to this software to the public domain
# worldwide. This software is distributed without any warranty.
# You should have received a copy of the CC0 Public Domain Dedication along with this software.
# If not, see <http://creativecommons.org/publicdomain/zero/1.0/>.
################################################################
import math
import numpy as np
import rcp.doublependulum
from rcp.ex.ndblpend import main
################################################################
class PendulumController(rcp.doublependulum.DoublePendulumController):
def __init__(self):
super().__init__()
self.timestep = 0
# set stiffer position and damping gains
self.kp = np.array((100.0, 50.0))
self.kd = np.array((16.0, 8.0))
return
#================================================================
def setup(self):
if self.identity == 0:
self.write("""Pair of double-pendulum simulations.
One moves the endpoint along a circular path, while the other tries to follow.
""")
return
#================================================================
def compute_control(self, t, dt, state, tau):
"""Method called from simulator to calculate the next step of applied torques.
:param t: time in seconds since simulation began
:param state: four element numpy array with joint positions ``q`` and joint velocities ``qd`` as ``[q0, q1, qd0, qd1]``, expressed in radians and radians/sec
:param tau: two element numpy array to fill in with the joint torques to apply ``[tau0, tau1]``
"""
if self.identity == 0:
# the first robot chooses a target pose in robot coordinates based
# on the inverse kinematics solution for a spiral path
# phase cycles one revolution of the circular path angle every 8 seconds
phase = 0.25 * np.pi * t
# radius slowly cycles up and down again
radius = 0.1 + 0.5 * abs(math.sin(0.05 * t))
# end is the world-coordinate location of a point traveling around the spiral centered between the two arms
end = np.array((1.0 + radius * np.cos(phase), radius * np.sin(phase)))
# solve for the joint angles for the given endpoint
s1, s2 = self.model.endpointIK(end)
# arbitrarily one solution as the target pose
pose = s1
if self.timestep % 1000 == 0:
self.write("Time: %f endpoint: %s" % (t, end))
self.world.set_marker(0, end)
else:
# the other robot observes the first and tries to track the endpoint
end0 = self.world.dblpend_endpoint(0)
s1, s2 = self.model.endpointIK(end0)
pose = s2
# create a target state by extending the pose to include velocity
target = np.concatenate((pose, np.zeros(2)))
# calculate position and velocity error as difference from reference state
qerr = target - state
# apply PD control to reach the pose (no integral term)
tau[0] = (self.kp[0] * qerr[0]) + (self.kd[0] * qerr[2])
tau[1] = (self.kp[1] * qerr[1]) + (self.kd[1] * qerr[3])
self.timestep += 1
return
################################################################$
if __name__ == "__main__":
main(PendulumController)
|