In one of my other courses (Foundations of Intelligent Infrastructure), we went through an exercise today where we recorded sound and then used Matlab to map frequencies.
My group measured the sound of different shoes stomping on the concrete hall in Porter. Graphs showing frequency and sound below.
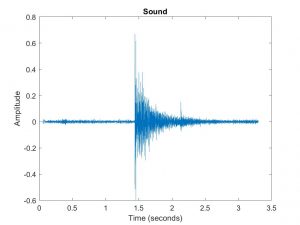
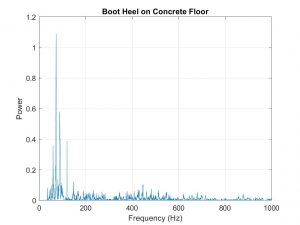
Our experiment reminded the professor of a project at CMU where floor sensors are used to measure movement across spaces. The specific application discussed is in elder care, but also may be a way to provide less invasive monitoring of spaces.
https://www.cmu.edu/piper/news/archives/2017/february/noh-wins-NSF-award.html
https://www.andrew.cmu.edu/user/shijiapa/documentations/Pan_Ubicomp_2017.pdf
Matlab code (note: need to drop sound file into the same folder as the Matlab file):
%%
clear all; clc;
% Load signal in the time domain, x (fs is the sample rate in hertz)
[x,fs] = audioread('takeone.m4a');
tb = (0:1/fs:(length(x)-1)/fs); % Convert samples, k, to time base, t
plot(tb,x)
xlabel('Time (seconds)')
ylabel('Amplitude')
title('Sound')
%%
% Play the sound
sound(x,fs)
%%
% Use the fft command to compute the DFT of the signal.
m = length(x); % Window length, N
y = fft(x,m); % DFT of signal
f = (0:m-1)*(fs/m); % Frequency range
p = y.*conj(y)/m; % Power of the DFT
% Plot up to the Nyquist frequency:
plot(f(1:floor(m/2)),p(1:floor(m/2)))
xlabel('Frequency (Hz)')
ylabel('Power')
title('Five Shoe Stomps on Concrete Floor')
grid on;
xlim([0 1000]) % Zoom in on relevant range