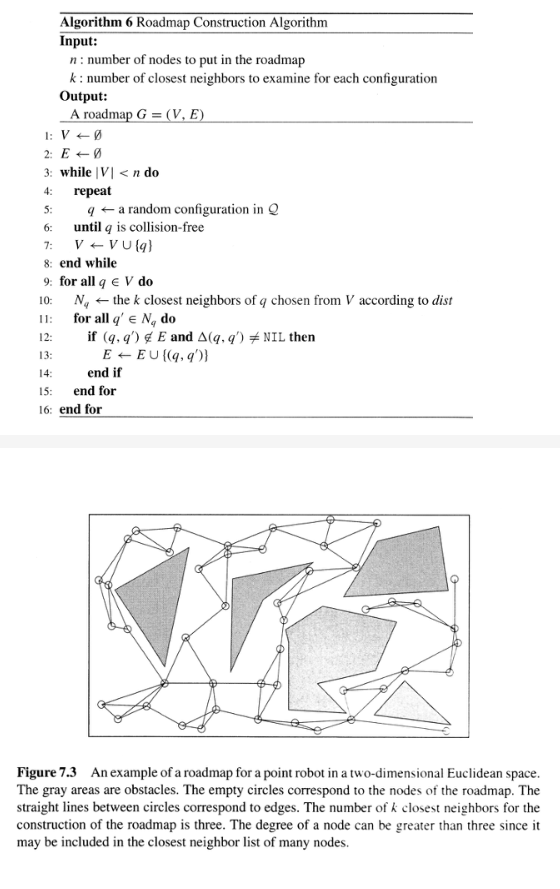
This portrait is based on the idea of the probabilistic road map as described in ‘Probabilistic Roadmap Path Planning’ by H. Choset et al. where the figure in the portrait is graph G and the red background are obstacles/collisions.
Controls
- RIGHT ARROW = advance drawing one step
- ENTER = start & stop drawing
- ‘r’ = refresh
sketch
//Name: Tsz Wing Clover Chau
//andrewid: ctchau
//Section E
//Project 9
var chosenPixels;
var step;
var bgPx = [];
var rStep;
var range = 30;
var baseImage;
function preload(){
baseImage = loadImage("https://i.imgur.com/PaF0PFq.png");
}
function setup(){
createCanvas(480, 480);
background(255);
frameRate(30);
baseImage.loadPixels();
//init array
chosenPixels = [];
bgPx = [];
step = false;
rStep = random(0, 30);
for (var i = 0; i < rStep; i++){
pt = makePoint(int(random(0, 480)), int(random(0, 480)));
if (isRed(pt)) {
bgPx.push(pt);
} else {
chosenPixels.push(pt);
}
}
}
function draw() {
drawBg();
if (keyIsDown(RIGHT_ARROW) || step){ // press right arrow to invidually step
addPx();
}
drawFace();
}
//HELPER FUNCTIONS
function makePoint(px, py){
var pt = {x: px, y: py};
pt.c = baseImage.get(px, py);
pt.neighbors;
return pt;
}
function addPx(){
rStep = random(0, 100);
var newPx = 0;
while (newPx < rStep){
pt = makePoint(int(random(0, 480)), int(random(0, 480)));
//add to bg array + pick new if red
while (isRed(pt)){
if (int(random(0, 8)) == 1){
bgPx.push(pt);
}
pt = makePoint(int(random(0, 480)), int(random(0, 480)));
}
var min_dist = range;
for (var j = 0; j < chosenPixels.length; j++){
var checkPx = chosenPixels[j];
var d = dist(checkPx.x, checkPx.y, pt.x, pt.y);
if ((dist(checkPx.x, checkPx.y, pt.x, pt.y) < range) & (d < min_dist)){
min_dist = d;
stroke(pt.c);
strokeWeight(0.5);
line(checkPx.x, checkPx.y, pt.x, pt.y);
chosenPixels.push(pt);
newPx ++;
break;
}
}
}
}
function isRed(pt){
if (pt.c[0] > 50 & pt.c[1] < 30){
return true;
}
return false;
}
function keyPressed(){
if (keyCode == ENTER){ //ENTER to autocomplete
step = !step;
} else if (key == 'r'){ //press 'r' to reset!
setup();
}
}
function drawBg(){
for (var i = 0; i < bgPx.length; i++){
px = bgPx[i];
px.c[3]= 80;
stroke(px.c);
strokeWeight(0.3);
if (int(random(0,2)) == 1){
line(px.x, 0, px.x, height);
} else {
line(0, px.y, width, px.y);
}
}
}
function drawFace(){
for (var i = 0; i < chosenPixels.length; i++){
var curPx = chosenPixels[i];
stroke(curPx.c);
strokeWeight(5);
point(curPx.x, curPx.y);
}
}
Logic/Pseudocode:
- Configuration q = series of randomly generated non-background pixels (ie. not red).
- Q = new randomly generated non-background pixels
- if distance from q -> Q < acceptable range, append to q
- N = rStep (ie. no. of new non-background pixels added to q)

References:
http://www.cs.columbia.edu/~allen/F15/NOTES/Probabilisticpath.pdf
![[OLD SEMESTER] 15-104 • Introduction to Computing for Creative Practice](wp-content/uploads/2023/09/stop-banner.png)