Category: 03-LineExercises

aahdee – LineExercises

 

Dashed line

Living Line

[videopack id=”773″]https://courses.ideate.cmu.edu/60-428/f2021/wp-content/uploads/2021/09/livingline.mp4[/videopack]

Spicy Line

[videopack id=”778″]https://courses.ideate.cmu.edu/60-428/f2021/wp-content/uploads/2021/09/spicyline.mp4[/videopack]

Circle

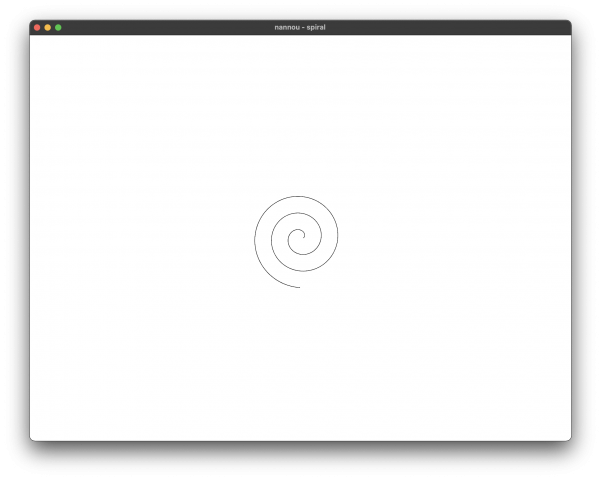
Spiral

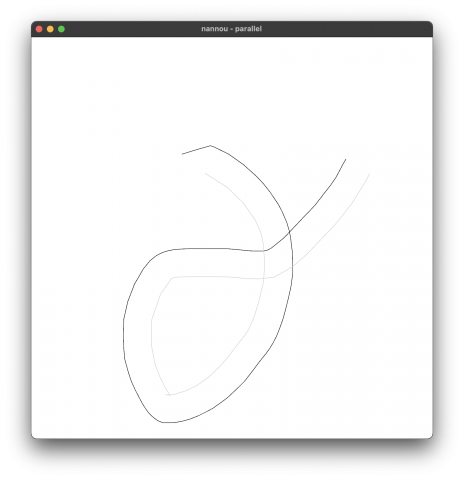
Parallel

[videopack id=”783″]https://courses.ideate.cmu.edu/60-428/f2021/wp-content/uploads/2021/09/DwM_LineExercises-2021-09-14-23-49-37.mp4[/videopack]

Different Weights

Calligraphic

[not an svg – im having some save errors. will add later]

Continue reading “aahdee – LineExercises”

sapeck-LineExercises

A: Dashed Line

/*
* sapeck_03_A_DashedLine.pde
* A dashed line between the center and the mouse
* Originally created by sapeck 2021-09-14
* CMU 60-428 F21 Drawing With Machines
*/

int DASH_INTERVAL = 20;

void setup() {
  size(640, 480);
}

void draw() {
  background(255, 255, 255);
  
  
  float d = dist(width/2, height/2, mouseX, mouseY);
  float num = d/DASH_INTERVAL;
  for (int i = 0; i <= num; i += 2) {
    float x1 = lerp(width/2, mouseX, i/num);
    float y1 = lerp(height/2, mouseY, i/num);
    float x2 = lerp(width/2, mouseX, min(1.0, (i+1)/num));
    float y2 = lerp(height/2, mouseY, min(1.0, (i+1)/num));
    line(x1, y1, x2, y2);
  }
}

void mouseClicked() {
  saveFrame("sapeck_03_A_DashedLine_####.png");
}

B: Living Line

/*
* sapeck_03_B_LivingLine.pde
* A mouse trail
* Originally created by sapeck 2021-09-14
* CMU 60-428 F21 Drawing With Machines
*/

int NUM_POSITIONS = 100;

// Two 2D arrays
ArrayList x_positions = new ArrayList();
ArrayList y_positions = new ArrayList();

// One 2D Array
ArrayList<Integer[]> xy_positions = new ArrayList<Integer[]>();

// One Array of Objects (PVectors)
ArrayList pv_positions = new ArrayList();

void setup() {
  size(640, 480);
}

void mouseMoved() {
  // If there are 100 points recorded, remove the first one
  // This is a FIFO list, so the items are appended to the end
  // and removed from the beginning.
  if (x_positions.size() >= 100) {
    x_positions.remove(0);
    y_positions.remove(0);
    xy_positions.remove(0);
    pv_positions.remove(0);
  }
  
  // Add the new location
  x_positions.add(mouseX);
  y_positions.add(mouseY);
  Integer[] xy = { mouseX, mouseY };
  xy_positions.add(xy);
  PVector pv = new PVector(mouseX, mouseY);
  pv_positions.add(pv);
}

void draw() {
  background(255, 255, 255);
  
  beginShape();
  for (int i = 0; i < pv_positions.size(); i++) {
    // Loop over each item in the list and add a point
    // to the line
    PVector pv = pv_positions.get(i);
    vertex(pv.x, pv.y);
  }
  endShape();
}

void mouseClicked() {
  saveFrame("sapeck_03_B_LivingLine_####.png");
}

C: Spicy Line

/*
* sapeck_03_C_SpicyLine.pde
* A mouse trail that gets spicy
* Originally created by sapeck 2021-09-14
* CMU 60-428 F21 Drawing With Machines
*/

int NUM_POSITIONS = 100;
float RANDOMNESS_START = 1;
float RANDOMNESS_RATE = 0.008;

// One Array of Objects (PVectors)
ArrayList pv_positions = new ArrayList();

float randomness = RANDOMNESS_START;

void setup() {
  size(640, 480);
}

void mouseMoved() {
  // Increase the randomness over time of movements
  randomness += RANDOMNESS_RATE;
  
  // If there are 100 points recorded, remove the first one
  // This is a FIFO list, so the items are appended to the end
  // and removed from the beginning.
  if (pv_positions.size() >= 100) pv_positions.remove(0);
  
  // Add the new location
  float x = mouseX + random(-1 * randomness, randomness);
  float y = mouseY + random(-1 * randomness, randomness);
  PVector pv = new PVector(x, y);
  pv_positions.add(pv);
}

void draw() {
  background(255, 255, 255);
  
  beginShape();
  for (int i = 0; i < pv_positions.size(); i++) {
    // Loop over each item in the list and add a point
    // to the curve
    PVector pv = pv_positions.get(i);
    vertex(pv.x, pv.y);
  }
  endShape();
}

void mouseClicked() {
  saveFrame("sapeck_03_C_SpicyLine_####.png");
}

D: One Circle, Two Ways

Sine and Cosine Points

/*
* sapeck_03_D_OneCircleTwoWays_SINCOSPoints.pde
* A circle made from sine and cosine points
* Originally created by sapeck 2021-09-14
* CMU 60-428 F21 Drawing With Machines
*/

int NUM_POINTS = 20;
float CIRCLE_RADIUS = 100;

// One Array of Objects (PVectors)
PVector pv_positions[] = new PVector[NUM_POINTS];

void setup() {
  size(640, 480);
  
  for (int i = 0; i < NUM_POINTS; i++) {
    float x = CIRCLE_RADIUS * cos(i * (TWO_PI / NUM_POINTS)) + (width / 2); 
    float y = CIRCLE_RADIUS * sin(i * (TWO_PI / NUM_POINTS)) + (height / 2); 
    pv_positions[i] = new PVector(x, y);
  }
}

void draw() {
  background(255, 255, 255);
  
  beginShape();
  for (int i = 0; i < NUM_POINTS; i++) {
    // Loop over each item in the list and add a point
    // to the curve
    PVector pv = pv_positions[i];
    vertex(pv.x, pv.y);
  }
  endShape(CLOSE);
}

void mouseClicked() {
  saveFrame("sapeck_03_D_OneCircleTwoWays_SINCOSPoints_####.png");
}

Cosine and Square Root

/*
* sapeck_03_D_OneCircleTwoWays_SQRT.pde
* A circle made from cosine and square root
* Originally created by sapeck 2021-09-14
* CMU 60-428 F21 Drawing With Machines
*/

int NUM_POINTS = 20;
float CIRCLE_RADIUS = 100;

// One Array of Objects (PVectors)
PVector pv_positions[] = new PVector[NUM_POINTS];

float CIRCLE_RADIUS_SQ = pow(CIRCLE_RADIUS, 2);

void setup() {
  size(640, 480);
  
  for (int i = 0; i < NUM_POINTS; i++) { float x = CIRCLE_RADIUS * cos(i * (TWO_PI / NUM_POINTS)); float x_sq = pow(x, 2); float y = sqrt(CIRCLE_RADIUS_SQ - x_sq); float x_aligned = x + (width / 2); float y_aligned = (height / 2) + y; if (i > NUM_POINTS / 2) y_aligned -= 2 * y;
    pv_positions[i] = new PVector(x_aligned, y_aligned);
  }
}

void draw() {
  background(255, 255, 255);
  
  beginShape();
  for (int i = 0; i < NUM_POINTS; i++) {
    // Loop over each item in the list and add a point
    // to the curve
    PVector pv = pv_positions[i];
    vertex(pv.x, pv.y);
  }
  endShape(CLOSE);
}

void mouseClicked() {
  saveFrame("sapeck_03_D_OneCircleTwoWays_SQRT_####.png");
}

E: Spiral

/*
* sapeck_03_E_Spiral.pde
* A spiral made from a circle with increasing radius
* Originally created by sapeck 2021-09-14
* CMU 60-428 F21 Drawing With Machines
*/

int POINTS_PER_ROTATION = 10;
int NUM_POINTS = 50;
float RADIUS_GROWTH_PER_POINT = 4;

// One Array of Objects (PVectors)
PVector pv_positions[] = new PVector[NUM_POINTS];

float radius = 0;

void setup() {
  size(640, 480);
  
  for (int i = 0; i < NUM_POINTS; i++) {
    float theta = i * (TWO_PI / POINTS_PER_ROTATION);
    float x = radius * cos(theta) + (width / 2);
    float y = radius * sin(theta) + (height / 2);
    pv_positions[i] = new PVector(x, y);
    radius += RADIUS_GROWTH_PER_POINT;
  }
}

void draw() {
  background(255, 255, 255);
  
  beginShape();
  for (int i = 0; i < NUM_POINTS; i++) {
    // Loop over each item in the list and add a point
    // to the curve
    PVector pv = pv_positions[i];
    curveVertex(pv.x, pv.y);
  }
  endShape();
}

void mouseClicked() {
  saveFrame("sapeck_03_E_Spiral_####.png");
}

F: Parallel Polyline

For this one, I used vsketch, vpype, and shapely. It’s as simple as installing these Python packages and then running “vsk run” and it will bring a viewer, auto-reload your code, and save an SVG for you when you click the “LIKE!”button.

#!/usr/bin/env python3
#
# sapeck_03_F_ParallelPolyline.py
# Draw a teardrop-like shape with inner and outer offset lines
# Originally created by sapeck 2021-09-15
# CMU 60-428 F21 Drawing With Machines
#

from math import cos, sin

from shapely.geometry import LineString, MultiLineString
import vsketch

PI = 3.14159

class Sapeck03FParallelpolylineVskSketch(vsketch.SketchClass):
    CIRCLE_POINTS = 100
    RADIUS = 2

    def draw(self, vsk: vsketch.Vsketch) -> None:
        vsk.size("letter", landscape=False)
        vsk.scale("in")

        # This makes a teardrop-like shape
        points = [(0, 0)]
        for i in range(0, self.CIRCLE_POINTS):
          x = self.RADIUS * cos(i * (PI / self.CIRCLE_POINTS))
          y = self.RADIUS * sin(i * (PI / self.CIRCLE_POINTS)) + self.RADIUS + 1
          points.append((x, y))
        points.append((0, 0))
        
        # points is just an array of (x, y) points
        line = LineString(points)
        vsk.stroke(1)
        vsk.geometry(line)
        
        # Now make the inner and outer offsets
        vsk.stroke(2)
        offset0 = line.parallel_offset(1, 'left',  join_style=2, mitre_limit=10.0) # inner offset
        offset1 = line.parallel_offset(1, 'right', join_style=2, mitre_limit=10.0) # outer offset
        vsk.geometry(offset0)
        vsk.geometry(offset1)

    def finalize(self, vsk: vsketch.Vsketch) -> None:
        # We can automatically apply vpype settings here too!
        vsk.vpype("linemerge linesimplify reloop linesort")


if __name__ == "__main__":
    Sapeck03FParallelpolylineVskSketch.display()

G: Lines of Different Weights

#!/usr/bin/env python3
#
# sapeck_03_G_LinesOfDifferentWeights.py
# Draw different weight lines using offset curves
# Originally created by sapeck 2021-09-15
# CMU 60-428 F21 Drawing With Machines
#

from math import cos, sin

from shapely.geometry import LineString, MultiLineString
import vsketch

PI = 3.14159

class Sapeck03GLinesofdifferentweightsSketch(vsketch.SketchClass):
    CIRCLE_POINTS = 100
    RADIUS = 2
    OFFSET_AMOUNT = 0.0025
    OFFSET_NUM = 10

    def draw(self, vsk: vsketch.Vsketch) -> None:
        vsk.size("letter", landscape=False)
        vsk.scale("in")

        # This makes a teardrop-like shape
        points = [(0, 0)]
        for i in range(0, self.CIRCLE_POINTS):
          x = self.RADIUS * cos(i * (PI / self.CIRCLE_POINTS))
          y = self.RADIUS * sin(i * (PI / self.CIRCLE_POINTS)) + self.RADIUS + 1
          points.append((x, y))
        points.append((0, 0))
        
        # points is just an array of (x, y) points
        line = LineString(points)
        vsk.stroke(1)
        vsk.geometry(line)
        
        # Now make the inner offsets
        vsk.stroke(2)
        for i in range(0, self.OFFSET_NUM):
          offset = line.parallel_offset(i * self.OFFSET_AMOUNT, 'left',  join_style=2, mitre_limit=10.0) # inner offset
          vsk.geometry(offset)

    def finalize(self, vsk: vsketch.Vsketch) -> None:
        vsk.vpype("linemerge linesimplify reloop linesort")


if __name__ == "__main__":
    Sapeck03GLinesofdifferentweightsSketch.display()

H: Calligraphic Polyline

#!/usr/bin/env python3
#
# sapeck_03_H_CalligraphicPolyline.py
# Draw a calligraphic sine wave
# Originally created by sapeck 2021-09-15
# CMU 60-428 F21 Drawing With Machines
#

from math import cos, dist, sin

import numpy as np
from shapely.geometry import LineString, MultiLineString, Point
from shapely.ops import unary_union
import vsketch

PI = 3.14159

class Sapeck03HCalligraphicpolylineSketch(vsketch.SketchClass):
    CIRCLE_POINTS = 1000
    RADIUS = 3
    #OFFSET_AMOUNT = 0.0025
    OFFSET_AMOUNT = 0.0025
    OFFSET_MULTIPLIER = 600
    BLEED_OVER = 1

    def draw(self, vsk: vsketch.Vsketch) -> None:
        vsk.size("letter", landscape=True)
        vsk.scale("in")

        # This makes a teardrop-like shape
        points = []
        for i in range(0, self.CIRCLE_POINTS):
          x = i * (2 * PI / self.CIRCLE_POINTS)
          y = self.RADIUS * sin(x)
          points.append((x, y))
        
        last = None
        for point_i in range(0, len(points) - 1):
          prev_point = points[len(points) - 1] if point_i == 0 else points[point_i - 1]
          point = points[point_i]
          next_point = points[0] if point_i == len(points) - 1 else points[point_i + 1]
          change = dist(point, next_point)
          if change == 0:
            continue
          weight = 1 / (change * self.OFFSET_MULTIPLIER) # width of line
          num_lines = int(change / self.OFFSET_AMOUNT)
          orig = LineString([point, next_point])
          for i in range(1, num_lines + self.BLEED_OVER):
            next_point_shortened = orig.interpolate(i / num_lines, normalized=True)
            orig_short = LineString([Point(point[0], point[1]), next_point_shortened])
            # find perpendicular https://stackoverflow.com/a/57072678
            left = orig_short.parallel_offset(weight / 2, 'left')
            right = orig_short.parallel_offset(weight / 2, 'right')
            c = left.boundary[1]
            d = right.boundary[0]  # note the different orientation for right offset
            last = d
            vsk.geometry(LineString([c, d]))
          
          

    def finalize(self, vsk: vsketch.Vsketch) -> None:
        vsk.vpype("linemerge linesimplify reloop linesort")


if __name__ == "__main__":
    Sapeck03HCalligraphicpolylineSketch.display()

miniverse Line Excersizes

caligraphic polyline (SVG suitable)

https://editor.p5js.org/miniverse/sketches/TRGotFUpz

weighted line

https://editor.p5js.org/miniverse/sketches/oK1cOWPCu

offset line

https://editor.p5js.org/miniverse/sketches/06DRWU4wX

 

chaotic line

https://editor.p5js.org/miniverse/sketches/KaTwXMY-V

living line

https://editor.p5js.org/miniverse/sketches/PRvFEXkGr

dash line

https://editor.p5js.org/miniverse/sketches/S8XAu2l29

spiral

https://editor.p5js.org/miniverse/sketches/8b0d7tQ7C

 

 

lsh-LineExercises

I decided to do the following exercises in Rust as a technical challenge. This proved to be a little bit more of an undertaking than I expected, so here are some notes on some of the hurdles I ran into.

I decided to use nannou for most of the exercises, since I did not want to attempt implementing each interaction I needed in WGPU. Nannou seems incredibly powerful, but the guide left much to be desired (when they become more complete I will definitely come back for another look!). Figuring out registering the events I cared about took a significant amount of searching, since the guide did not seem to document it. Eventually I ended up using the all_functions example as a base and removing everything I didn’t care about. The second quirk that came up was nannou’s coordinate system, which puts the origin at the center of the screen. This proved to be problematic later on as I moved to SVG.

Rust also is completely opposed to implicit casts, which is fair, but also meant a lot of code was shifting between data structures. This was particularly apparent in managing the points for lines, which required taking the VecDeque.to_owned() each frame for drawing the polyline.

The SVG generation was its own ordeal. Nannou’s line builder seems to use the lyon package for SVG rendering. Lyon however does not allow actually exporting an SVG, so I ended up using the svg crate. It is also worth mentioning that the svg crate seems to be set up in a way which makes it hard to create SVGs programmatically. Specifically, I had to define the “Data” element mutable and constantly reassign it to the result of data.move_to() or data.line_to().

All in all, I would say the technical challenge was fun to play with, but I would not recommend this method over more mature frameworks like Processing or openFrameworks.

Feel free to check out the code behind the images above on GitHub.

grape – LineExercises

A.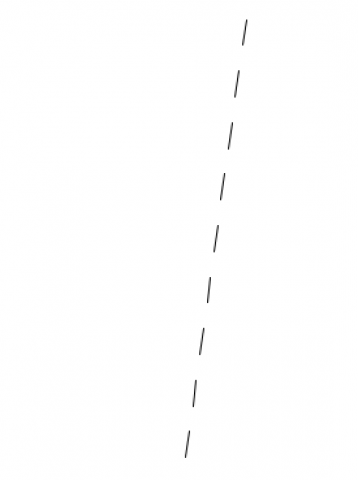 

/* Basically I used the example code from the lerp() page on Processing
 * but changed it so it would produce dotted lines for any random
 * pair of vectors
 * */
float dashed_length = 20;

void setup(){
  size(400, 400);
  background(100);
}

void draw(){
  background(255);
  int x1 = int(random(0,width));
  int x2 = int(random(0,width));
  int y1 = int(random(0,height));
  int y2 = int(random(0,height));
  
  float ydif = y2-y1;
  float xdif = x2-x1;
  float num_lines = sqrt(pow(ydif,2) + pow(xdif,2))/dashed_length;
  print(num_lines);
  
  for (int i = 0; i <= int(num_lines); i+=2) {
    float dx1 = lerp(x1, x2, i/num_lines) + num_lines;
    float dx2 = lerp(x1, x2, (i+1)/num_lines) + num_lines;
    float dy1 = lerp(y1, y2, i/num_lines);
    float dy2 = lerp(y1, y2, (i+1)/num_lines);
    line(dx1, dy1, dx2, dy2);
  }
  noLoop();
}

B.

C.

/**
 * I basically altered the brownian motion tutorial from Processing
 * to record mouseX, mouseY instead of random movement.
 */
 
int num = 100;
int range = 6;

float[] ax = new float[num];
float[] ay = new float[num]; 
float[] dx = new float[num];
float[] dy = new float[num];
// float[][] a = new float[num][2]; // LIVING LINE 2D ARRAY
// PVector[] a = new PVector[num]; // LIVING LINE PVECTORS
void setup() 
{
  size(640, 360);
  for(int i = 0; i < num; i++) {
    ax[i] = width/2;
    ay[i] = height/2;
    dx[i] = 0;
    dy[i] = 0;
  }
  /* LIVING LINE PVECTORS
  for(int i = 0; i < num; i++) {
    a[i] = new PVector();
    a[i].x = width/2;
    a[i].y = height/2;
  }
  */
  /* LIVING LINE 2D ARRAY
  for(int i = 0; i < num; i++){
    for(int j = 0; j < 2; j++){
      a[i][j] = width/2;
    }
  }
  */
  frameRate(30);
}

void draw() 
{
  background(255);
  
  // Shift all elements 1 place to the left
  for(int i = 1; i < num; i++) {
    dx[i-1] = dx[i];
    dy[i-1] = dy[i];
    ax[i-1] = ax[i];// + random(-range, range); SPICY LINE COMMENT
    ay[i-1] = ay[i];// + random(-range, range); SPICY LINE COMMENT
  }
  /* LIVING LINE PVECTORS
  for(int i = 1; i < num; i++) {
    a[i-1].x = a[i].x;
    a[i-1].y = a[i].y;
  }
  */
  /* // LIVING LINE 2D ARRAY
  for(int i = 1; i < num; i++){
    a[i-1][0] = a[i][0]; 
    a[i-1][1] = a[i][1];
  }
  */
  // Put a new value at the end of the array
  ax[num-1] = mouseX;
  ay[num-1] = mouseY;
  dx[num-1] = (ax[num-1] - ax[num-2]);
  dy[num-1] = (ay[num-1] - ay[num-2]);
  // a[num-1][0] = mouseX; // LIVING LINE 2D ARRAY
  // a[num-1][1] = mouseY; // LIVING LINE 2D ARRAY
  // a[num-1].x = mouseX; // LIVING LINE PVECTORS
  // a[num-1].y = mouseY; // LIVING LINE PVECTORS
  // Constrain all points to the screen
  //ax[num-1] = constrain(ax[num-1], 0, width);
  //ay[num-1] = constrain(ay[num-1], 0, height);
  
  // Draw a line connecting the points
  for(int i=1; i<num; i++) {    
    line(ax[i-1], ay[i-1], ax[i], ay[i]);
    // line(a[i-1].x, a[i-1].y, a[i].x, a[i].y); // LIVING LINE PVECTORS
    // line(a[i-1][0],a[i-1][1],a[i][0],a[i][1]); // LIVING LINE 2D ARRAY
  }
}

D.

E.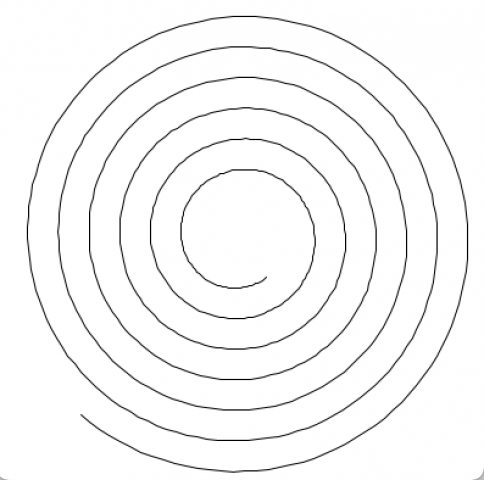 

float r = 40;


void setup(){
  size(400, 400);
  background(100);
}

void draw(){
  background(255);
  translate(width/2, height/2);
  //trig_circle();
  trig_spiral();
  noLoop();
}

void trig_spiral(){
  beginShape();
  for(float i = 1; i < 40; i+=0.05){
    vertex(cos(i)*(r), sin(i)*(r));
    r+=0.2;
  }
  endShape();
}

void trig_circle(){
  beginShape();
  for(float i = 1; i < 360; i+=1){
    vertex(cos(i)*(r), sin(i)*(r));
  }
  endShape();
}

F. I got tired of math so I made a shitty offset curve – not parallel, just the normal vector of the slope

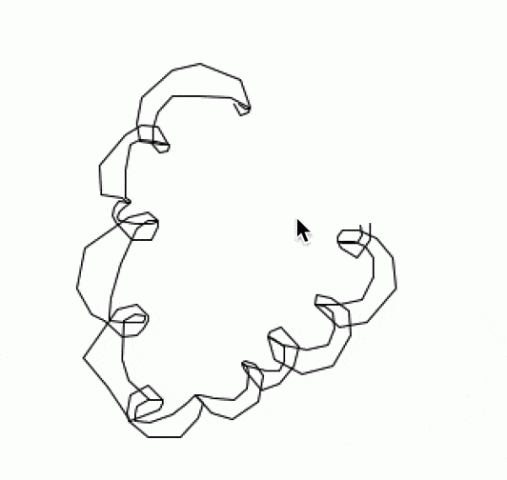
int num = 100;
int range = 6;

float[] ax = new float[num];
float[] ay = new float[num]; 
float[] dx = new float[num];
float[] dy = new float[num];
float[] ox = new float[num];
float[] oy = new float[num]; 
void setup() 
{
  size(640, 360);
  for(int i = 0; i < num; i++) {
    ax[i] = width/2;
    ay[i] = height/2;
    dx[i] = 0;
    dy[i] = 0;
    ox[i] = width/2;
    oy[i] = height/2;
  }
  frameRate(30);
}

void draw() 
{
  background(255);
  
  // Shift all elements 1 place to the left
  for(int i = 1; i < num; i++) {
    dx[i-1] = dx[i];
    dy[i-1] = dy[i];
    ax[i-1] = ax[i];
    ay[i-1] = ay[i];
    ox[i-1] = ox[i];
    oy[i-1] = oy[i];
  }
  // Put a new value at the end of the array
  ax[num-1] = mouseX;
  ay[num-1] = mouseY;
  dx[num-1] = (ax[num-1] - ax[num-2]);
  dy[num-1] = (ay[num-1] - ay[num-2]);
  //dksjfldkjslkdfjlsdj i hate this
  //ox[num-1] = 25/(1+pow((ay[num-1] + dx[num-1])/(ax[num-1] - dy[num-1]),2));
  //oy[num-1] = sqrt(25 - pow(ox[num-1],2));
  ox[num-1] = ax[num-1] - dy[num-1];
  oy[num-1] = ay[num-1] + dx[num-1];
  
  // Draw a line connecting the points
  for(int i=1; i<num; i++) {    
    //float val = float(i)/num * 204.0 + 51;
    //stroke(val);
    line(ax[i-1], ay[i-1], ax[i], ay[i]);
    //float dx = 25/(1+pow(ay[num-1] + dx[num-1]/ax[num-1] - dy[num-1]),2));
    //float dy = sqrt(25 - pow(dx,2));
    line(ox[i-1], oy[i-1], ox[i], oy[i]);
  }
}

G.

i was watching a lot of gordon ramsey

H.

“bears beets battlestar galactica”

import processing.svg.*;
int num = 1000;
int range = 6;

boolean record = false;

float[] ax = new float[num];
float[] ay = new float[num]; 
float[] dx = new float[num];
float[] dy = new float[num];
float[] ox = new float[num];
float[] oy = new float[num]; 

int num_lines = 5;
void setup() 
{
  size(640, 360);
  for(int i = 0; i < num; i++) {
    ax[i] = width/2;
    ay[i] = height/2;
    dx[i] = 0;
    dy[i] = 0;
    ox[i] = width/2;
    oy[i] = height/2;
  }
  frameRate(30);
}

void draw() 
{
  background(255);

  // Shift all elements 1 place to the left
  for(int i = 1; i < num; i++) {
    dx[i-1] = dx[i];
    dy[i-1] = dy[i];
    ax[i-1] = ax[i];
    ay[i-1] = ay[i];
    ox[i-1] = ox[i];
    oy[i-1] = oy[i];
  }
  // Put a new value at the end of the array
  ax[num-1] = mouseX;
  ay[num-1] = mouseY;
  dx[num-1] = (ax[num-1] - ax[num-2]);
  dy[num-1] = (ay[num-1] - ay[num-2]);
  
  // Draw a line connecting the points
  if(record){
    int now = millis();
    randomSeed(now);
    beginRecord(SVG, "foo_" + now + ".svg");
  }
  for(int i=1; i<num; i++) {    
    float mult = map(dx[i] + dy[i], 0, width+height, 1, 60);
    for(int j = 0; j < num_lines; j++){
      line(ax[i-1] - j*mult, ay[i-1], ax[i] - j*mult, ay[i]);
    }

  }
  if(record){
    endRecord();
    record = false;
  }
}

void keyPressed() {
  record = true;
}

BUT, then I added some perpendicular lines instead:

import processing.svg.*;
int num = 1500;
int range = 6;

boolean record = false;

float[] ax = new float[num];
float[] ay = new float[num]; 
float[] dx = new float[num];
float[] dy = new float[num];
float[] ox = new float[num];
float[] oy = new float[num]; 

int num_lines = 15;
void setup() 
{
  size(640, 640);
  for(int i = 0; i < num; i++) {
    ax[i] = width/2;
    ay[i] = height/2;
    dx[i] = 0;
    dy[i] = 0;
    ox[i] = width/2;
    oy[i] = height/2;
  }
  frameRate(30);
}

void draw() 
{
  background(255);

  // Shift all elements 1 place to the left
  for(int i = 1; i < num; i++) {
    dx[i-1] = dx[i];
    dy[i-1] = dy[i];
    ax[i-1] = ax[i];
    ay[i-1] = ay[i];
    ox[i-1] = ox[i];
    oy[i-1] = oy[i];
  }
  // Put a new value at the end of the array
  ax[num-1] = mouseX;
  ay[num-1] = mouseY;
  dx[num-1] = (ax[num-1] - ax[num-2]);
  dy[num-1] = (ay[num-1] - ay[num-2]);

  // Draw a line connecting the points
  if(record){
    int now = millis();
    randomSeed(now);
    beginRecord(SVG, "foo_" + now + ".svg");
  }
  for(int i=1; i<num; i++) {    
    float d_lines = int(map(dx[i] + dy[i],-200, 200, 0,num_lines));
    for(float j = 0; j < d_lines; j++){
      float multx1 = lerp(ax[i], ax[i-1], j/d_lines);
      float multx2 = lerp(ax[i]-dy[i], ax[i-1] - dy[i-1], j/d_lines);
      float multy1 = lerp(ay[i], ay[i-1], j/d_lines);
      float multy2 = lerp(ay[i] + dx[i], ay[i-1] + dx[i-1], j/d_lines);
      line(multx1, multy1, multx2, multy2);
    }
  }
  if(record){
    endRecord();
    record = false;
  }
}

void keyPressed() {
  record = true;
}

sweetcorn – LineExercises

int[] mouseCoordsX = new int[100];
int[] mouseCoordsY = new int[100];
PVector[] mouseCoords = new PVector[100];
PVector[] offsetCoords = new PVector[100];
int coordIndex = 0;
float growingNoise = 0;
boolean record;

import processing.svg.*;

void setup() {
  size(600, 600);
  stroke(255);
  strokeWeight(1);
  noFill();

  background(0);
}

void draw() {
}

void drawShakyLine() {
  growingNoise += 0.01;
  drawLivingLine(1, growingNoise);
}

void drawCircle(int mode) {
  float radius = (sqrt(pow(mouseX-(width/2), 2) + pow(mouseY - (height/2), 2)));

  if (mode == 0) {
    curveTightness(-0.7);
    beginShape();
    for (int i=0; i<2; i++) {
      curveVertex(radius + width/2, radius + height/2);
      curveVertex(radius + width/2, -radius + height/2);
      curveVertex(-radius + width/2, -radius + height/2);
      curveVertex(-radius + width/2, radius + height/2);
    }
    curveTightness(0);
    endShape();
  } else {
    push();
    translate(width/2 + 4*radius, height/2);
    float step = PI/12;
    for (float i=0; i<2*PI; i+=step) {
      rotate(step);
      translate(0, radius);
      line(0, 0, 0, -radius);
    }
    pop();
  }
}

void drawSpiral() {
  curveTightness(-0.7);
  beginShape();
  push();
  translate(width/2, height/2);
  float step = PI/12;
  for (float i=0; i<12*PI*mouseX/width; i+=step) {
    rotate(step);
    translate(0, i);
    line(0, 0, 0, -i);
  }
  pop();
}

void drawCalligraphicLine() {
  int lineSize = 10;

  beginShape();
  for (var i=lineSize; i<coordIndex-lineSize; i++) {

    float perpX = mouseCoords[i+lineSize].y - mouseCoords[i-lineSize].y;
    float perpY = mouseCoords[i-lineSize].x - mouseCoords[i+lineSize].x;

    float thickness = 200/sqrt(pow(perpX, 2) + pow(perpY, 2));

    float dist = sqrt(pow(perpX, 2) + pow(perpY, 2));

    perpX *= thickness/dist;
    perpY *= thickness/dist;

    offsetCoords[i] = new PVector(mouseCoords[i].x - perpX, mouseCoords[i].y - perpY);

    curveTightness(8);
    if (i%2 == 0) {
      curveVertex(offsetCoords[i].x, offsetCoords[i].y);
    } else {
      curveVertex(mouseCoords[i].x, mouseCoords[i].y);
    }
    curveTightness(0);
  }
  endShape();
}

void drawLineSeries() {
  push();
  translate(0, height/6);
  drawThickLine(1, width/6, 0, 5*width/6, 0);
  translate(0, height/6);
  drawThickLine(10, width/6, 0, 5*width/6, 0);
  translate(0, height/6);
  drawThickLine(20, width/6, 0, 5*width/6, 0);
  translate(0, height/6);
  drawThickLine(30, width/6, 0, 5*width/6, 0);
  translate(0, height/6);
  drawThickLine(40, width/6, 0, 5*width/6, 0);
  translate(0, height/6);
  drawThickLine(50, width/6, 0, 5*width/6, 0);
  pop();
}

void keyPressed() {
  if(key == 's') {
    record = true;
  }
}

void drawThickLine(int thickness, int x1, int y1, int x2, int y2) {
  int lineSize = 10;

  beginShape();
  for (var i=lineSize; i<coordIndex-lineSize; i++) {
    float perpX = mouseCoords[i+lineSize].y - mouseCoords[i-lineSize].y;
    float perpY = mouseCoords[i-lineSize].x - mouseCoords[i+lineSize].x;

    float dist = sqrt(pow(perpX, 2) + pow(perpY, 2));

    perpX *= thickness/dist;
    perpY *= thickness/dist;

    offsetCoords[i] = new PVector(mouseCoords[i].x - perpX, mouseCoords[i].y - perpY);

    curveTightness(8);
    if (i%2 == 0) {
      curveVertex(offsetCoords[i].x, offsetCoords[i].y);
    } else {
      curveVertex(mouseCoords[i].x, mouseCoords[i].y);
    }
    curveTightness(0);
  }
  endShape();
}

void mouseMoved() {
  background(0);
  
  if (record) {
    // Note that #### will be replaced with the frame number. Fancy!
    beginRecord(SVG, "frame-####.svg");
  }

  //drawDashedLine(); // 1
  //drawLivingLine(0, 0); // 2.1
  //drawLivingLine(1, 0); // 2.2
  //drawShakyLine(); // 3
  //drawCircle(0); // 4.1
  //drawCircle(1); // 4.2
  //drawSpiral(); // 5
  //drawLivingLine(2, 0); // 6
  //drawThickLine(0, 50); // 7.1
  //drawThickLine(1, 50); // 7.2
  //drawCalligraphicLine(); // 8
  drawLineSeries();

  if (coordIndex < 99) {
    coordIndex++;
  }

  mouseCoordsX[coordIndex] = mouseX;
  mouseCoordsY[coordIndex] = mouseY;

  mouseCoords[coordIndex] = new PVector(mouseX, mouseY);

  for (var i=0; i<coordIndex; i++) {
    mouseCoordsX[i] = mouseCoordsX[i+1];
    mouseCoordsY[i] = mouseCoordsY[i+1];

    mouseCoords[i] = mouseCoords[i+1];
  }
  
  if (record) {
    endRecord();
    record = false;
  }
}

void drawLivingLine(int mode, float noise) {
  beginShape();
  if (mode == 0) {
    for (var i=0; i < coordIndex; i++) {
      vertex(mouseCoordsX[i] + noise*randomGaussian(), mouseCoordsY[i] + noise*randomGaussian());
    }
  } else if (mode == 1) {
    for (var i=0; i < coordIndex; i++) {
      vertex(mouseCoords[i].x + noise*randomGaussian(), mouseCoords[i].y + noise*randomGaussian());
    }
  } else if (mode == 2) {
    for (var i=0; i < coordIndex; i++) {
      vertex(mouseCoords[i].x + noise*randomGaussian(), mouseCoords[i].y + noise*randomGaussian());
    }
    endShape();
    beginShape();
    int offset = 100;
    int lineSize = 10;
    for (var i=lineSize; i < coordIndex-lineSize; i++) {
      float perpX = mouseCoords[i+lineSize].y - mouseCoords[i-lineSize].y;
      float perpY = mouseCoords[i-lineSize].x - mouseCoords[i+lineSize].x;

      float dist = sqrt(pow(perpX, 2) + pow(perpY, 2));

      perpX *= offset/dist;
      perpY *= offset/dist;

      vertex(mouseCoords[i].x - perpX, mouseCoords[i].y - perpY);
    }
  }
  endShape();
}

void drawThickLine(int mode, int thickness) {
  int lineSize = 10;

  beginShape();
  for (var i=lineSize; i<coordIndex-lineSize; i++) {
    float perpX = mouseCoords[i+lineSize].y - mouseCoords[i-lineSize].y;
    float perpY = mouseCoords[i-lineSize].x - mouseCoords[i+lineSize].x;

    float dist = sqrt(pow(perpX, 2) + pow(perpY, 2));

    perpX *= thickness/dist;
    perpY *= thickness/dist;

    offsetCoords[i] = new PVector(mouseCoords[i].x - perpX, mouseCoords[i].y - perpY);

    if (mode == 0) {
      curveTightness(8);
      if (i%2 == 0) {
        curveVertex(offsetCoords[i].x, offsetCoords[i].y);
      } else {
        curveVertex(mouseCoords[i].x, mouseCoords[i].y);
      }
      curveTightness(0);
    } else if (mode == 1) {
      for (int j=0; j<thickness; j+=thickness/20) {
        if (j%thickness/40 == 0) {
          vertex(offsetCoords[i].x + j, offsetCoords[i].y);
        } else {
          vertex(mouseCoords[i].x, mouseCoords[i].y);
        }
      }
    }
  }
  endShape();
}

void drawDashedLine() {
  push();
  rotate(atan2(mouseY, mouseX));
  for (var i=0; i<sqrt(pow(mouseY, 2) + pow(mouseX, 2)); i+=20) {
    line(i, 0, i+10, 0);
  }
  pop();
}