Author: sweetcorn

sweetcorn-finalfinal

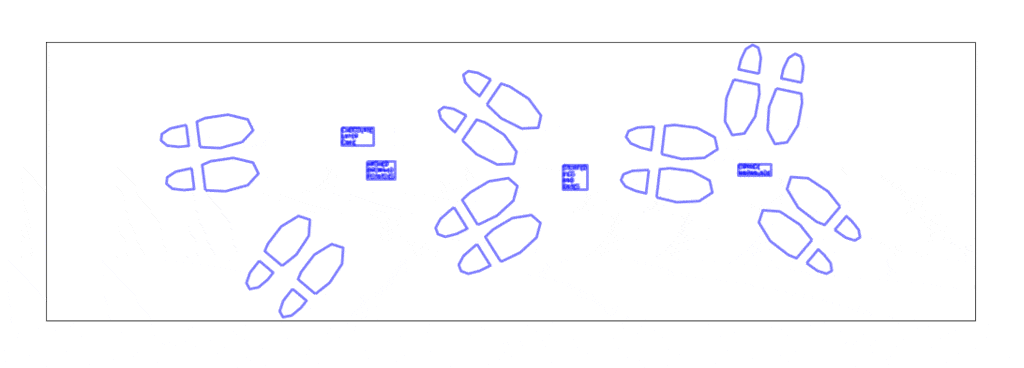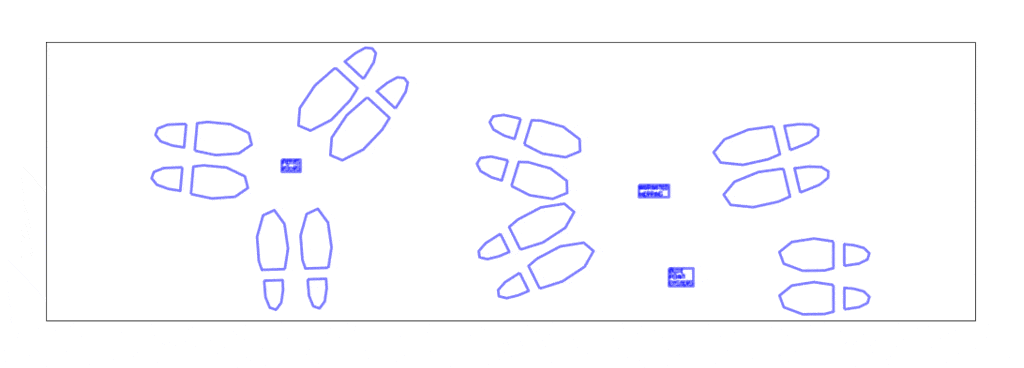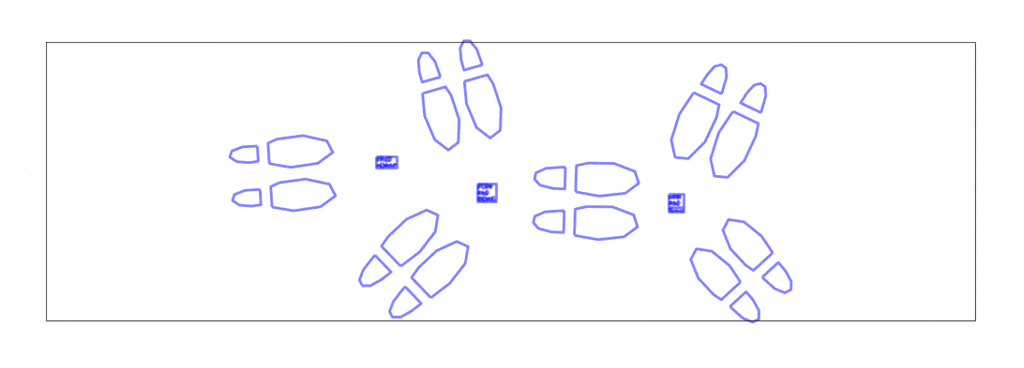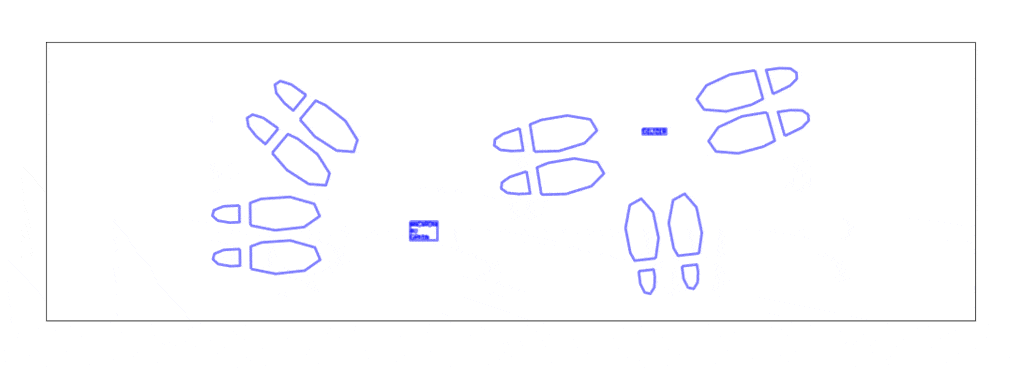
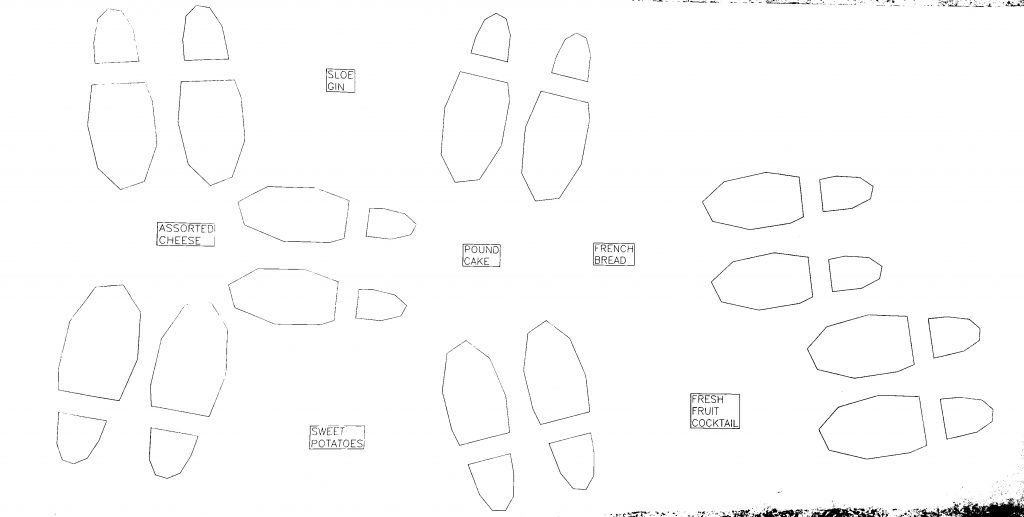
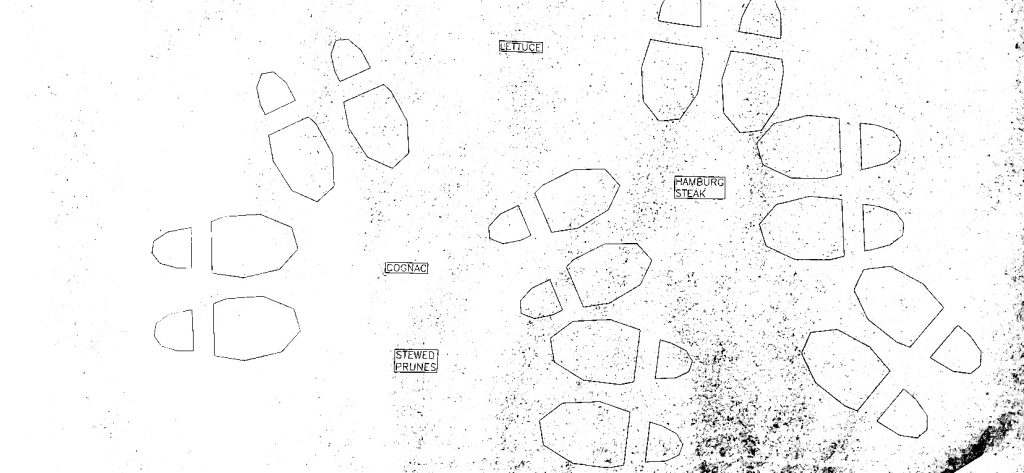
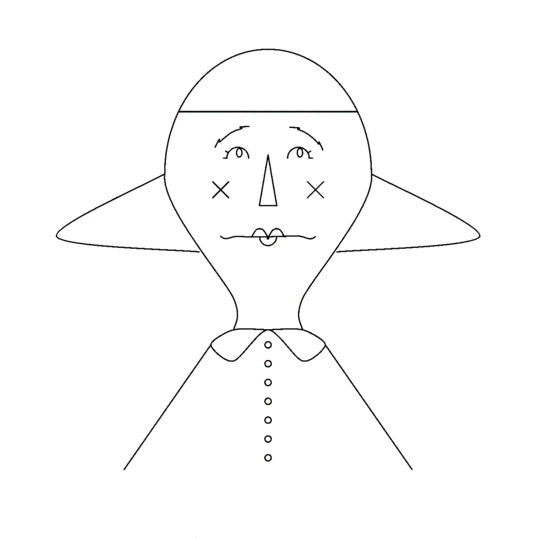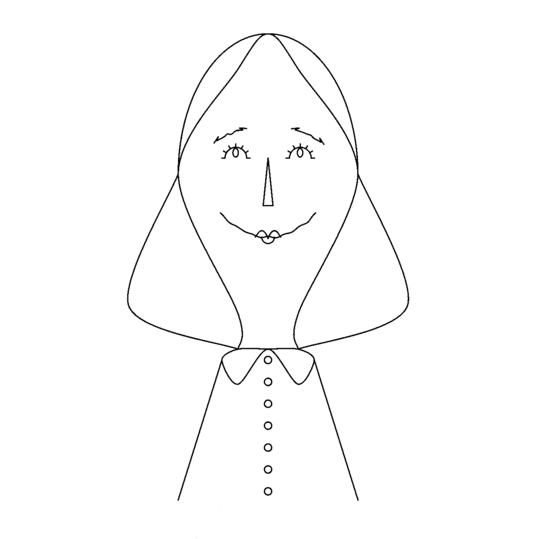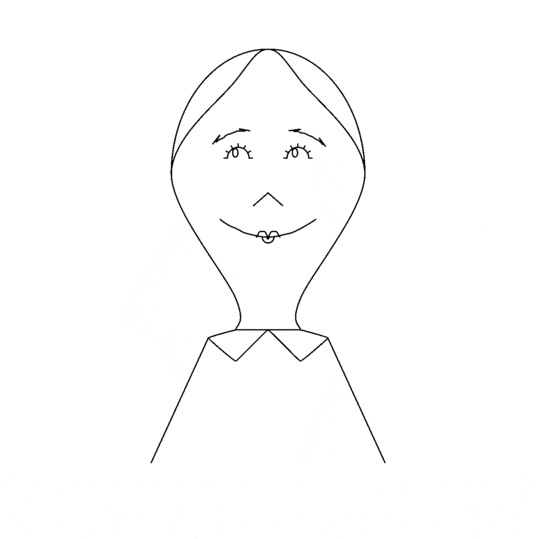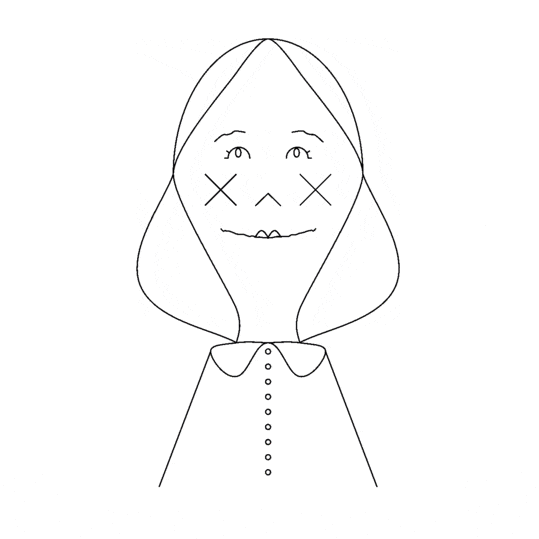
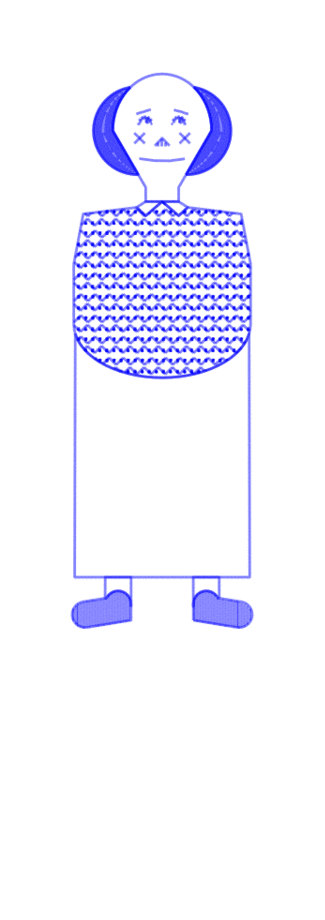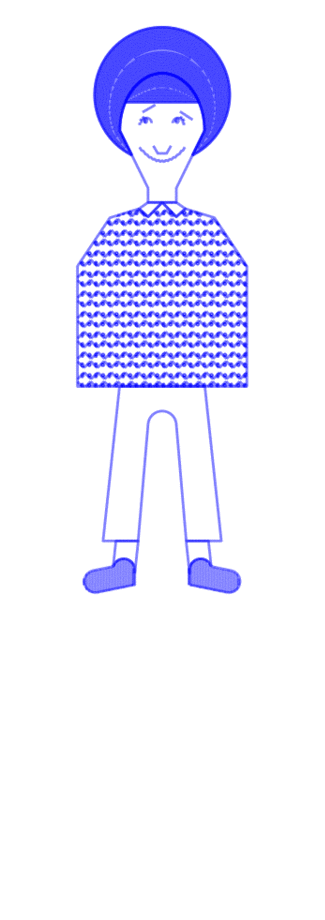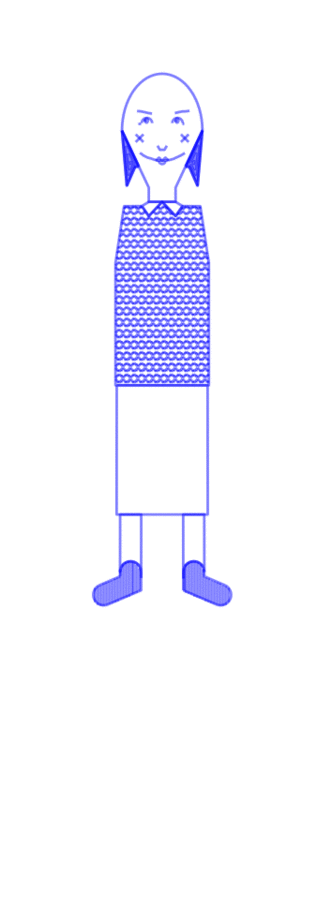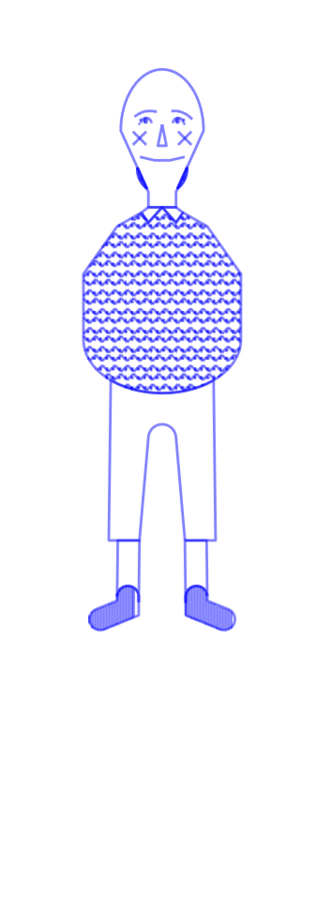
party-planning floor mat

17′ x 14’4″ floor installation containing 7 17′ x 30″ sheets of paper containing generated and plotted party text-objects and shoes connected by paths. 

Inspired by interactive floor-based works such as Clifford Owens’ Anthology (inspired by Warhol’s Dance Diagram) and George Snibbe’s Boundary Functions. Also inspired by Jenny Holzer’s work surrounding text, particularly her Truisms.

This work is situated in a larger body of my party-planning work, where party is a general term for community event (including birthday parties, funerals, family meals, mass, etc.).

Early experiments with abstract (non-textual) party objects at a smaller scale.

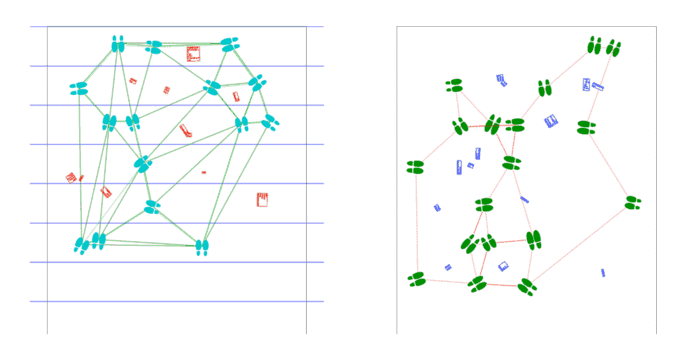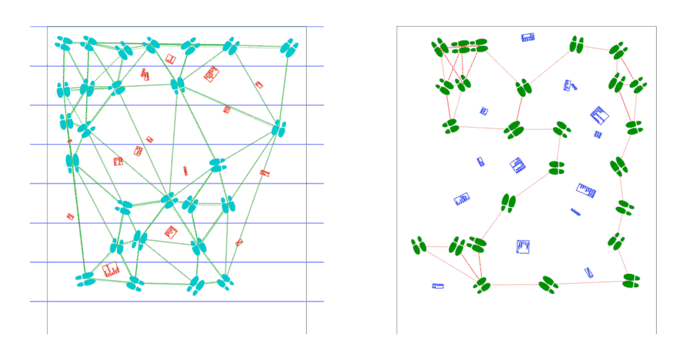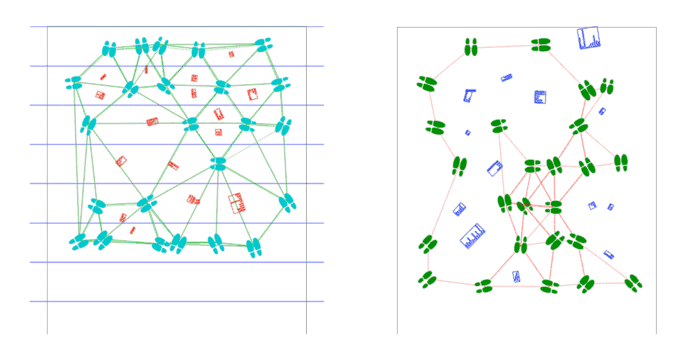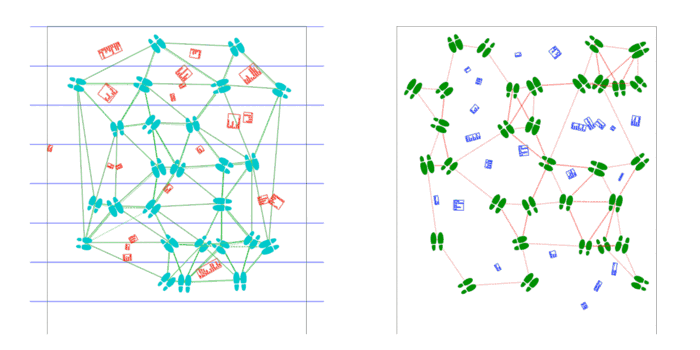
Shoes are placed by poisson-disc distribution and party objects are placed at voronoi vertices of these shoes. Shoes face the nearest party object and party objects face the average direction of the group of shoes facing them.

Later shift to text-based party objects at a larger scale.

Scaled-up program supports arbitrary length, as the USCutter supports any length fed by roll, as well as arbitrary width, as an arbitrary number of plots may be laid side-by-side. Installed on the first floor of CFA in a high traffic area.

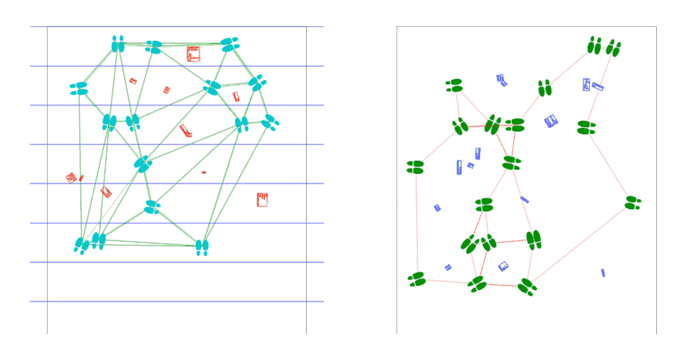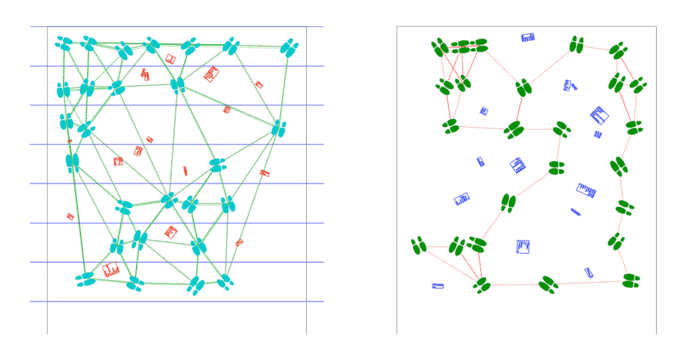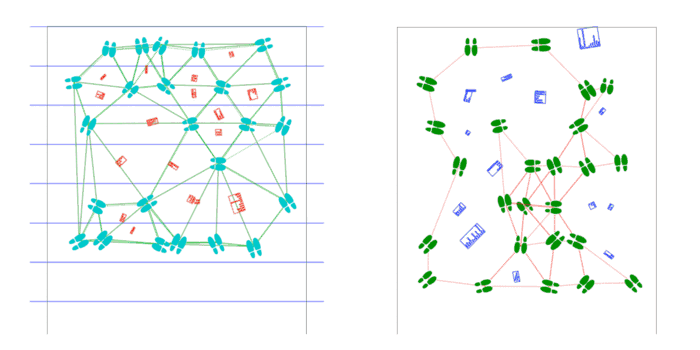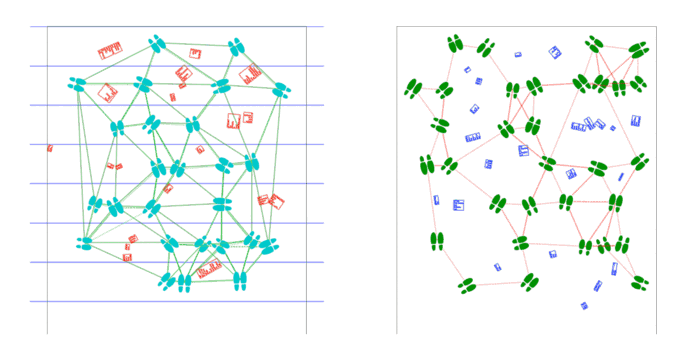
Text is pulled from a previous project of mine: Objects of Desire, a list of 18,336 things that are in some way desired, as determined by natural-language-processing techniques on all of Project Gutenberg.

 

 

fast-moving object capture

Experimentation with an open-cv-based algorithm for fast-moving-object detection loosely based on this paper. Boxes placed around detected fast-moving objects.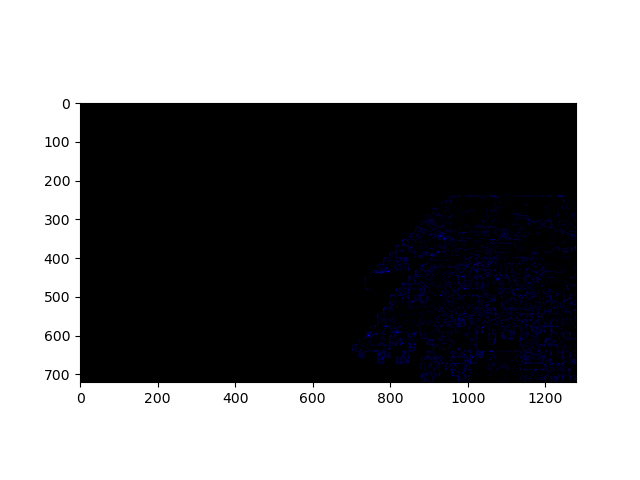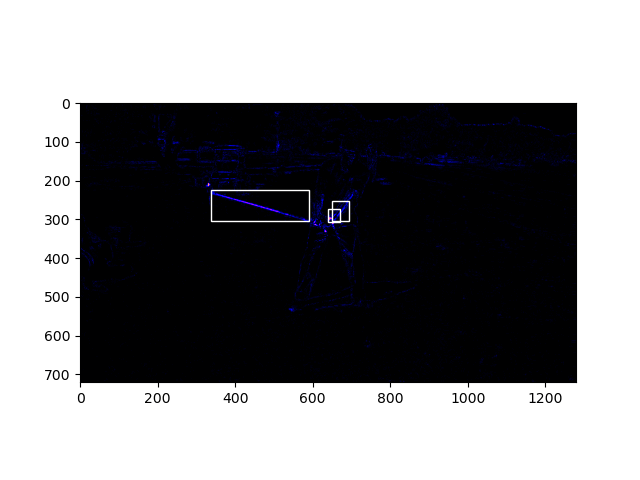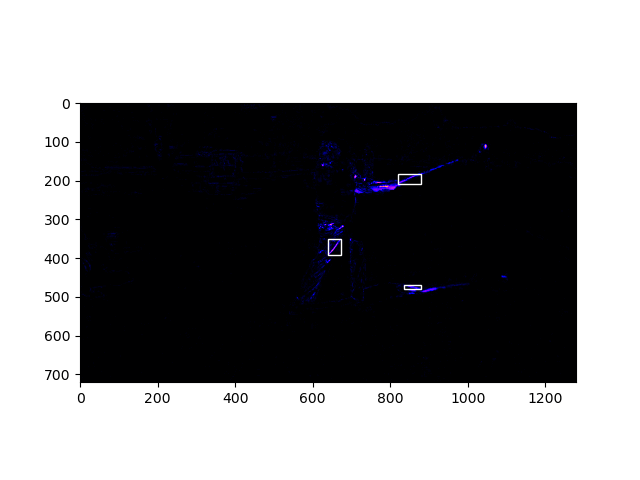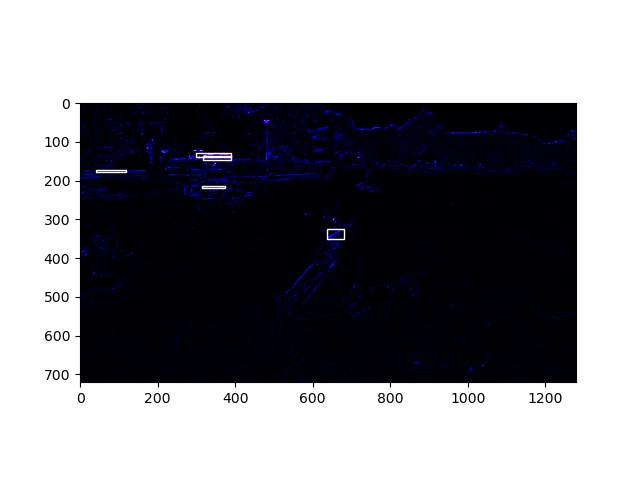Using this algorithm, I wrote a program which sorts a given video’s frames by the speed of the objects in each. The fastest-moving frames come first. I suppose we get the most excitement in the smallest amount of time this way. The number above each frame is the calculated speed of objects in it.

carl bowser

I plotted the found fastest frame of a clip of Carl Bowser (Turner’s sponsee) racing.

Here, I randomly chose a number of points and (incorrectly) assigned one of six pens (RGBCMY) on the HP7475A.

I resolved most of these color issues in my second attempt. Since marks made are larger than the image’s pixel size, the order of pens matters more than I had expected.

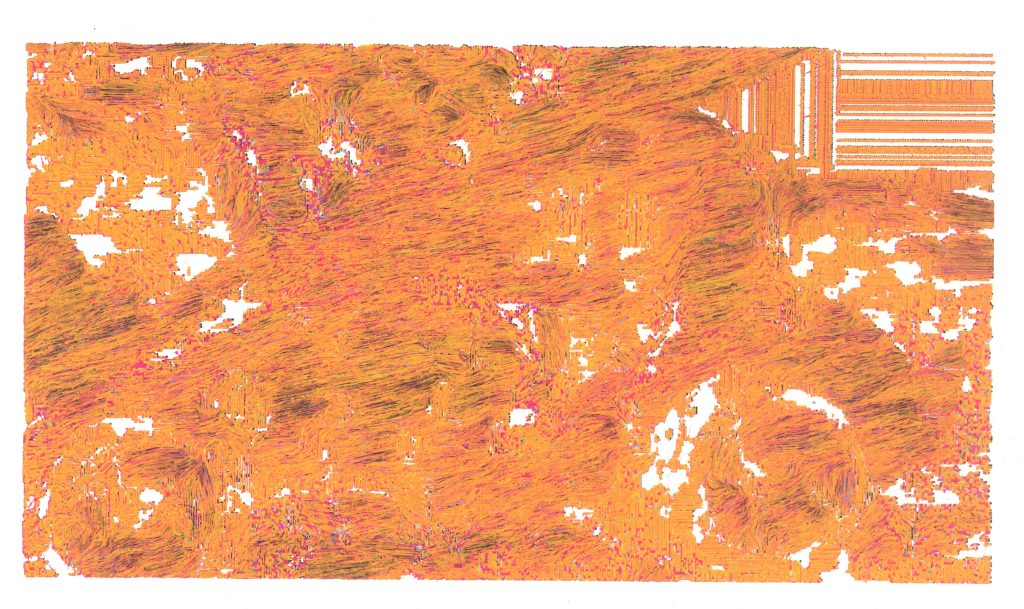
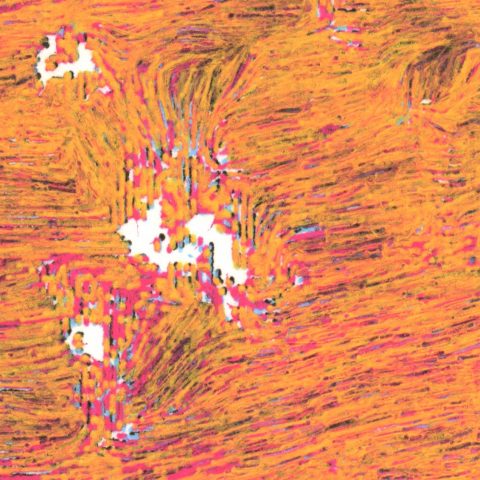
Instead of stippling the motion-blurred images, I decided to further utilize the material conditions allowed by the plotter by removing the areas containing blurs from the images, as shown below. The value of each pixel corresponds to the number of times the pen passes over it. The blank areas were then manually blurred by carefully brushing with water.

Further in this direction, I experimented with using line detection in the motion-blurred areas to render streaks as lines in the direction of the motion.

I changed directions completely when Golan showed me optical flow, which tracks the motion of points from one frame to the next. I used this, along with CMYK color mapping on the flow lines’ average underlying colors to plot the following test swatches and frame.

 

sweetcorn-finalproject

Party-Planning Floor Mat

I’m interested in creating objects which plan parties. (‘Party’ is used as a catch-all term for some community-expressive event).

The ideal party-planning object to me is (1) unique (i.e., no two instances of it are identical), (2) low-effort to set up, (3) widely usable, and (4) interactive (both in terms of interacting with the object and each party-goer interacting with the other party-goers).

As best I could, I created party-planning floor mats under these constraints. In terms of (1) uniqueness, each floor mat is entirely generated. The size is arbitrary, able to scale from the area of one pair of shoes to the surface area of the globe, given appropriate material. Each area is filled with shoes according to a poisson-disc distribution. Each shoe is parametric, with variables relating to height, width, and concavity (magnitude and location). Party objects are placed on appropriate vertices of the shoes’ voronoi diagram. Each party object is a random choice from a natural-language-processing-generated list of 18,336 things that are wanted or desired in some way. Shoes face the nearest party object and party objects face the general direction of all shoes facing them. A closed path from shoe to shoe is determined from a decent enough traveling-salesman solution. Below is a gif of the debug-mode, which shows the cuts and the voronoi diagram, next to the full generated floor mat.

These elements are divided into 25-inch-wide strips of arbitrary length, which can be plotted on a large enough plotter, such as the studio’s MH871. Each color must be plotted as a separate layer, which, in combination with the difficulty aligning the paper over such a long length, does not exactly meet (2) the criterion of low-effort. I likely spent upwards of 3 hours simply plotting this 7-sheet-wide, 17-foot-long floor mat. Machines capable of plotting on this scale are also not commonplace, meaning these party-planning files, at least, are not (3) widely usable. The sheets themselves, though, may meet these two criteria. A better method of securing the sheets to the floor and to each other would greatly simplify things. I wonder about the product-ness of these mats and party-planning objects in general.

Part of me wants to either abstract or remove the words altogether. I’m just not sure how well they work in terms of augmenting the interactions between party-goers. I’m also not sure about their influence on the mood of the piece; they likely read as more foreboding or poetic than a “party object.” Of course, parties as I’ve defined them don’t need to be cheerful, but Iworry it makes the work read more as “art object” than “party-planning object.”

(4) I did see many people afraid to step on it. Given permission, however, people seemed to be having fun with the mat and one another. Some of the paths are quite long and a good number of people nearly fell trying to jump from shoe to shoe. People also ended up standing much closer to one another than they might normally. Maybe they needed an excuse?

– xoxo
sweetcorn

sweetcorn – MidSemester

What good is a party without attendees?

For my mid-semester project, I chose to revise my generative people. I had lost a lot of charm when I ported my face generation code from JavaScript to python implementing vsketch with shapely, particularly due to the loss of curves that I had originally written with p5.js’s beginShape(), endShape(), and curveVertex(). I could have figured out the Bezier curves, but I don’t really care to do that. I rewrote the head and its associated coordinate system using a parametric cranioid equation that Golan sent me. I was not very smart in how I had set up a lot of placements last time. Instead of prescribing positions, this time I more often got the boundaries of previous geometries and used their positions to relatively place other geometries.

I also found my previous sweaters’ pattern to be a missed opportunity for variation. I implemented trimesh’s medial_axis functionality on the sweater (after adding arms and hands, which were unfortunate things to have left off last time) in order to get a simple structure off which I could base a faux-dimensionality. I broke the sweater into polygons using this medial axis and filled each polygon with the sweater’s original hershey-symbol-character-based pattern, this time sheared proportionally to the polygon’s centroid’s distance to the nearest point on the axis. This breaks the sweater into sections, each with a not very accurate three-dimensionality. Below is an image of the boundaries of each section that composes the sweater. I’m reminded of my Grandma on my Mom’s side, who would make and sell little flat paper-clothed dolls.

Below is a gif of several .svgs created, showing some of the range of the generativity. Note that the angle of the arms sometimes pushes them past the bounds of the paper (which in the here-horizontal direction is strict for the plotter) which is an error I have yet to fix. Often if the arms are generated in the down position, they form an internal polygon between the elbow and the body. That’s only natural, but trimesh and shapely are not handling that internal polygon very well for various reasons. The result is that most of the successfully-generated people have their arms in the air, which contributes to a certain anxiety to these figures which Mali pointed out.

These .svgs are converted into HPGL files using a custom config file for vpype to be plotted life-sized on the USCutter MH871-MK2. Below is a photo of a completed plot. For my last two projects, I had made the mistake of using too thin a drawing instrument for such large paper, leading to some legibility issues. This time, I used a thick purple sharpie and set the USCutter up such that significant pressure was applied to the paper with the sharpie, making a thicker line. I do wonder if the child-like quality of thick Crayola markers would be appropriate to use as I had for the first plot. Longevity isn’t exactly a concern, given the relatively short length of parties these figures are to attend. Most of the plotter-communication error I ran into last time must have been somehow due to the concentric filling of the hair, which I have since changed to simple vertical hatching. I also filled the pupils and sometimes the lips to the point where they appear solid. I fortunately ran into no plotting problems other than my laptop falling asleep before I plugged it in, stopping the transmission of data to the plotter. This put a big line right through my first plot. Not the first time I’ve made this mistake.

And for fun, a video of the sweater being plotted:

Future directions for this project include better sorting out the sweater-sectioning and shearing method to completely fill the sweaters dimensionally, adding more detail to the pants and shoes, implementing flow-field-based hair filling, multi-color plotting, and variance in pose/activity for each person. The goal in the end is to be able to generate and plot enough figures to have a lovely party.

~xoxo

sweetcorn – FieldComposition

Party Planning Floor-mat

I’m a fan of parties in an abstract sense of the word party: any sort of community event. For this project, I was inspired by Nick’s kissing tiles in the sense of treating the objects of these algorithms personally and personifying the interactions between them. Distributions of people across a space shouts nothing other than a lovely party.

At each point whose location was determined by poisson disc sampling (an implementation stolen from here), I placed a pair of shoes. Their curves are a vertically-stretched version of a parametric cranioid curve that Golan sent me to use for my generative people’s heads. A rectangular slice is taken out near the convexity to look more like a shoe-print. Given this set of points, I obtained a voronoi diagram with SciPy and placed a special party object at each node that fell within the party space, but not too close to any other party object. I oriented each pair of shoes to face their nearest party object. These party objects could be any sort of thing: televisions, tables, chairs, but many if not most parties are centered around food, so I placed a marker for unique food at each party object location. The names of these foods were taken from dariusk’s corpora project, which has a list of “the top 1000 most appearing menu items from the 1850s to today from the New York Public Library’s ‘What’s on the menu?’ project.” I rendered a random choice from this list in the Hershey font library I’ve been using.

Here are a few generated .svg’s:

and a couple plotted on the USCutter MH871-MK2 (the feet are full-size, the paper is ~30 in. x 75 in.):

sweetcorn-TilingPattern

For my project, I picked up an old project of mine which generated childrens’-story-esque faces. I worked on this before becoming familiar with Shapely, so I had hadn’t implemented any sort of filling. I brought this old code from JavaScript to python and converted everything into Shapely geometries. Below is some documentation from the old project.

With my work last week figuring out how to plot on the USCutter MH871-MK2, I figured it would be lovely to generate and plot human-sized figures.

The hair and shoes are filled with simple hatching, but the shirt has a pattern build out of Hershey fonts. Using this python hershey font library, I randomly choose symbol characters and place them between arrangements of {}, /\, or two opposite-facing integral symbols. I use shapely to crop all the fills to their respective polygons. Below is a gif containing a few generated .svg’s

A video of the plot in progress:

And some plotted results:

 

 

sweetcorn – DrawingBots

In the discord, someone linked this article about “decorative knotting using Trigonometric Parametrizations.” In it are many equations for creating decorative knots, which I think would fit well in terms of my exploration of flourishes. These equations are for three dimensions, which makes sense because knots have to be three-dimensional, so if I were to implement any of these, I could somehow project this into 2D, which the discord has resources on and links this repo, which could be useful.

sweetcorn – LineExercises

int[] mouseCoordsX = new int[100];
int[] mouseCoordsY = new int[100];
PVector[] mouseCoords = new PVector[100];
PVector[] offsetCoords = new PVector[100];
int coordIndex = 0;
float growingNoise = 0;
boolean record;

import processing.svg.*;

void setup() {
  size(600, 600);
  stroke(255);
  strokeWeight(1);
  noFill();

  background(0);
}

void draw() {
}

void drawShakyLine() {
  growingNoise += 0.01;
  drawLivingLine(1, growingNoise);
}

void drawCircle(int mode) {
  float radius = (sqrt(pow(mouseX-(width/2), 2) + pow(mouseY - (height/2), 2)));

  if (mode == 0) {
    curveTightness(-0.7);
    beginShape();
    for (int i=0; i<2; i++) {
      curveVertex(radius + width/2, radius + height/2);
      curveVertex(radius + width/2, -radius + height/2);
      curveVertex(-radius + width/2, -radius + height/2);
      curveVertex(-radius + width/2, radius + height/2);
    }
    curveTightness(0);
    endShape();
  } else {
    push();
    translate(width/2 + 4*radius, height/2);
    float step = PI/12;
    for (float i=0; i<2*PI; i+=step) {
      rotate(step);
      translate(0, radius);
      line(0, 0, 0, -radius);
    }
    pop();
  }
}

void drawSpiral() {
  curveTightness(-0.7);
  beginShape();
  push();
  translate(width/2, height/2);
  float step = PI/12;
  for (float i=0; i<12*PI*mouseX/width; i+=step) {
    rotate(step);
    translate(0, i);
    line(0, 0, 0, -i);
  }
  pop();
}

void drawCalligraphicLine() {
  int lineSize = 10;

  beginShape();
  for (var i=lineSize; i<coordIndex-lineSize; i++) {

    float perpX = mouseCoords[i+lineSize].y - mouseCoords[i-lineSize].y;
    float perpY = mouseCoords[i-lineSize].x - mouseCoords[i+lineSize].x;

    float thickness = 200/sqrt(pow(perpX, 2) + pow(perpY, 2));

    float dist = sqrt(pow(perpX, 2) + pow(perpY, 2));

    perpX *= thickness/dist;
    perpY *= thickness/dist;

    offsetCoords[i] = new PVector(mouseCoords[i].x - perpX, mouseCoords[i].y - perpY);

    curveTightness(8);
    if (i%2 == 0) {
      curveVertex(offsetCoords[i].x, offsetCoords[i].y);
    } else {
      curveVertex(mouseCoords[i].x, mouseCoords[i].y);
    }
    curveTightness(0);
  }
  endShape();
}

void drawLineSeries() {
  push();
  translate(0, height/6);
  drawThickLine(1, width/6, 0, 5*width/6, 0);
  translate(0, height/6);
  drawThickLine(10, width/6, 0, 5*width/6, 0);
  translate(0, height/6);
  drawThickLine(20, width/6, 0, 5*width/6, 0);
  translate(0, height/6);
  drawThickLine(30, width/6, 0, 5*width/6, 0);
  translate(0, height/6);
  drawThickLine(40, width/6, 0, 5*width/6, 0);
  translate(0, height/6);
  drawThickLine(50, width/6, 0, 5*width/6, 0);
  pop();
}

void keyPressed() {
  if(key == 's') {
    record = true;
  }
}

void drawThickLine(int thickness, int x1, int y1, int x2, int y2) {
  int lineSize = 10;

  beginShape();
  for (var i=lineSize; i<coordIndex-lineSize; i++) {
    float perpX = mouseCoords[i+lineSize].y - mouseCoords[i-lineSize].y;
    float perpY = mouseCoords[i-lineSize].x - mouseCoords[i+lineSize].x;

    float dist = sqrt(pow(perpX, 2) + pow(perpY, 2));

    perpX *= thickness/dist;
    perpY *= thickness/dist;

    offsetCoords[i] = new PVector(mouseCoords[i].x - perpX, mouseCoords[i].y - perpY);

    curveTightness(8);
    if (i%2 == 0) {
      curveVertex(offsetCoords[i].x, offsetCoords[i].y);
    } else {
      curveVertex(mouseCoords[i].x, mouseCoords[i].y);
    }
    curveTightness(0);
  }
  endShape();
}

void mouseMoved() {
  background(0);
  
  if (record) {
    // Note that #### will be replaced with the frame number. Fancy!
    beginRecord(SVG, "frame-####.svg");
  }

  //drawDashedLine(); // 1
  //drawLivingLine(0, 0); // 2.1
  //drawLivingLine(1, 0); // 2.2
  //drawShakyLine(); // 3
  //drawCircle(0); // 4.1
  //drawCircle(1); // 4.2
  //drawSpiral(); // 5
  //drawLivingLine(2, 0); // 6
  //drawThickLine(0, 50); // 7.1
  //drawThickLine(1, 50); // 7.2
  //drawCalligraphicLine(); // 8
  drawLineSeries();

  if (coordIndex < 99) {
    coordIndex++;
  }

  mouseCoordsX[coordIndex] = mouseX;
  mouseCoordsY[coordIndex] = mouseY;

  mouseCoords[coordIndex] = new PVector(mouseX, mouseY);

  for (var i=0; i<coordIndex; i++) {
    mouseCoordsX[i] = mouseCoordsX[i+1];
    mouseCoordsY[i] = mouseCoordsY[i+1];

    mouseCoords[i] = mouseCoords[i+1];
  }
  
  if (record) {
    endRecord();
    record = false;
  }
}

void drawLivingLine(int mode, float noise) {
  beginShape();
  if (mode == 0) {
    for (var i=0; i < coordIndex; i++) {
      vertex(mouseCoordsX[i] + noise*randomGaussian(), mouseCoordsY[i] + noise*randomGaussian());
    }
  } else if (mode == 1) {
    for (var i=0; i < coordIndex; i++) {
      vertex(mouseCoords[i].x + noise*randomGaussian(), mouseCoords[i].y + noise*randomGaussian());
    }
  } else if (mode == 2) {
    for (var i=0; i < coordIndex; i++) {
      vertex(mouseCoords[i].x + noise*randomGaussian(), mouseCoords[i].y + noise*randomGaussian());
    }
    endShape();
    beginShape();
    int offset = 100;
    int lineSize = 10;
    for (var i=lineSize; i < coordIndex-lineSize; i++) {
      float perpX = mouseCoords[i+lineSize].y - mouseCoords[i-lineSize].y;
      float perpY = mouseCoords[i-lineSize].x - mouseCoords[i+lineSize].x;

      float dist = sqrt(pow(perpX, 2) + pow(perpY, 2));

      perpX *= offset/dist;
      perpY *= offset/dist;

      vertex(mouseCoords[i].x - perpX, mouseCoords[i].y - perpY);
    }
  }
  endShape();
}

void drawThickLine(int mode, int thickness) {
  int lineSize = 10;

  beginShape();
  for (var i=lineSize; i<coordIndex-lineSize; i++) {
    float perpX = mouseCoords[i+lineSize].y - mouseCoords[i-lineSize].y;
    float perpY = mouseCoords[i-lineSize].x - mouseCoords[i+lineSize].x;

    float dist = sqrt(pow(perpX, 2) + pow(perpY, 2));

    perpX *= thickness/dist;
    perpY *= thickness/dist;

    offsetCoords[i] = new PVector(mouseCoords[i].x - perpX, mouseCoords[i].y - perpY);

    if (mode == 0) {
      curveTightness(8);
      if (i%2 == 0) {
        curveVertex(offsetCoords[i].x, offsetCoords[i].y);
      } else {
        curveVertex(mouseCoords[i].x, mouseCoords[i].y);
      }
      curveTightness(0);
    } else if (mode == 1) {
      for (int j=0; j<thickness; j+=thickness/20) {
        if (j%thickness/40 == 0) {
          vertex(offsetCoords[i].x + j, offsetCoords[i].y);
        } else {
          vertex(mouseCoords[i].x, mouseCoords[i].y);
        }
      }
    }
  }
  endShape();
}

void drawDashedLine() {
  push();
  rotate(atan2(mouseY, mouseX));
  for (var i=0; i<sqrt(pow(mouseY, 2) + pow(mouseX, 2)); i+=20) {
    line(i, 0, i+10, 0);
  }
  pop();
}

sweetcorn – LostrittoReading

Something that stuck out to me in the Lostritto reading was the section about mark-making and editing. I remember Natalie Westbrook telling us in Drawing I that the eraser was a drawing tool itself. It made sense in that context since we would cover paper in charcoal and draw with the eraser. Lostritto’s declaration of more or less the same thing clicked differently for me. If I draw one thing, erase it, and draw  a second thing on top, that produces an entirely different thing than just drawing the second thing. It makes me think about the aesthetics of errors, which is a popular thing in the computational or internet or digital world with the glitch aesthetic. I think about the possibilities of attaching an eraser to a plotter after attaching a pencil and having a longer-term piece and the dialogue between that pencil and that eraser.