I created a boba clock which is milk tea with boba from noon to midnight and juice with lychee jelly from midnight to noon. The number of Jelly/Boba inside the cup, including one inside the straw, represents the hour. Juice/milk shrinks per second, and the full amount disappears per minute. Lastly, a Jelly/Boba stuck inside the straw moves upward per minute and got out from the straw each hour.
sketchDownload//Alicia Kim
//Section B
var x = [];
var y = [];
var angle = [];
function setup() {
createCanvas(300, 400);
for (var i=0; i<(hour()%12-1); i+=1) {
x[i] = random (120,190);
y[i] = random (200,340);
angle[i] = random(360);
}
for(var j=0; j<height; j+=1){
stroke(lerpColor(color(255,232,239) ,color(255,253,208),j/height));
line(0,j,width,j);
}
}
function draw() {
var s = second();
var min = minute();
stroke(0);
//juice with lychee jelly from midnight to noon
//& milk tea with boba from noon to midniht
push();
if (hour()>12){
drawMilk(s);
}
else if (hour()<=12){
drawJuice(s);
}
pop();
push ();
drawCup();
pop();
push();
drawStraw();
pop();
push();
if (hour()>12){
drawBoba();
strawBoba(min);
}
else if (hour()<=12){
drawJelly();
strawJelly(min);
}
pop();
}
// juice inside the cup shrinks per sec
function drawJuice(s){
fill(255,203,164); //orange
quad(70,75,230,75,215,350,85,350); //juice
//cover
fill(255);
quad(70,75,230,75,230-(15/60)*s,75+s*(275/60),70+(15/60)*s,75+s*(275/60));
stroke(255,178,120); //dark orange
fill(255,203,164);
ellipse (width/2, 75+(275/60)*s, 160-(0.5)*s, 60);
}
function drawCup(){
// bigger circle
fill(224,255,255); //light cyan
ellipse (width/2, 75 , 160, 60);
// smaller circle
push();
if (hour()<=12){
fill(255,203,164);
}
else if (hour()>12){
fill(247,231,200);
}
ellipse (width/2, 350, 130, 50);
pop();
//connecting lines
line (70, 75, 85, 350);
line (230, 75, 215, 350);
}
function drawStraw(){
// straw body
push();
fill(0,191,255,50); //sky blue
rect(140,30,20,300);
pop();
// straw holes
ellipse(width/2,30,20,10);
ellipse(width/2,330,20,10);
fill(224,255,255); //light cyan
arc (width/2, 75 , 160, 60, 0, PI, OPEN);
}
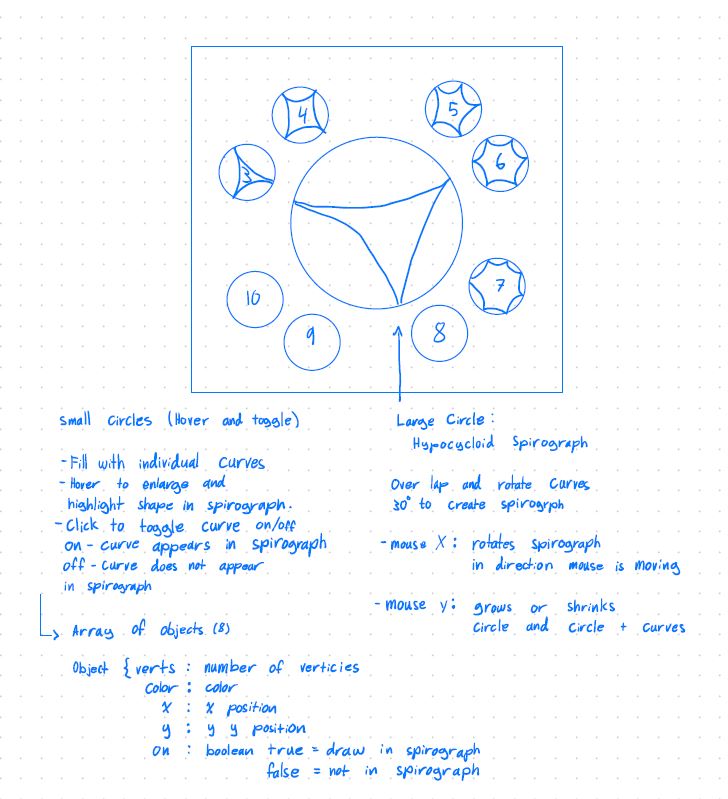
// number of jelly inside the cup represents the hour
function drawJelly(){
for (var i=0; i<(hour()%12-1); i++) {
push();
translate(x[i],y[i]);
rotate(radians(angle[i]));
noStroke();
fill(249,246,231,150); //lychee
rect (0,0,10,30); //lychee jelly
pop();
}
}
// jelly inside the straw moves up per minute
function strawJelly(m){
noStroke();
fill(255,255,142);
rect (width/2-5,300-(225/60)*m,10,30);
}
// milk inside the cup shrinks per sec
function drawMilk(s){
stroke(236,220,194); //dark milk color
fill(247,231,200); //milk color
quad(70,75,230,75,215,350,85,350); //juice
//cover
fill(255);
quad(70,75,230,75,230-(15/60)*s,75+s*(275/60),70+(15/60)*s,75+s*(275/60));
fill(247,231,200); //milk color
ellipse (width/2, 75+(275/60)*s, 160-(0.5)*s, 60);
}
// number of boba inside the cup & straw represents the hour
function drawBoba(){
for (var i=0; i<(hour()%12-1); i++) {
push();
stroke(70, 51, 51,100); //darker brown
fill(88,59,57,150); //dark brown
ellipse (x[i],y[i],20,20); //boba
pop();
}
}
// boba inside the straw moves up per minute
function strawBoba(m){
noStroke();
fill(88,59,57);
ellipse (width/2,300-(225/60)*m,20,20);
}
![[OLD SEMESTER] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2023/09/stop-banner.png)