Observations:
- The artwork seems to consist of a mixture of square and rectangular cells, but at closer inspection it is composed of square cells with subdivisions.
- Each square cell has one or two rectangular subdivisions that are hatched with lines.
- The subdivisions are chosen out of a pool of 4 – top, bottom, left, or right. There is no restriction on which subdivisions can be paired with each other – some have top and bottom, right and bottom, top and left, etc.
- Most cells have two subdivisions, only a select few have one.
- Sometimes a subdivision has two different patterns in it.
- The patterns use the same pen weight throughout the print.
- On rare occasions the subdivision rule is broken for the following pattern:

- The aforementioned pattern breaks the subdivision and cells rule. It bleeds into neighboring cells.
- Occasionally, a cell will generate a diagonal line that starts at a corner and ends at a midpoint of an opposing wall or the opposing corner.
- Because of the aforementioned rule, some diagonal lines that bisect a subdivision appear to be thicker that others. This is because they are drawn twice in the same place by the plotter. Below is a good example of this:
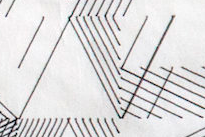
Recreation
SVG:
Screenshot:


I got a bit too invested in this task. It took me about 3 hours of work in Processing and I definitely got pretty close. The most difficult part was creating the triangle line pattern and reversing it for more variety in my output. I was going to recreate the pattern mentioned in observation 7 but I had gassed out at that point. My code is below the read more.
main.pde
import processing.svg.*;
int canvasSize = 800;
int boardSize = 10;
float cellSize = canvasSize/boardSize;
ArrayList cells = new ArrayList();
void settings(){
size(canvasSize, canvasSize);
}
void setup(){
surface.setLocation(50,50);
//background(220);
noFill();
noLoop();
beginRecord(SVG, "output.svg");
}
void generateCells(){
for (Cell c : cells){
c.render();
}
}
void generateBoard(){
for(int i = 0; i < boardSize; i++){
float x = i*cellSize;
for(int j = 0; j < boardSize; j++){
float y = j*cellSize;
cells.add(new Cell(x,y,cellSize));
}
}
}
void draw(){
generateBoard();
generateCells();
endRecord();
}
cell.pde
class Cell{
float x, y, size;
int sub1, sub2;
boolean renderSub2; //needed to check which sub variable for tri pattern
int determineSub(){
//0, 1, 2, 3 for N, E, S, W
return floor(random(4));
}
Cell(float x_, float y_, float size_){
x = x_;
y = y_;
size = size_;
sub1 = determineSub();
sub2 = determineSub();
renderSub2 = false;
}
//RENDERERS
void renderSub(){
switch(sub1){
case 0:
randomPattern(x,y,size,size/2);
break;
case 1:
randomPattern(x+size/2,y,size/2,size);
break;
case 2:
randomPattern(x,y+size/2,size,size/2);
break;
case 3:
randomPattern(x,y,size/2,size);
break;
}
renderSub2 = true;
if(sub1 != sub2){
switch(sub2){
case 0:
randomPattern(x,y,size,size/2);
break;
case 1:
randomPattern(x+size/2,y,size/2,size);
break;
case 2:
randomPattern(x,y+size/2,size,size/2);
break;
case 3:
randomPattern(x,y,size/2,size);
break;
}
}
}
void render(){
push();
noFill();
renderSub();
pop();
}
//HELPERS
int returnCurrentSubVal(){
if(renderSub2) return sub2;
return sub1;
}
//PATTERNS
void randomPattern(float x, float y, float w, float h){
float rand = random(1);
if (rand < 0.5) fullHatch(x,y,w,h); else if (rand > 0.9) tri(x,y,w,h);
else halfHatch(x,y,w,h);
//that random floater
float rand2 = random(1);
if (rand2 > 0.99) line(x,y,x+w,y+h);
}
//full hatching
void fullHatch(float x, float y, float w, float h){
int num = floor(random(8))+1;
boolean reverse = boolean(floor(random(2)));
float xOff= w/num;
float yOff = h/num;
if(reverse){
line(x+w,y,x,y+h);
for(int i = 1; i < num; i++){
float n = i*xOff;
float m = i*yOff;
line(x+w-n, y,x,y+h-m);
line(x+w,y+m,x+n, y+h);
//line(x+w, y+m,x+n, y); incorrect, but useful for later
}
}
else {
line(x,y, x+w, y+h);
for(int i = 1; i < num; i++){
float n = i*xOff;
float m = i*yOff;
line(x+n, y, x+w, y+h-m);
line(x, y+m, x+w-n, y+h);
}
}
}
void halfHatch(float x, float y, float w, float h){
int num = floor(random(8))+1;
boolean reverse = boolean(floor(random(2)));
boolean top = boolean(floor(random(2)));
float xOff= w/num;
float yOff = h/num;
if(reverse){
line(x+w,y,x,y+h);
for(int i = 1; i < num; i++){
float n = i*xOff;
float m = i*yOff;
if (top) line(x+w-n, y,x,y+h-m);
else line(x+w,y+m,x+n, y+h);
//line(x+w, y+m,x+n, y); incorrect, but useful for later
}
}
else {
line(x,y, x+w, y+h);
for(int i = 1; i < num; i++){
float n = i*xOff;
float m = i*yOff;
if (top) line(x+n, y, x+w, y+h-m);
else line(x, y+m, x+w-n, y+h);
}
}
}
void tri(float x, float y, float w, float h){
int num = floor(random(6, 10));
boolean reverse = boolean(floor(random(2)));
float xOff = w/num;
float yOff = h/num;
int currentSubVal = returnCurrentSubVal();
if (reverse){
switch(currentSubVal){
case 0://n
for(int i = 1; i< num; i++){
float n = i*xOff;
float m = i*yOff;
line(x+n, y, x+(w/2)+n/2, y+h-m);
//line(x+w-n, y, x+w-(w/2)-(n/2), y+h-m);
}
break;
case 1: //e
for(int i = 1; i< num; i++){
float n = i*xOff;
float m = i*yOff;
line(x+w-n, y+h-(m/2), x+w, y+h-m);
//line(x+n, y+(h/2)-(m/2), x+w, y+h-m);
}
break;
case 2: //s
for(int i = 1; i< num; i++){
float n = i*xOff;
float m = i*yOff;
line(x+(w/2)-(n/2), y+m, x+w-n, y+h);
//line(x+(w/2)+(n/2), y+m, x+n, y+h);
}
break;
case 3://w
for(int i = 1; i< num; i++){
float n = i*xOff;
float m = i*yOff;
line(x, y+h-m, x+w-n, y+(h/2)-m/2);
//line(x, y+m, x+w-n, y+(h/2)+m/2);
}
break;
}
}
else{
switch(currentSubVal){
case 0://n
for(int i = 1; i< num; i++){
float n = i*xOff;
float m = i*yOff;
line(x+w-n, y, x+w-(w/2)-(n/2), y+h-m);
}
break;
case 1: //e
for(int i = 1; i< num; i++){
float n = i*xOff;
float m = i*yOff;
line(x+n, y+(h/2)-(m/2), x+w, y+h-m);
}
break;
case 2: //s
for(int i = 1; i< num; i++){
float n = i*xOff;
float m = i*yOff;
line(x+(w/2)+(n/2), y+m, x+n, y+h);
}
break;
case 3://w
for(int i = 1; i< num; i++){
float n = i*xOff;
float m = i*yOff;
line(x, y+m, x+w-n, y+(h/2)+m/2);
}
break;
}
}
}
}