Project 07 – (Curves) Futuristic Macaroni

Although a disappointingly small amount of code to show for it, this assignment was a huge challenge. Interpreting the math formulas in order to take intentional creative liberties required a lot of guess work and experimentation. I made many iterations of interactions involving different curves until I came across the epicycloid plane curve and figured I would try to work with it. This whole project for me was just about experimenting which in the end I found really rewarding, I was able to make an almost 3D feeling interactive shape with pretty streamlined code.

sketchDownload
// Assignment 07 - PROJECT 
// Name: Jubbies Steinweh-Adler
// Email: jsteinwe@andrew.cmu.edu
// Class: Section D


var ns = 60; //rotation
var nm = 0.4; //sensitivity of wrarotation
var size = 3;

function setup(){
  createCanvas(600,400);
}


function draw(){ 
  background(0);
  translate(width/2,height/2);
  stroke(250, 230, 0);
  strokeWeight(5);
  fill(0);
  
  var t = 3;
  var a = map(mouseX, 0, width, 1, 7);
  var b = map(mouseY, 0, height, 1, 100);
  var offsetX = width/2 - mouseX;
  var offsetY = height/2 - mouseY;
  
  
  //DRAW SHAPES
    for(let i = 0;i < 60; i++) {
      circle(x1(t+i, a, b) + offsetX, y1(t+i, a, b) + offsetY, 7);
      square(x1(t-i, a, b), y1(t-i, a, b), map(mouseY, 0, height, 0, 30), 3);
      
  }
  

}
function x1(t, a, b) {
  return (a + b) * cos(t/ns) - b * cos((a + b) /b * (t/nm));
}
  function y1(t, a, b) {
  return (a + b) * sin(t/ns) - b * sin((a + b)/b * (t/nm));
}
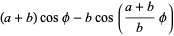
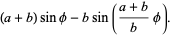
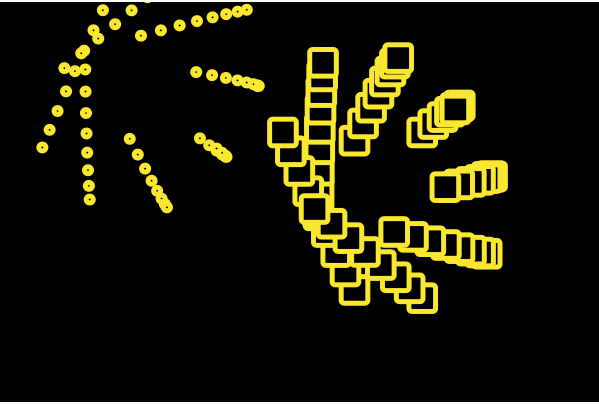
the x and y functions respectively from the Mathworld website (https://mathworld.wolfram.com/Epicycloid.html)

Notice how the columns in the spiral meld into a new column when the shape rotates beyond the rotation capacity! It’s fun to play with : ^)

Leave a Reply