Yoo Jin Shin-Project-07-Curves

Place mouse on canvas!

// Yoo Jin Shin
// Section D
// yoojins@andrew.cmu.edu
// Project-07-Curves


function setup() {
    createCanvas(480, 480);
}

function draw() {
	background(255);

	// Stroke color and weight based on mouseX
	var R = map(mouseX, 0, width, 170, 250);
	var W = map(mouseX, 0, width, 0.3, 1.5);

	push();
	translate(mouseX, mouseY);

	// Gray shadow curve properties
	stroke(240);
	strokeWeight(4); 
	drawCurve2();

	// Colored curve properties
	stroke(R, 200, 200);
	strokeWeight(W);
	drawCurve1();

	pop();
}

// Hypocycloid Pedal Curve (HPC)
function drawCurve1() { 
	var x;
	var y;
	var t = PI;
	var a = map(mouseX, 0, width, 0, 200);
	var n = map(mouseY, 0, height, 0, 10);

	beginShape();
		for(var i = 0; i < width; i++) {
			// HPC equations from Wolfram
			x = a * ((n - 1) * cos(t) + cos((n - 1) * t)) / n
			y = a * ((n - 1) * sin(t) - sin((n - 1) * t)) / n
			vertex(x, y);
			t += 1.3;
		}
	endShape();
}

// HPC Gray Shadow
function drawCurve2() { 
	var x;
	var y;
	var t = PI;
	var a = map(mouseX, 0, width, 0, 200);
	var n = map(mouseY, 0, height, 0, 10);

	beginShape();
		for(var i = 0; i < width; i++) {
			// Same as Curve1, but shifted slightly left/down
			x = a * ((n - 1) * cos(t) + cos((n - 1) * t)) / n - 5;
			y = a * ((n - 1) * sin(t) - sin((n - 1) * t)) / n - 5;
			vertex(x, y);
			t += 1.3;
		}
	endShape();
}

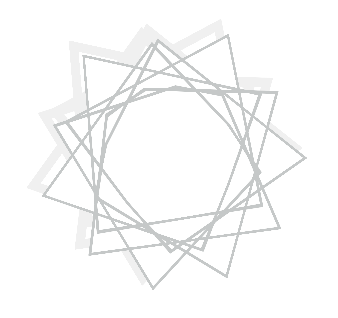
I looked through several different curves on the Wolfram website and ended up choosing the Hypocycloid Pedal Curve. I really liked the range of patterns that it produced when I mapped its properties to the mouse position. I decided to also gradually alter the color and stroke weight (based on the position) for more variety. I tried creating more depth by adding a slightly shifted and faded duplicate of the colored curve, similar to a shadow. Few of the different curves are shown below: