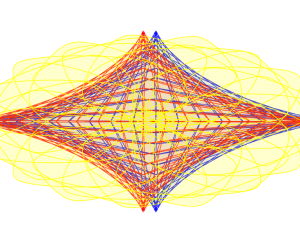
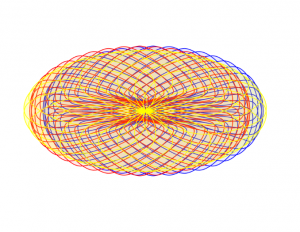
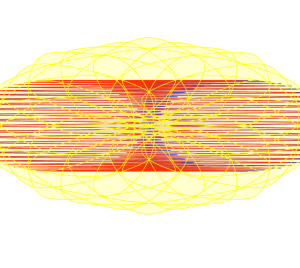
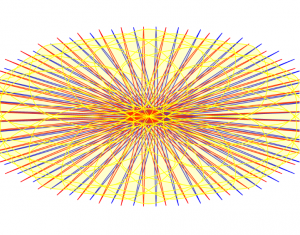
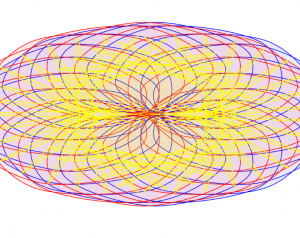
I used a series of three hypocycloid curves (based on the hypocycloid pedal formula) to model an interactive color wheel. I wanted to juxtapose the complex curves and forms with the simplicity of primary colors.
colorwheel
var nPoints = 100 //number of points in each curve
function setup() {
createCanvas(480, 480);
}
function draw() {
var halfWide = width/2
var halfTall = height/2
background('white')
push();
translate(halfWide+10, halfTall) //move center of curves to center of canvas, offset by 10 tp create overlap later
HypocycloidBlueCurve() //draw blue curve
pop();
translate(halfWide-10, halfTall); //move center of curves to center of canvas but offset the other way so overlaps with blue
HypocycloidCurve() //draw red curve
translate(5, 0) //move back to true canvas center to draw yellow curve over both red and blue
HypocycloidYellowCurve() //draw yellow curve
}
function HypocycloidCurve(){
var a1 = constrain(mouseY, 0, 300, 150, 180); //size changes as vertical mouse position changes
var b1 = 45;
var n1 = int(mouseY / 6) //number of cusps of the curve varies with vertical mouse position
stroke('red'); //change stroke color to red
strokeWeight(1);
fill(255, 0, 0, 20); //change fill to transparent red
//create curve, using https://mathworld.wolfram.com/HypocycloidPedalCurve.html base formula for Hypocycloid Pedal Curve
//map points of curve to circle
beginShape();
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var x1 = a1*(((n1-2)*(cos(theta)-cos((1-n1)*theta)))/(2*n1))
var y1 = a1*(((n1-2)*(cos(theta*(1-0.5*n1))*sin(0.5*n1*theta)))/(2*n1))
curveVertex(x1, y1);
}
endShape(CLOSE);
}
//draw blue hypocycloid, same as red but in blue
function HypocycloidBlueCurve(){
var a1 = constrain(mouseY, 0, 300, 150, 180); //size changes as vertical mouse position changes
var b1 = 45;
var n1 = int(mouseY / 6) //number of cusps of the curve varies with vertical mouse position
fill(0, 0, 255, 20) //fill transparent blye
stroke('blue'); //set stroke color to blue
strokeWeight(1);
//create curve, using https://mathworld.wolfram.com/HypocycloidPedalCurve.html base formula for Hypocycloid Pedal Curve
//map points of curve to circle
beginShape();
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var x1 = a1*(((n1-2)*(cos(theta)-cos((1-n1)*theta)))/(2*n1))
var y1 = a1*(((n1-2)*(cos(theta*(1-0.5*n1))*sin(0.5*n1*theta)))/(2*n1))
curveVertex(x1, y1);
}
endShape(CLOSE);
}
//draw yellow hypocycloid
function HypocycloidYellowCurve(){
var a1 = constrain(mouseY, 0, 300, 150, 180); //size changes as vertical mouse position changes
var b1 = 45;
var n1 = int(mouseY / 10) //number of cusps of the curve varies with vertical mouse position
fill(255, 255, 0, 50) //set fill color to a transparent yellow
stroke('yellow'); //set stroke color to yellow
strokeWeight(1);
//create curve, using https://mathworld.wolfram.com/HypocycloidPedalCurve.html base formula for Hypocycloid Pedal Curve
//map points of curve to circle
beginShape();
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var x1 = a1*(((n1-2)*(cos(theta)-cos((1-n1)*theta)))/(2*n1))
var y1 = a1*(((n1-2)*(cos(theta*(1-0.5*n1))*sin(0.5*n1*theta)))/(2*n1))
curveVertex(x1, y1);
}
endShape(CLOSE);
}![[OLD FALL 2020] 15-104 • Introduction to Computing for Creative Practice](wp-content/uploads/2021/09/stop-banner.png)