SectionC – Page 13 – [OLD FALL 2020] 15-104 • Introduction to Computing for Creative Practice

LO 7

*COVID-19* cases across the 50 states over the course of the pandemic

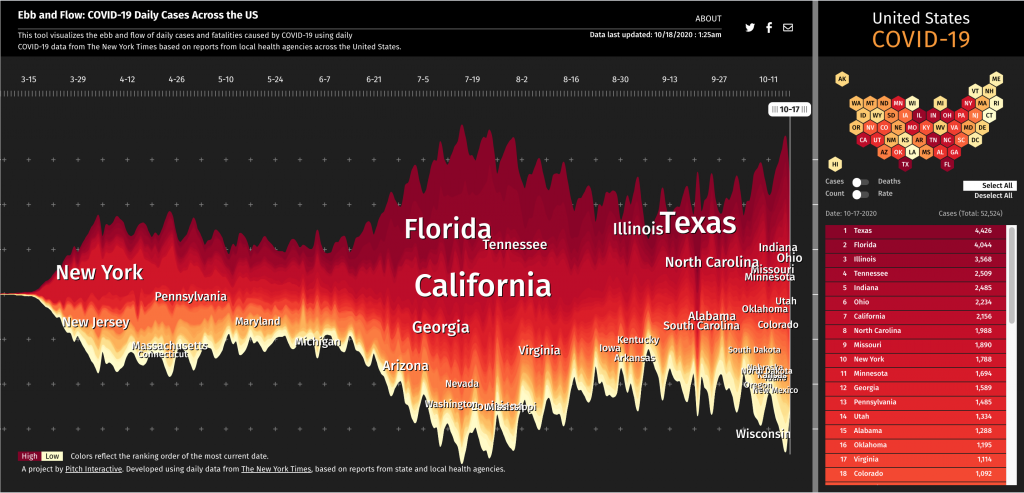
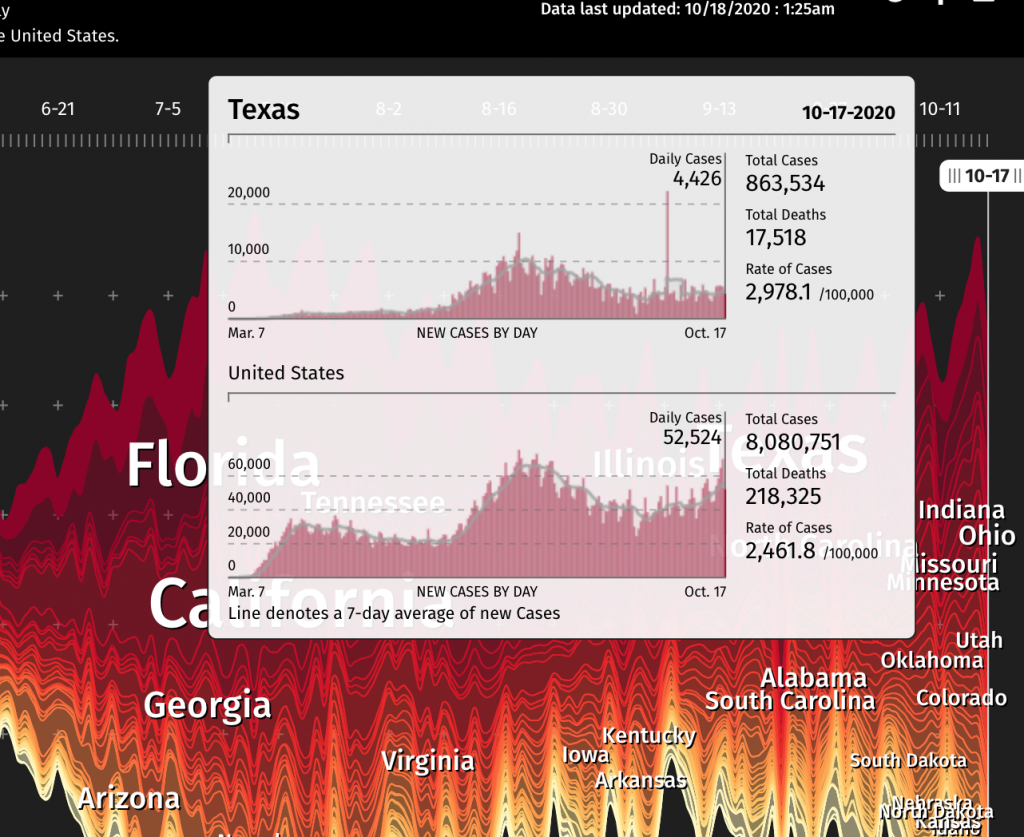
I found Pitch Interactive Inc.’s Ebb and Flow: COVID-19 Daily Cases Across the US a very effective data visualization tool, not to mention very relevant during the pandemic. The tool plots the daily cases and fatalities of each state in the U.S. in relation to each other over the course of the entire pandemic. I think the use of color and the visual nature of the graph effectively instills alertness and demonstrates the severity of the pandemic. As we enter the 7th month of dealing with this public health crisis, the inclusion of all states on the map is essential for the public to access to inspire better community action. People living in states that are doing worse in the current moment will feel a greater sense of responsibility to do better, as they can see their state “called out,” their performance directly plotted against “better” states, and how it affects the holistic curve of the United States. With our country becoming increasingly divided, a tool like this is not only scientifically representative, but has the potential to inspire social and political unity. I find it more effective than the largely achromatic COVID-19 graph provided by Google that forces users to choose their state from a drop-down menu.

Magnifying function displays state’s curve in comparison to the national curve when the user mouses over the state’s curve on the main map

I believe the algorithm is largely determined by some of the functions that made the “stock market tracker” from the last lab, like arrays and array methods like push. Instead of using the noise function to generate the data values, real COVID data from The New York Times would determine the “marketvalue” array. A loop will also hold the array so that it updates daily without manual input. I wouldn’t consider this project to have a lot of artistic considerations, but I do believe the color and other visual decision made make this a good form of communication design made functional with code.

Project 7: Curves

For project 7, I chose to use a logarithmic spiral to create a series of spirals that interact with the mouse position. I was inspired to do logarithmic spirals by some shells I have in a jar on my desk. Then, I wanted to do something that is colored differently than my previous projects.

The spiral’s distance from the center increases or decreases relative to the mouse x position while the degree from the center changes relative to Y depending on the Y position.

sketch

//Helen Cheng
//helenc1@andrew.cmu.edu
//Section C
//Project-07

var theta;
var r;
var nPoints = 500;

function setup() {
  createCanvas(480, 480);
  angleMode(DEGREES);
}

function draw() {
  background(0);
  startAngle = constrain(mouseY, 10,360);
  //parallel spirals
  stroke(255,255,0);
  logSpiral(0,startAngle);
  stroke(255,255,255)
  logSpiral(mouseX, startAngle);
  stroke(255,0,0)
  logSpiral(mouseX+25, startAngle+25);
  stroke(0,255,0)
  logSpiral(mouseX+50, startAngle+50);
  stroke(0,0,255)
  logSpiral(mouseX+75, startAngle+75);

}

function logSpiral(r, theta, color) {
  var x;
  var y;
  noFill();
  beginShape();
  //populates points on each of the spirals
  for (i=0; i<nPoints; i++) {
    x = 240+(r+i)*-cos(theta+2*i);
    y = 240+(r+i)*sin(theta+2*i);
    vertex(x, y);
  }
  endShape();
}

Looking Outwards 7

For this looking outwards assignment, I decided to look at this chart that helped visualize food additives and where they are most commonly found. The reason why I chose this graph is because I’ve always been very health conscious and aware of what goes into my foods. Although I’ve always on and on about how unhealthy snacks can be.

Something that I really like about this work is asides from it’s informational purposes is how it is able to turn data that would normally be a bar chart into something easier to read that can communicate data on quantity on bar thickness like a pie chart but demonstrate the dramatic disproportionate distribution like a pie chart.

I think that they used algorithms that determined thickness as a proportion of the quantity and then just connected the points to the corresponding category.

Looking Outwards 07 – Notabilia

This week I’m discussing Moritz Stefaner’s “Notabilia”, a visual exploration of the most controversial corners of wikipedia. The diagram takes data from Wikipedia’s longest “deletion discussions”: arguments over whether to delete a page or not. Ranging from the absurd – “Object validity of Astrology” – to the hilarious – “List of similarities between Canada and New Zealand”.

Categorized into ‘the deleted’ and ‘the kept’, for whether the article in question was deleted or not, these threads visually show the rough, warped, messy work of distinguishing knowledge from misinformation. The artist managed to represent this highly abstract data in a comprehensible tangle, an impressive management of contradiction that makes it particularly interesting.

-Robert

Project 7 Curves

sketch

var numpoints = 200;

function setup() {
    createCanvas(400, 400);
    frameRate(10);
    noStroke();
}


function draw() {
    background(14,0,54);
    noFill();

    for (i = 1; i < 4; i+=2) { //two left deltoids
    strokeWeight(0.3);
    stroke(201,255,175);
    push();
    translate(width/4,height*i/4);
    deltoid();
    pop();
    }
 
    for (i = 1; i < 4; i+=2) { //two right deltoids
    strokeWeight(0.3);
    stroke(201,255,175);
    push();
    translate(width*3/4,height*i/4);
    deltoid();
    pop();
    }
    
    var c = color(255,202,map(mouseX,0,width,150,225)); // color change for the cornoid
    push();
    strokeWeight(1);
    stroke(c);
    translate(width/2,height/2);
    cornoid();
    pop();
}

function cornoid() {
  var x;
  var y;
  var a = map(mouseX,0,width,100,200); //a value changes according to mouseX, and mapping the value 
  
  beginShape();
  for (var i = 0; i < numpoints; i++ ) {
    var t = map(i, 0, numpoints, mouseY, 200); //theta changes according to the mouseY
    x = a*cos(t)*(1-2*sin(t)*sin(t));
    y = a*sin(t)*(1-2*cos(t)*cos(t));
    rotate(mouseY); //rotating according to mouseY
    vertex(x,y);
  }
  endShape();
}

function deltoid() {
  var x;
  var y;
  var a = map(mouseY,0,height,10,60); //a value changes according to mouseY, and mapping the value 
  
  beginShape();
  for (var i = 0; i < numpoints; i++ ) {
    var t = map(i, 0, numpoints, 0, mouseX); //theta changes according to the mouseX
    x = a/3*(2*cos(t)+cos(t*2));
    y = a/3*(2*sin(t)-sin(t*2));
    rotate(mouseY); //rotating according to mouseY
    vertex(x,y);
  }
  endShape(CLOSE);
}

Looking Outwards 07: Information Visualization

Santiago Ortiz’s Lostalgic was interesting to me. He visualized all the scripts of ABC’s LOST TV show. It is interesting to see how a lot of text is organized and visualized in an interesting format. I like how the text data is translated into interactive visual experience. It is interesting to see heavy data at a glance, and also be able to look closely into the details. I am not sure of what kind of algorithms that generated the work, but I suppose he used some kind of conditionals and loops to organize the data into different episodes and scenes. This work is an interesting experience in which I can read the series in a different, interactive way.

http://intuitionanalytics.com/other/lostalgic/

Project-07: Artistic Curves

I really wanted to create a psychedelic piece with curves. To do this, I made a rainbow effect of colors. The main aspect of the art was a hypotrochoid. This is made with a fixed circle and lines created by another circle rolling along the edge. The piece changes different mathematical aspects of the hypotrochoids based upon the position of the mouse. The curve is created with parametric equations based upon the radius of the fixed circle and the radius of the moving circle. These are the elements that are adjusted with the mouse. The loops created many hypotrochoids and in certain positions on the canvas, this can make very interesting designs.

sketch Download

function setup() {
    createCanvas(480, 480);
    background(220);
    frameRate(20);
}

function draw() {
    background(0);
    //moves the shapes to the center of the canvas
    translate(width/2, height/2);
    for(var i = 0; i<20; i++){
        stroke(random(255), random(255), random(255)); //randomizes colors
        noFill();
        //creates loop of hypotrochoids based upon mouse position
        hypotrochoid(i*mouseX*.5, i*mouseY);
    }
}

//defines the shape hypotrochoid
//https://mathworld.wolfram.com/Hypotrochoid.html
function hypotrochoid(a, mouseY){
    var x; //used for parametric form
    var y; //used for parametric form

    var a; //radius of the fixed circle
    var b = a/10 //radius of the rolling ball
    var h = constrain(mouseY/10, 0, a) //var h depends on mouseY and restricted

    //defines the actual shape
    beginShape();
    for (var i = 0; i < 200; i++){
        var t = map(i, 0, 600, 0, 6*PI);
        x = (a-b)*cos(t)+h*cos(((a-b)/b)*t); //parametric equation for x
        y = (a-b)*sin(t)-h*sin(((a-b)/b)*t); //parametric equation for y
        vertex(x,y);
    }
    endShape(CLOSE);
}

Project 07 Curves

My process for this project was to find a curve I wanted to start with, I started working with a lemniscate and realized I can make flowers out of the infinity symbol. I wanted to make something infinity symbol related but I realized flowers are pretty and work well with the shape. I then made the sizes of the flowers change and the colors change based on the mouseX and mouseY positions.

sketch Download

function setup() {
    createCanvas(480, 480);
}
function draw() {
  background(66,49,148);
  var P=color(mouseX,0,mouseY);    //small flowers
  var R=color(0,mouseX,mouseY);    //big flower
  push();
  fill(P);
  push();
  translate(width/(4/3),height/4);
  scale(.5);
  rotate(radians(45));
  drawCurve();    //small flower top right
  push();
  rotate(radians(90));
  drawCurve();    //small flower top right
  pop();
  pop();
  push();
  translate(width/(4),height/4);
  scale(.5);
  rotate(radians(45));
  drawCurve();    //small flower top left
  push();
  rotate(radians(90));
  drawCurve();    //small flower top left
  pop();
  pop();
  push();
  translate(width/(4/3),height/(4/3));
  scale(.5);
  rotate(radians(45));
  drawCurve();    //small flower bottom right
  push();
  rotate(radians(90));
  drawCurve();    //small flower bottom right
  pop();
  pop();
  push();
  translate(width/(4),height/(4/3));
  scale(.5);
  rotate(radians(45));
  drawCurve();    //small flower bottom left
  push();
  rotate(radians(90));
  drawCurve();    //small flower bottom left
  pop();
  pop();
  pop();
  push();
  fill(R);
  translate(width/2,height/2);
  push();
  drawCurve();   //big flower
  pop();
  push();
  rotate(radians(90));
  drawCurve();    //big flower
  pop();
}

function drawCurve() {
  var a=constrain(mouseX/2,0,width);
  strokeWeight(3.5);
  beginShape();
  var nPoints=360;
  for(var i=0; i<nPoints; i++){
    var t=map(i,0,nPoints,0,PI);    //lemniscate formulas
    x=(a*cos(t))/(1+sin(t)^2);
    y=(a*sin(t)*cos(t))/(1+sin(t)^2);
    vertex(x,y);
  }
  endShape(CLOSE);
  push();
  beginShape();
  scale(.67)
  var nPoints=360;
  for(var i=0;i<nPoints;i++){
    var r=map(i,0,nPoints,0,-PI);    ///other half of lemniscate
    x=(a*cos(r))/(1+sin(r)^2);
    y=(a*sin(r)*cos(r))/(1+sin(r)^2);
    vertex(x,y);
  }
  endShape(CLOSE);
  pop();
}

LO-07: Expression of Elements

Artist: Nicholas Felton
Piece: Elements
Date: 2017-Present

Felton with his piece “Elements” created a better experience for learning. In a concept like the periodic table, many elements are hard to visualize. Felton creates impressive 3D renderings to show what each element looks like in its natural state. Felton described the purpose of this piece is to practice techniques needed to show different states of matter. Additionally, with some elements only having slight differences between one another, the level of detail needed is a good way for him to practice micro-details in renderings. Felton’s artistic sensibilities are shown through the attention to detail and the interpretation of elements that are not easily visualized. The best example is hydrogen. Hydrogen is not an element seen by the human eye, but by utilizing computational tools, Felton was able to create an accurate depiction of the element. The piece also shows the position on the periodic table as well as the electron shells. The artwork not only is creative in its interpretations, but scientifically accurate. Creations like this are improving education and understanding of difficult concepts.

http://feltron.com/Elemental.html

Feltron: Elemental — Visual Representation of Hydrogen

Looking Outwards 07

Nicholas Feltron is an artist who uses code and computation to create his art. This piece I would like to talk about is on his website labeled BikeCycle. It shows a couple of different scenes that focus on the activity, popular routes, stations, bikes, and cyclist demographics within New York city. I admire this piece because I grew up being in the city weekly, it seems very cool to see my second home mapped out via bike schedules and routes. This piece was commissioned by the MoMA store. I am not sure how this dataset was collected and what algorithms were used in the making of this piece. This artist has a variety of computer generated informational art, as this seems to be his main artistic style.

http://feltron.com/BikeCycle.html