// Jisoo Geum
// Section B
// jgeum@andrew.cmu.edu
// Project 11
var tt1;
var startX;
var startY;
var aa;
var ttlength;
function setup() {
createCanvas(480, 400);
background(173, 255, 244);
tt1 = makeTurtle(startX,startY);
tt1.setColor(color(255,144,0));
tt1.setWeight(0.5);
startX = width/2; // set the starting point to center of the canvas
startY = height/2;
aa = random(20,340) // randomise angle
ttlength = random(100,400); // randomize the length of the lines
}
function mousePressed() {
for( var i=0; i <height/4; i +=2){
tt1.penDown();
tt1.forward(ttlength);
tt1.right(aa);
tt1.forward(ttlength);
tt1.penUp();
tt1.goto(startX,startY+i);
}
}
function turtleLeft(d){this.angle-=d;}function turtleRight(d){this.angle+=d;}
function turtleForward(p){var rad=radians(this.angle);var newx=this.x+cos(rad)*p;
var newy=this.y+sin(rad)*p;this.goto(newx,newy);}function turtleBack(p){
this.forward(-p);}function turtlePenDown(){this.penIsDown=true;}
function turtlePenUp(){this.penIsDown = false;}function turtleGoTo(x,y){
if(this.penIsDown){stroke(this.color);strokeWeight(this.weight);
line(this.x,this.y,x,y);}this.x = x;this.y = y;}function turtleDistTo(x,y){
return sqrt(sq(this.x-x)+sq(this.y-y));}function turtleAngleTo(x,y){
var absAngle=degrees(atan2(y-this.y,x-this.x));
var angle=((absAngle-this.angle)+360)%360.0;return angle;}
function turtleTurnToward(x,y,d){var angle = this.angleTo(x,y);if(angle< 180){
this.angle+=d;}else{this.angle-=d;}}function turtleSetColor(c){this.color=c;}
function turtleSetWeight(w){this.weight=w;}function turtleFace(angle){
this.angle = angle;}function makeTurtle(tx,ty){var turtle={x:tx,y:ty,
angle:0.0,penIsDown:true,color:color(128),weight:1,left:turtleLeft,
right:turtleRight,forward:turtleForward, back:turtleBack,penDown:turtlePenDown,
penUp:turtlePenUp,goto:turtleGoTo, angleto:turtleAngleTo,
turnToward:turtleTurnToward,distanceTo:turtleDistTo, angleTo:turtleAngleTo,
setColor:turtleSetColor, setWeight:turtleSetWeight,face:turtleFace};
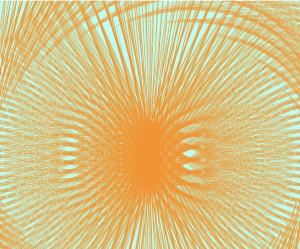
return turtle;}For this project, I wanted to use randomized angles and line lengths to explore different compositions. I also wanted to see shapes created from the repetition and overlaps of thin lines.


![[OLD FALL 2018] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)