Week 5

Nested Loops

sketch

// Getting Started with p5.js
// Lauren McCarthy, Casey Reas, Ben Fry

function setup() {
    createCanvas(600, 400);
    noStroke();
}

function draw() {
    background(0);
    for (var y = 0; y < height+25; y += 50) {
        for (var x = 0; x < width+25; x += 50) {
            fill(255, 140);
            ellipse(x, y, 50, 50);
        }
    }
    noLoop(); // save computation -- no animation
}

Exercise: Rewrite this program so that the loop variables take on the values 0, 1, 2, …. You can use fixed numbers for the number of rows and columns, e.g. 6 columns x 4 rows.

nestedloopsgridoffset

// Getting Started with p5.js
// Lauren McCarthy, Casey Reas, Ben Fry

function setup() {
    createCanvas(480, 120);
}

function draw() {
    background(0);
    fill(255);
    for (var y = 32; y <= height; y += 8) {
        for (var x = 12; x <= width; x += 15) {
            ellipse(x + y, y, 16 - y/10.0, 16 - y/10.0);
        }
    }
    noLoop(); // save computation -- no animation
}

Exercise: Make this image, or something similar:

sketch182

function setup() {
    createCanvas(600, 200);
}

function draw() {
    background(0);
    fill(255);
    for (var y = 0; y <= height; y += 10) {
        for (var x = 0; x <= width; x += 10) {
            var d = y/10;
            ellipse(x + y, y, d, d);
        }
    }
    noLoop(); // save computation -- no animation
}

Click the mouse in this canvas to select what to draw, and move horizontally to change the spacing.

forloops5.js

// FORM+CODE
// Casey Reas and Chandler McWilliams

var option = 1;
function setup() {
    createCanvas(640, 480);
    noFill();
    frameRate(5); // reduce computation 
}

function draw() {
    background(255);
    var density = map(mouseX, 0, width, 20, 50);
    
    if (option == 1) {
        // Option 1: Stitches
        for (var x = 50; x <= width-50; x += density) {
            for (var y = 50; y <= height-50; y+=density) {
                line(x-5, y-5, x+5, y+5);
                line(x+5, y-5, x-5, y+5);
            }
        }
    } 
    else if (option == 2) {
        // Option 2: Perspective
        for (var x = 50; x <= width-50; x += density) {
            for (var y = 50; y <= height-50; y+=density) {
                line(x, y, width/2, height/2);
            }
        }
    } 
    else if (option == 3) {
        // Option 3: Overlapping circles
        for (var x = 50; x <= width-50; x += density) {
            for (var y = 50; y <= height-50; y+=density) {
                ellipse(x, y, 40, 40);
            }
        }
    } 
    else if (option == 4) {
        // Option 4: Rotating arcs
        var count = 120;
        for (var x = 50; x <= width-50; x += density) {
            for (var y = 50; y <= height-50; y+=density) {
                var s = map(count, 120, 0, 0, TWO_PI*2);
                arc(x, y, 14, 14, s, s + PI);
                count--;
            }
        }
    } 
    else if (option == 5) {
        // Option 5: Groups of five
        for (var x = 50; x < width-50; x += density) {
            for (var y = 50; y < height-50; y+=density) {
                //rect(x-10, y-10, 22, 22);
                for (var i = 0; i < 16; i+=4) {
                    line(x + i, y, x + i, y + 12);
                }
                line(x, y, x + 12, y + 12);
            }
        }
    }
}

function mousePressed() {
    option++;
    if (option > 5) option = 1;
}

Function Exercise

Exercise: Take a previous example with nested loops. Replace the inner loop with a call to a function named drawRow, and implement the function.

Return Example

return.js

// Getting Started with p5.js
// Lauren McCarthy, Casey Reas, Ben Fry

function setup() {
    createCanvas(300, 200);
    noStroke();
    frameRate(5);
}

function draw() {
    background(0);
    for (var y = 0; y < height; y += 20) {
        for (var x = 0; x < width; x += 20) {
            fill(0, 200, 0);
            if (nearMouse(x, y)) {
                rect(x, y, 10, 10);
            }
        }
    }
}

function nearMouse(x, y) {
    return dist(x, y, mouseX, mouseY) < 50;
}

// you could also write nearMouse like this:
/*
function nearMouse(x, y) {
    if (distance(x, y, mouseX, mouseY) < 100) {
        return true;
    } else {
        return false;
    }
}
*/

Exercise: Modify the previous example so that nearMouse takes a 3rd parameter which is the distance threshold (which is currently fixed at 50). Make a global variable distThreshold in the program and initialize it to a new distance threshold, say, 30. Use the global variable distThreshold as the third parameter in the call to nearMouse.

Discussion

Imagine that instead of passing a third parameter to nearMouse you just compared the distance to distThreshold and did not add a third parameter.

• Do you think this would this be a better solution?
• When would this not be a better solution?

Sine = Sin, Cosine = Cos, Radius, and Angle

So far, we have talked about expressing locations in terms of X and Y, but you can also describe locations in terms of angle and radius. These are called polar coordinates.

Introducing Sin and Cos

cos and sin functions tell you X and Y coordinates of a point on a circle of radius 1. The input parameter for cos and sin is the angle: How far to rotate around the circle. The output is where you land in terms of X (cos) and Y (sin):

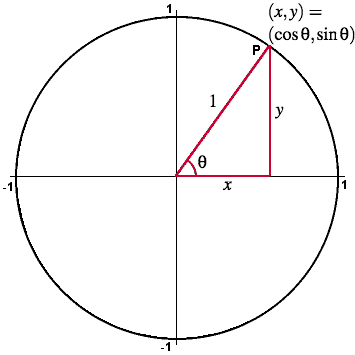
(From “The Amazing Unit Circle”) This shows that the X, Y coordinates can be computed in terms of the angle, represented by θ. Here, θ is a variable representing an angle, “cos θ” means cos(θ), and “sin θ” means sin(θ).

Here’s a graph showing how the functions sin() and cos() translate angle (here represented by the x coordinate) into a value shown as displacement in the Y axis.

sincos

function setup() {
    createCanvas(400, 120);
    noLoop();
}

function draw() {
    background(150, 200, 150);
    for (var x = 0; x < width; x = x + 1) {
        stroke(0);
        point(x, 60 - 50 * sin(radians(x)));
        stroke(255, 255, 0);
        point(x, 60 - 50 * cos(radians(x)));
    }
}

Rotating

Perhaps more interestingly, we can now write a program that creates circular motion by translating radius and angle into X and Y. You should understand how the following program works and why the circle moves in a circle.

Exercise:Make the circle go faster. Make the circle bigger. Make circle orbit bigger. What happens if the radius is zero?

orbit

function setup() {
    createCanvas(200, 200);
    frameRate(30);
}

var gAngle = 45;

function draw() {
    var centerx = width / 2;
    var centery = height / 2;
    var radius = 80;
    background(150, 200, 150);
    var x = cos(radians(gAngle)) * radius;
    var y = sin(radians(gAngle)) * radius;
    stroke(0);
    line(centerx, centery, centerx + x, centery - y);
    noStroke();
    ellipseMode(CENTER);
    ellipse(centerx + x, centery - y, 10, 10);
    gAngle = gAngle + 2;
}

Spirals

Finally, change the previous example as follows:

• Start the radius at 1, but increase the radius for each frame.
• Move the background() call to setup() so it does not erase every frame.
• Remove the line, just draw the circle.
• For this web page version, call background and reset radius after a bunch of draw
  calls.

spiral

function setup() {
    createCanvas(200, 200);
    frameRate(30);
    background(150, 200, 150);
}

var gAngle = 45;
var gRadius = 1;
var gFrameCount = 0;

function draw() {
    var centerx = width / 2;
    var centery = height / 2;
    var x = cos(radians(gAngle)) * gRadius;
    var y = sin(radians(gAngle)) * gRadius;
    noStroke();
    ellipseMode(CENTER);
    ellipse(centerx + x, centery - y, 10, 10);
    gAngle = gAngle + 2;
    gRadius = gRadius + 0.1;
    gFrameCount = gFrameCount + 1;
    if (gFrameCount > 1000) {
        gFrameCount = 0;
        gRadius = 1;
        background(150, 200, 150);
    }
}

The map Function

Dan Shiffman on map function

Rotate and Translate Example

rotate

var angle = 0;

function setup() {
    createCanvas(300, 300);
    frameRate(5);
}

function draw() {
    background(200);
    push();

    translate(width / 2, height / 2);
    fill(0, 200, 0);
    rotate(radians(angle * 0.5));
    rectMode(CENTER);
    rect(0, 0, 100, 100);
    pop();

    push();
    translate(width / 2, height / 2);
    fill(0, 0, 200);
    rotate(radians(angle));
    rectMode(CENTER);
    rect(0, 0, 50, 50);
    pop();

    angle = angle + 4;
}

Exercises: Place the rectangles side-by-side. Make the speed of rotation be controlled by two separate variables. Read the p5.js Reference about the noise() function. Use noise() to compute the angle of one or both rectangles.

Summary

Now you know:

• How to write nested for loops and draw grids and 2-D arrays.
• How to use return statements in functions.
• How to define and use parameters in functions.
• How to use cos/sin to convert from angle and radius to X and Y
• How to use the map function to convert data from one range to another range.