/*Austin Treu
atreu@andrew.cmu.edu
Section B
Project 07*/
var cX = 0, cY = 0, nPoints = 100,
t = 0, up = 0, bot = 0, a = 0, b = 0;
function setup() {
createCanvas(480, 480);
frameRate(10);
}
function draw() {
//fade the background
background(255,255,0,20);
//actual shape
//shape is based upon the devil's curve
//http://mathworld.wolfram.com/DevilsCurve.html
fill('orange');
push();
//center the shape
translate(width/2, height/2);
//scale down to half size
scale(0.5);
//create the shape
beginShape();
//utilize mouse values for a and b
a = mouseX;
b = mouseY;
for (var i = 0; i < nPoints; i++) {
//map t around a full circle
t = map(i, 0, nPoints, 0, TWO_PI);
//calculate points
up = pow(a,2)*pow(sin(t),2)-pow(b,2)*pow(cos(t),2);
bot = pow(sin(t),2) - pow(cos(t),2);
cX = cos(t)*(sqrt(up/bot));
cY = sin(t)*(sqrt(up/bot));
vertex(cX, cY);
}
endShape(CLOSE);
pop();
//accidental spiky thing
stroke('red');
push();
//center the shape
translate(width/2, height/2);
//increase size
scale(25);
//create the shape
beginShape();
//utilize mouse values for a and b
a = mouseX;
b = mouseY;
for (var i = 0; i < nPoints; i++) {
//map t around a full circle
t = map(i, 0, nPoints, 0, TWO_PI);
//calculate points
up = pow(a,2)*pow(sin(t),2)-pow(b,2)*pow(cos(t),2);
bot = pow(sin(t),2) - pow(cos(t),2);
//an incorrect parenthesis can change EVERYTHING!!
cX = cos(t*(sqrt(up/bot)));
cY = sin(t*(sqrt(up/bot)));
vertex(cX, cY);
}
endShape(CLOSE);
pop();
}
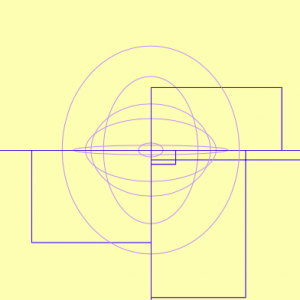
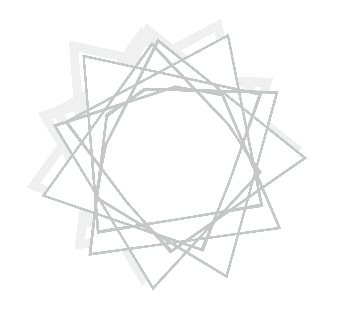
The devil’s curve is what I based this project on. I struggled through this project at the beginning, dealing with a variety of issues that prevented the program from functioning correctly. This was mainly due to two parentheses that were out of place in my math.
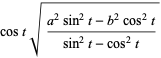
I mistakenly read this as cosine of the quantity of t times the square root as opposed to cosine of t times the quantity of the square root. I did the same for both x and y values. This created the red ‘starburst’ that appears in the middle of the drawing. Once I corrected this, I made a shape correctly based upon the devil’s curve but decided to leave the starburst, as it adds some interesting randomness to the image. Believe it or not, both of the things you see on screen were created with the same equation, only differing by two parentheses and scale.
![[OLD FALL 2018] 15-104 • Introduction to Computing for Creative Practice](../../wp-content/uploads/2020/08/stop-banner.png)