Austin Treu – Project 07

atreu-proj-07

/*Austin Treu
    atreu@andrew.cmu.edu
    Section B
    Project 07*/

var cX = 0, cY = 0, nPoints = 100,
    t = 0, up = 0, bot = 0, a = 0, b = 0;

function setup() {
    createCanvas(480, 480);
    frameRate(10);
}

function draw() {
    //fade the background
    background(255,255,0,20);

    //actual shape
    //shape is based upon the devil's curve
    //http://mathworld.wolfram.com/DevilsCurve.html
    fill('orange');
    push();
    //center the shape
    translate(width/2, height/2);
    //scale down to half size
    scale(0.5);

    //create the shape
    beginShape();
    //utilize mouse values for a and b
    a = mouseX;
    b = mouseY;
    for (var i = 0; i < nPoints; i++) {
        //map t around a full circle
        t = map(i, 0, nPoints, 0, TWO_PI);
        //calculate points
        up = pow(a,2)*pow(sin(t),2)-pow(b,2)*pow(cos(t),2);
        bot = pow(sin(t),2) - pow(cos(t),2);
        cX = cos(t)*(sqrt(up/bot));
        cY = sin(t)*(sqrt(up/bot));
        vertex(cX, cY);
    }
    endShape(CLOSE);
    pop();

    //accidental spiky thing
    stroke('red');
    push();
    //center the shape
    translate(width/2, height/2);
    //increase size
    scale(25);

    //create the shape
    beginShape();
    //utilize mouse values for a and b
    a = mouseX;
    b = mouseY;
    for (var i = 0; i < nPoints; i++) {
        //map t around a full circle
        t = map(i, 0, nPoints, 0, TWO_PI);
        //calculate points
        up = pow(a,2)*pow(sin(t),2)-pow(b,2)*pow(cos(t),2);
        bot = pow(sin(t),2) - pow(cos(t),2);
        //an incorrect parenthesis can change EVERYTHING!!
        cX = cos(t*(sqrt(up/bot)));
        cY = sin(t*(sqrt(up/bot)));
        vertex(cX, cY);
    }
    endShape(CLOSE);
    pop();
}

The devil’s curve is what I based this project on. I struggled through this project at the beginning, dealing with a variety of issues that prevented the program from functioning correctly. This was mainly due to two parentheses that were out of place in my math.

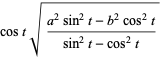
I mistakenly read this as cosine of the quantity of t times the square root as opposed to cosine of t times the quantity of the square root. I did the same for both x and y values. This created the red ‘starburst’ that appears in the middle of the drawing. Once I corrected this, I made a shape correctly based upon the devil’s curve but decided to leave the starburst, as it adds some interesting randomness to the image. Believe it or not, both of the things you see on screen were created with the same equation, only differing by two parentheses and scale.