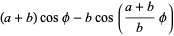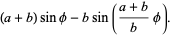Category: SectionD

Project 7: Curves

sketchDownload
var a = 0; //radius of exterior circle
var b = 0; //radius of interior circle
var h = 0; //distance from center of interior circle

var r;
var g;
var b;

var theta = 0; //angle


function setup() {
    createCanvas(500, 500);
    background(220);

}

function draw() {
    r = map(mouseX, 0, width, 45, 191);
    g = map(mouseX, 0, width, 16, 175);
    b = map(mouseY, 0, height, 105, 225);
    background(r, g, b);
    for (var x = 0; x <= width; x += 70) {
        for (var y = 0; y <= height; y += height/5) {
            push();
            translate(x, y);
            drawHypotrochoid();
            pop(); 
        }
    }
}


function drawHypotrochoid() {
    noFill();
    r = map(-mouseX, 0, width, 107, 24);
    g = map(-mouseX, 0, width, 67, 162);
    b = map(-mouseY, 0, height, 67, 162);
    stroke(r, g, b);
    
    a = map(mouseX, 0, width, 1, width/10);
    b = 20;
    h = map(mouseY, 0, height, 1, height/5);
    
    beginShape();
    for (var i = 0; i < 1000; i++) {
        var x = ((a-b) * cos(theta)) + (h * cos((a-b)/b * theta));
        var y = ((a-b) * sin(theta)) - (h * sin((a-b)/b * theta));
        var theta = map(i, 0, 100, 0, TWO_PI);
        vertex(x, y);
    }
    endShape();

}

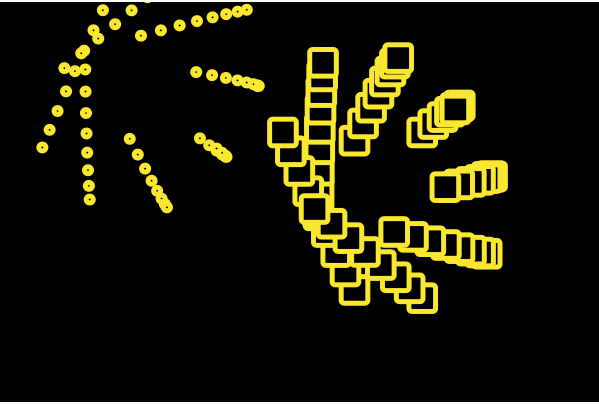
I chose the hypotrochoid curve because when I was experimenting with it, so many different patterns came out of it and I wanted the result to have as many variations as possible. So as you move your mouse up, down, or diagonal, the curve patterns would change every few movements.

Project 07 – Curves

sketch
//TERESA LOURIE
//SECTION D
//PROJECT: INTERACTIVE CURVES
var x = 2;
var y = 2;

function setup() {
    createCanvas(480, 480);
    background(255);
    

}


function draw() {
    background(255);
	
	//figureeight();
	push();
	//for (i=0; i<500; i++){
		
		devilscurve();
	//}
	devilscurve2(); //draw both curves at once on white background
}

function figureeight(){
	push();
	translate(width/2, height/2);

	background(255);
	beginShape();
	stroke(0); 
	strokeWeight(1);
	noFill();

	//loop for curves 
	for(var i =0; i < 750; i++){
		
		stroke(map(mouseY, 0, 480, 0, 255), 0 ,0);
		var t = map(i, 0, 750, 0, 2*PI);
		var a = mouseX;
		var b = 1;
		
		

		x = a*sin(t);
		y = a*sin(t)*cos(t);


		vertex(x, y);
	}
	endShape();
	pop();
}

function devilscurve () { //devils curve function
	push();
	translate(width/2, height/2); //put it in the center
	
	beginShape();     //beginshape, using vertices along the equation
	strokeWeight(3);
	noFill();

	//loop for curves 
	for(var i =0; i < 3000; i++){
		
		stroke(0, 255, map(mouseY, 0, 480, 0, 255));
		var t = map(i, 0, width, -50, 100);
		var a = map(mouseX, 0, width, -50, 10);
		var b = map(mouseY, 0, height, -50, 50);
		
		

		x = cos(t)*sqrt((pow(a, 2)*(t)-pow(b, 2)*pow(cos(t),2)/(pow(sin(t),2)-pow(cos(t),2))));

		y = sin(t)*sqrt((pow(a, 2)*(t)-pow(b, 2)*pow(cos(t),2)/(pow(sin(t),2)-pow(cos(t),2))));
		


		vertex(x, y);
	}
	endShape();
	pop();
}
function devilscurve2 () { //devils curve function
	push();
	translate(width/2, height/2); //put it in the center
	
	beginShape();     //beginshape, using vertices along the equation
	strokeWeight(3);
	noFill();

	//loop for curves 
	for(var i =0; i < 3000; i++){
		
		stroke(255, map(mouseY, 0, 480, 0, 255), 0);
		var t = i
		var a = map(mouseX, 0, width, -50, 100);
		var b = map(mouseY, 0, height, -50, 50);
		
		

		x = cos(t)*sqrt((pow(a, 2)*(t)-pow(b, 2)*pow(cos(t),2)/(pow(sin(t),2)-pow(cos(t),2))));

		y = sin(t)*sqrt((pow(a, 2)*(t)-pow(b, 2)*pow(cos(t),2)/(pow(sin(t),2)-pow(cos(t),2))));
		


		vertex(x, y);
	}
	endShape();
	pop();
}

Project 07 – Curves

The inspiration behind this project was Viviani’s Curve, which is normally contained in 3D space, but can be represented from its front view on the 2D plane as a parabolic curve. I also animated a few circles moving along the curve to give it a bit more life. You can make some pretty interesting shapes, one of which is pictured below.

AAAAAAAAAAAAAAAAAAAAAAAA

function setup() {
    createCanvas(600, 600);
    background(220);
    text("p5.js vers 0.9.0 test.", 10, 15);

    // want to animate circles along curves
    circlePos = 0; // this follows the angle and is a global
}

function draw() {
    background(0);
    var angleIncr = 0.01; // hopefully leads to high definition curve
    var angle = 0;
    var dx, dy;
    var hw = width / 2; // "half width"
    var hh = height / 2;


    beginShape();
    fill(128, 128, 128, 128); // using RGBA
    stroke(128, 128, 128, 128);
    strokeWeight(1);
    // more understandable than using a for loop
    while (angle < 2*PI) {
        // aiming to use Viviani's Curve
        dx = sin(angle);
        dy = 2 * sin(0.5 * angle);

        // want to scale values based on mousePos
        dx *= mouseX - hw;
        dy *= mouseY - hh;

        vertex(dx + hw, dy + hh); // beginShape() doesn't work with translate()
        vertex(-dx + hw, -dy + hh);
        vertex(dy + hw, dx + hh);
        vertex(-dy + hw, -dx + hh);

        // increment angle
        angle += angleIncr;
    }
    endShape();

    angle = 0;
    // second while outside of beginShape()
    while (angle < 2*PI) {
        // aiming to use Viviani's Curve
        dx = sin(angle);
        dy = 2 * sin(0.5 * angle);

        // want to scale values based on mousePos
        dx *= mouseX - hw;
        dy *= mouseY - hh;

        // draw circle
        if (circlePos == angle) {
            fill(mouseX % 255, mouseY % 255, (mouseX + mouseY) % 255);
            circle(dx + hw, dy + hh, 15);
            circle(-dx + hw, -dy + hh, 15);
            circle(dy + hw, dx + hh, 15);
            circle(-dy + hw, -dx + hh, 15);
        }

        angle += angleIncr;
    }

    circlePos = circlePos + angleIncr;
    if (circlePos > 2*PI) circlePos = 0; // can't modulo properly with PI
}

An image captured when the mouse was at the left side of the screen.

LO7 – Information Visualization

The project that caught my eye this week is Chris Harrison’s WordSpectrum. Its purpose is to visualize bigram data to represent word associations. For example, it takes the words “war” and “peace,” and then places words that appear most frequently as bigrams with these from left to right depending on which word they appear next to more. Due to this, you get “war” and “ii” on the same side of the graphic, then you have “peace” and “officers” on the other side. In the center of the graphic you have words that are used generally equally between the two, and because these words are related to each other, most of the time these words will be conjunctions. For example, the word “and” is near the center for most graphics because people have a tendency to write phrases such as “war and peace,” or “good and evil,” leading to high word associations between the two. I find this project particularly interesting because it shows to at least some degree what people associate with certain words, giving a glimpse into the minds.

View post on imgur.com
A screenshot of the graphic for war and peace. Please note that the right side says peace, and the PDF was misbehaving.

Looking Outwards 07

he project I will be discussing for this looking outwards is The Ross Spiral Curriculum from 2015. It was created by Santiago Ortiz and it is an interactive display of a K-12 curriculum. At the center of the spiral is cultural history, and different subjects expand outwards in complexity from that center point. I admire this project because it was created to serve teachers and administrators, so its design is easily readable. It also outlines the material by grade and by time, which allows for digesting the information in whichever manner is most useful. Because you can zoom in and out to view the design as a whole or individual parts and you can click on parts of the design to reach new pieces of information, I know that there is some interactive code involved. The curve of the spiral also makes me think that there is code similar to the code we used for our project this week involved.

Here is a link to the project:

https://spiral.ross.org/spiral/#/

https://spiral.ross.org/spiral/#/

Project 07 Curves

curveDownload
function setup() {
    createCanvas(480, 480);
    background(220);
    text("p5.js vers 0.9.0 test.", 10, 15);
}

function drawAgnesiCurve() {
	var x; //x position of the curve
	var y; //y position of the curve
	var a = mouseX; //honestly not sure what a does
	stroke(max(mouseX, 255), max(mouseY, 255), 0);
	strokeWeight(4);
	beginShape();
	for (var i = 0; i < 65; i++) {
		var t = map(i, 0, 65, 0, TWO_PI);
		x = (2*a)*sin(t);
		y = a*(1-cos(2*t));
		vertex(x, y);
	}
	endShape();
}



function draw() {
	background(0, 0, min(mouseX, mouseY))
	for (var nLine = 0; nLine < 48; nLine++) {
		translate(width/2, 0);
		drawAgnesiCurve();
		translate(0, 10);
	}
}

Project 07 – (Curves) Futuristic Macaroni

Although a disappointingly small amount of code to show for it, this assignment was a huge challenge. Interpreting the math formulas in order to take intentional creative liberties required a lot of guess work and experimentation. I made many iterations of interactions involving different curves until I came across the epicycloid plane curve and figured I would try to work with it. This whole project for me was just about experimenting which in the end I found really rewarding, I was able to make an almost 3D feeling interactive shape with pretty streamlined code.

sketchDownload
// Assignment 07 - PROJECT 
// Name: Jubbies Steinweh-Adler
// Email: jsteinwe@andrew.cmu.edu
// Class: Section D


var ns = 60; //rotation
var nm = 0.4; //sensitivity of wrarotation
var size = 3;

function setup(){
  createCanvas(600,400);
}


function draw(){ 
  background(0);
  translate(width/2,height/2);
  stroke(250, 230, 0);
  strokeWeight(5);
  fill(0);
  
  var t = 3;
  var a = map(mouseX, 0, width, 1, 7);
  var b = map(mouseY, 0, height, 1, 100);
  var offsetX = width/2 - mouseX;
  var offsetY = height/2 - mouseY;
  
  
  //DRAW SHAPES
    for(let i = 0;i < 60; i++) {
      circle(x1(t+i, a, b) + offsetX, y1(t+i, a, b) + offsetY, 7);
      square(x1(t-i, a, b), y1(t-i, a, b), map(mouseY, 0, height, 0, 30), 3);
      
  }
  

}
function x1(t, a, b) {
  return (a + b) * cos(t/ns) - b * cos((a + b) /b * (t/nm));
}
  function y1(t, a, b) {
  return (a + b) * sin(t/ns) - b * sin((a + b)/b * (t/nm));
}
the x and y functions respectively from the Mathworld website (https://mathworld.wolfram.com/Epicycloid.html)

Notice how the columns in the spiral meld into a new column when the shape rotates beyond the rotation capacity! It’s fun to play with : ^)

LO 07 – Data Visualization and WikiRacing

Data Visualization

According to Wikipedia, “Wikiracing is a game using the online encyclopedia Wikipedia which focuses on traversing links from one page to another”. I used to play Wikiracing in high school due to school-provided computer restrictions which severely limited entertainment websites, (3-Clicks-To-Jesus was a popular variation of this game requiring the player to start at a random word and try to reach ‘Jesus’ in – you guessed it – three clicks). When I saw Chris Harrison’s Wikipedia data visualization project, ‘Cluster Ball’, I was immediately reminded of Wikiracing and the intricately woven nature of the Wiki universe. This graphic elegantly depicts the interrelations of wikipedia articles that have a common denominator. As stated in the project description, links between category pages are illustrated by edges, which are color coded to represent their depth from the parent node. Not only would this graphic serve as a handy aid in an intense round of WIkiracing, but it uses simple means to demonstrate how humans communicate and organize language. I admire this work because I think it is surprisingly moving to see how organically the structures of interrelation seem to develop and how every word contributes to and depends upon a greater system of words. The, overwhelming, intricate, and organic architecture and relationships of a single word to a system of words reminds me of ants working together in clearly systematic ways that I don’t quite understand, but can’t help but appreciate the intricacy of.

https://www.chrisharrison.net/index.php/Visualizations/ClusterBall

Project7_curves

sketch_curvesDownload
	// Huijun Shen  session D
    // huijuns@andrew.cmu.edu


var nPoints = 100;
//var lineGroup = [];


function setup() {
    createCanvas(400,400);
    background(180);
    frameRate(10);  
    
}


function draw() {
    background(150);
    noStroke();
    push();
    translate(width/2,height/2);
    rotate(mouseX/30); // make it rotate according to x position
    Orthotomic();
    pop();
    
} 

function Orthotomic(){ //draw the shape

    var x;
    var y;  
    noFill();
    fill(255-mouseY*0.3,mouseY*0.2,100); // make color related to y position
    stroke(3);
   
    beginShape(); // the shape
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        x = constrain(mouseX,0,400)/30*cos(t);
        y = sin(t);
        var x1 =20*(x*cos(2*t)-y*sin(2*t)+2*sin(t));
        var y1 =20*(-x * sin(2*t) - y*cos(2*t) + 2*cos(t));
        vertex(x1+random(5), y1+random(5)); //make the edge a bit random lines
    }


    endShape(CLOSE);    
   
    
}

LO_07_Data Visualization

For this week’s topic, I looked at a chart relating to money- Trillions.

The author is David Macandless, and the source are from New York Times, Bloomberg, UNESCO,WorldBank,Forbes,World Health Organisation, Stanford Uni, Credit Suisse, etc.

Money is a very interesting topic but when the number gets huge, it is very hard to get a real feeling of the amount.

https://informationisbeautiful.net/visualizations/trillions-what-is-a-trillion-dollars/

In this chart, the author raised some very interesting(or not that interesting) topics about what money can do.

By comparing the size of different squares, it is easier to get the idea of how large a concept means or how much money to get one thing to be done.

Among all the topics and comparisons the author can make, those topics shown on the chart silently describe the author’s opinions about some social topics.Also the author secretly implies his/her opinion by gradually changing colors.

I think by visualizing data and deliberately representing data in a certain way, people are easier to get influenced because they tend to think data is object numbers.