/*
Veronica Wang
Section B
yiruiw@andrew.cmu.edu
Project 07
*/
var nPoints = 100;
function setup() {
createCanvas(480, 480);
frameRate(10);
}
function draw() {
background(255);
// draw the curves
push();
translate(width / 2, height / 2);
drawEpitrochoidCurve();
drawHypotrocoidCurve();
pop();
}
//--------------------------------------------------
function drawEpitrochoidCurve() {
// Epicycloid:
// http://mathworld.wolfram.com/Epicycloid.html
var x;
var y;
var a = 60.0;
var b = a / 3.0;
var h = constrain(mouseY / 2, 0, width / 5);
var ph = mouseX / 50.0;
noFill();
stroke('red');
strokeWeight(3);
beginShape();
for (var i = 0; i < nPoints; i++) {
var t = map(i, 0, nPoints, 0, TWO_PI);
x = (a + b) * cos(t) - h * cos(ph + t * (a + b) / b);
y = (a + b) * sin(t) - h * sin(ph + t * (a + b) / b);
vertex(x, y);
}
endShape(CLOSE);
}
function drawHypotrocoidCurve(){
//Hypocycloid
//http://mathworld.wolfram.com/Hypotrochoid.html
var x;
var y;
var a1 = 200;
var b1 = a1 / 3.0;
var h1 = constrain(mouseY / 2, 0, width / 5);
var ph1 = mouseX / 10.0;
noFill();
stroke('red');
strokeWeight(3);
beginShape();
for (var i = 0; i < nPoints; i++) {
var t = map(i, 0, nPoints, 0, TWO_PI);
x = (a1 - b1) * cos(t) + h1 * cos((ph1 + (a1 - b1) / b1) * t);
y = (a1 - b1) * sin(t) - h1 * sin((ph1 + (a1 - b1) / b1) * t);
vertex(x, y);
};
endShape(CLOSE);
}
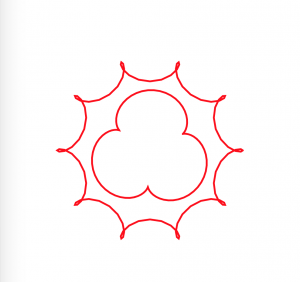
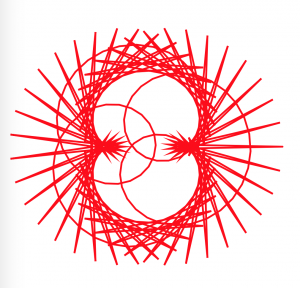
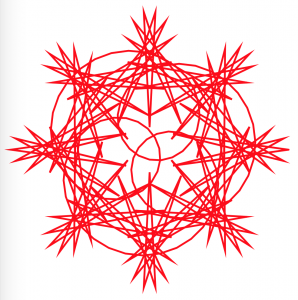
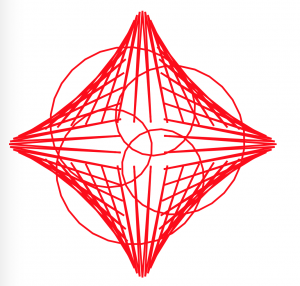
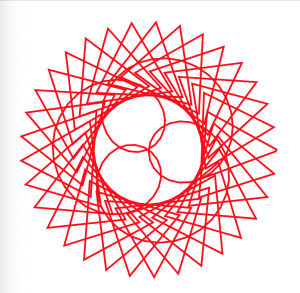
In this project, I used both the hypotrochoid and epitrochoid curves to create interesting compositions. I played around with the amplitude, divisions, diameters, etc of the curve functions. I think it’s interesting how sometimes the animation can sort of explain how the hypotrochoids were generated-when you can see a straight line rotating at the ‘beginning’ point.







![[OLD FALL 2018] 15-104 • Introduction to Computing for Creative Practice](wp-content/uploads/2020/08/stop-banner.png)