//Monica Chang
//mjchang@andrew.cmu.edu
//Section D
//Project-07-Curves
var nPoints = 100;
var radiusX;
var radiusY;
var separation = 125;
function setup() {
createCanvas(480, 480);
}
function draw() {
background("darkcyan");
fill(255, 255, 255, 64);
radiusX = mouseX;
radiusY = mouseY;
drawCircles();
drawEpitrochoidCurve();
drawDeltoid();
}
//circle elements
function drawCircles() {
// a sequence of little, circle elements
push();
translate(width / 2, height / 2);
for (var i = 0; i < nPoints + 10; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var px = radiusX / 2 * cos(theta);
var py = radiusY / 2 * sin(theta);
stroke("lightcyan");
strokeWeight(1);
circle(px - 5, py - 5, 8, 8);
}
pop();
}
function drawDeltoid() {
//Deltoid:
//http://mathworld.wolfram.com/Deltoid.html
beginShape();
nPoints = 40;
for (var i = 0; i < nPoints; i++) {
var angle = map(i, 0, 180, 0, 360);
var radius = 70;
var a = map(mouseX, 0, height, 5, 80)
var b = map(mouseY, 0, height, 5, 90)
//x-coordinate for deltoid
var x = (a - b) * cos(angle) + radius * cos((a - b * angle));
//y-coordinate for deltoid
var y = (a - b) * sin(angle) - radius * sin((a - b * angle));
rotate(radians(angle));
noFill();
strokeWeight(3);
stroke("red");
vertex(x, y);
}
endShape();
}
function drawEpitrochoidCurve() {
// Epicycloid:
// http://mathworld.wolfram.com/Epicycloid.html
var x2;
var y2;
var a = 80.0;
var b = a / 2.0;
var h = constrain(mouseY / 8.0, 0, b);
var ph = mouseX / 30.0;
noFill();
stroke("tan");
strokeWeight(1);
beginShape();
translate(width / 2, height / 2);
for (var i = 0; i < nPoints + 10; i++) {
var t = map(i, 0, nPoints, 0, TWO_PI);
x2 = (a + b) * cos(t) - h * cos(ph + t * (a + b) / b);
y2 = (a + b) * sin(t) - h * sin(ph + t * (a + b) / b);
//switching x and y-coordinates to create a band of waves/
vertex(x2, y2);
vertex(y2, x2);
}
endShape(CLOSE);
}




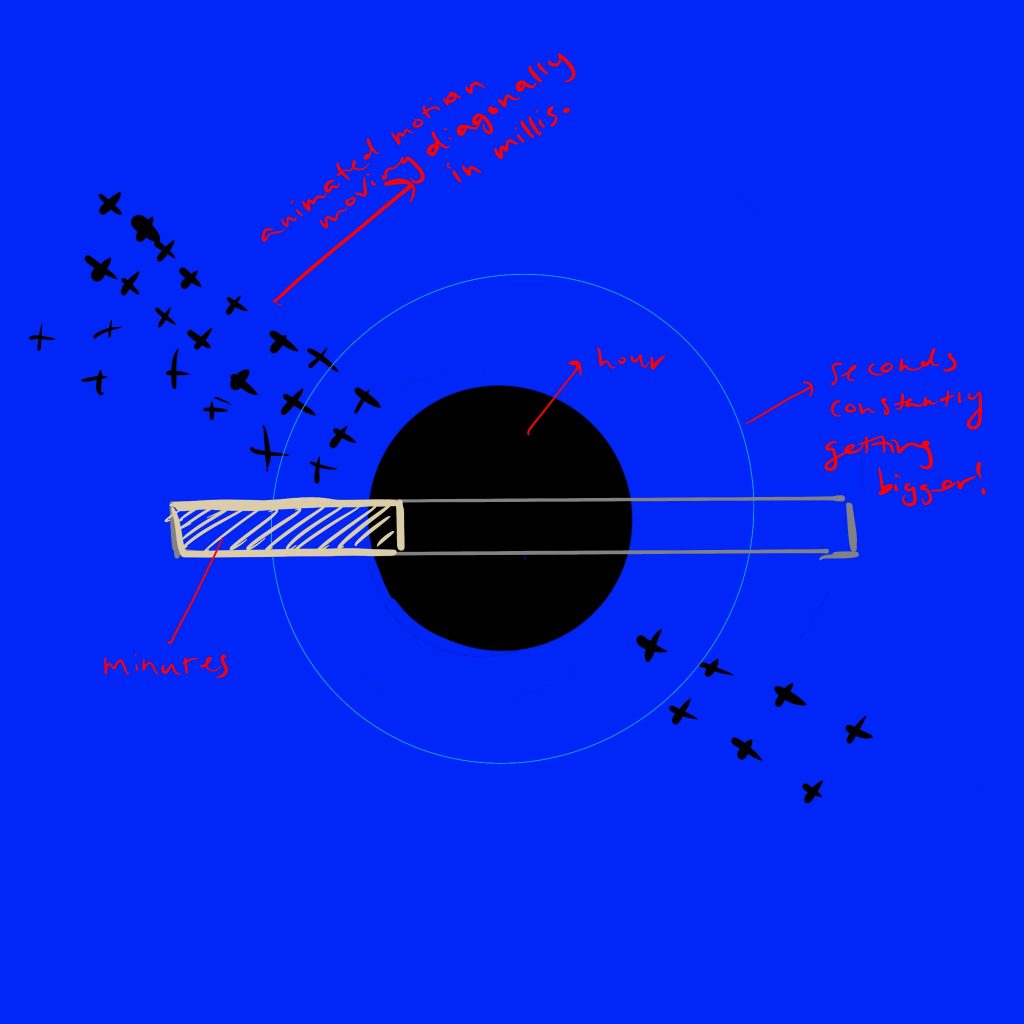
This project definitely had me studying the formulas 75% of the time for me to really start putting anything together. However, once I got the gist of the formulas, it was really entertaining for me. I began with studying the deltoid curve and I realized this particular curve created so many different shapes. Thus, I wanted to provide a more constant curve which became the sequence of circles which are relatively more static to create a sense of balance.
![[OLD FALL 2019] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)