//Lanna Lang
//Section D
//lannal@andrew.cmu.edu
//Project 07 - Curves
var nPoints = 100;
var angle = 0;
function setup() {
createCanvas(480, 480);
}
function draw() {
background('#ffc5a1'); //pastel orange
//call, translate, and rotate
//the epitrochoid curve
push();
translate(width/2, height/2);
rotate(radians(angle));
drawEpitrochoid();
angle += 10;
pop();
//call and translate the hypotrochoid curve
push();
translate(width/2, height/2);
drawHypotrochoid();
pop();
}
//Epitrochoid curve (biggest curve)
function drawEpitrochoid() {
//http://mathworld.wolfram.com/Epitrochoid.html
var x1;
var y1;
//scale and rotation based on mouseY and mouseX
var a1 = map(mouseY, 0, 480, 10, 70);
var b1 = 20;
var h1 = mouseX;
strokeWeight(4);
stroke('lightyellow');
fill(mouseX, 150, mouseY); //fill based on the mouse
beginShape();
for (var i = 0; i < nPoints; i++) {
var t1 = map(i, 0, nPoints, 0, TWO_PI);
//epitrochoid equation
x1 = (a1 + b1) * cos(t1) - (h1 * cos((a1 + b1 / b1) * t1));
y1 = (a1 + b1) * sin(t1) - (h1 * sin((a1 + b1 / b1) * t1));
vertex(x1, y1);
}
endShape(CLOSE);
}
//Hypotrochoid curve
function drawHypotrochoid() {
//http://mathworld.wolfram.com/Hypotrochoid.html
//rainbow filled hypotrochoid
var x2;
var y2;
//scale and rotation based on the mouse
var a2 = map(mouseY, 0, 480, 80, 200);
var b2 = 20;
var h2 = mouseX / 10;
strokeWeight(4);
stroke('hotpink');
fill(mouseX, mouseY, 200);
beginShape();
for (var i = 0; i < nPoints; i++) {
var t2 = map(i, 0, nPoints, 0, TWO_PI);
//hypotrochoid equation
x2 = (a2 - b2) * cos(t2) + h2 * cos((a2 - b2) / b2 * t2);
y2 = (a2 - b2) * sin (t2) - h2 * sin((a2 - b2) / b2 * t2);
vertex(x2, y2);
}
endShape(CLOSE);
//green hypotrochoid with lines
var x3;
var y3;
var a3 = 180;
var b3 = map(mouseY, 480, 0, 180, 20);
var h3 = -mouseX / 10;
//array for the lines inside the curve
var lineX = [];
var lineY = [];
strokeWeight(3);
stroke('lightgreen');
noFill();
beginShape();
for (var i = 0; i < nPoints; i++) {
var t3 = map(i, 0, nPoints, 0, TWO_PI);
//hypotrochoid equation
x3 = (a3 - b3) * cos(t3) + h3 * cos((a3 - b3) / b3 * t3);
y3 = (a3 - b3) * sin(t3) - h3 * sin((a3 - b3) / b3 * t3);
vertex(x3, y3);
lineX.push(x3);
lineY.push(y3);
}
endShape(CLOSE);
//draw the lines inside the curve with a for loop
for (var i = 0; i < lineX.length - 1; i++) {
strokeWeight(2);
stroke(mouseX + mouseY, mouseY, 120);
line(0, 0, lineX[i], lineY[i]);
}
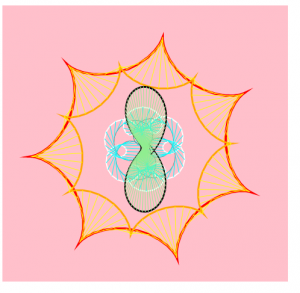
}I was intimidated at first looking at the instructions that said we had to create an image based on math curve functions, and I thought it would be very difficult to do, but it turned out to be pretty simple. I had a lot of fun researching the different roulette curves and seeing which ones did cool things with code. I played a lot with mouseX and mouseY, as well as scale, map(), and color. My favorite part of this project is that if you stop your mouse at a different point on the canvas, the epitrochoid curve changes into a completely different curve each time; it’s so interesting to see the crazy curves it can create by changing its a, b, and h values with the mouse’s coordinates.


![[OLD FALL 2019] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)