//Ankitha Vasudev
//ankithav@andrew.cmu.edu
//Section B
//Project 07
//global variable
var nPoints = 600;
function setup() {
createCanvas(450, 450);
frameRate(100);
}
function draw() {
background(0);
//variables to change stroke color depending on mouse position
var r = map(mouseX, 0, width, 50, 255);
var g = map(mouseX, 0, width, 50, 255);
var b = map(mouseY, 0, height, 50, 255);
noFill();
//calling Hypotrochoid function
push();
stroke(r, g, b);
strokeWeight(0.15);
translate(width/2, height/2);
drawHypotrochoid();
pop();
//calling Astroid function
push();
stroke(g, b, r);
strokeWeight(0.15);
translate(width/2, height/2);
drawAstroid();
pop();
}
function drawHypotrochoid() {
var x;
var y;
var h = width/2;
//Mouse controls radius of hyportochoid
var a = map(mouseX, 0, width, 0, width/100);
var b = map(mouseY, 0, height, 0, height/200);
beginShape();
for (var i = 0; i < nPoints; i++) {
var angle = map(i, 0, 180, 0, 360);
//using formula for Hypotrochoid
//mathworld.wolfram.com/Hypotrochoid.html
x = (a - b) * cos(angle) + h * cos((a - b) * angle);
y = (a - b) * sin(angle) - h * sin((a - b) * angle);
vertex(x, y);
}
endShape();
}
function drawAstroid() {
var x;
var y;
//Mouse controls radius of Astroid
var a = map(mouseX/2, 0, width, 0, width/5);
var b = map(mouseY/2, 0, height, 0, height/10);
beginShape();
for (var i = 0; i < nPoints/2; i++) {
var angle = map(i, 0, 100, 0, 360);
//using formula for Astroid/Hypocycloid
//mathworld.wolfram.com/Hypocycloid.html
x = (a - b) * cos(angle) - b * cos(angle * (a - b));
y = (a - b) * sin(angle) - b * sin(angle * (a - b));
vertex(x, y);
}
endShape();
}This project was the most difficult one so far because it took me a while to understand how to draw the curves the way I wanted them to be. I had to look at some online videos to get a better understanding. Additionally, reading the explanations behind the curve equations on Mathworld helped a lot. I played around with the variables and curve layers before finalizing on a Hypotrochoid and Astroid curve. However, the equation for an astroid was too complex so my curve uses a general Hypocycloid equation.
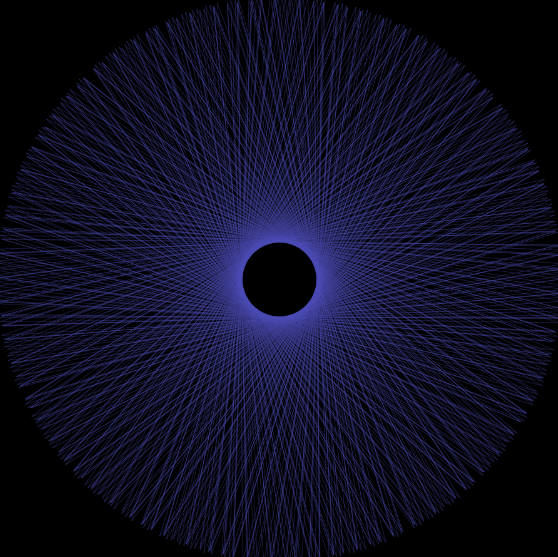
Hypotrochoid curve 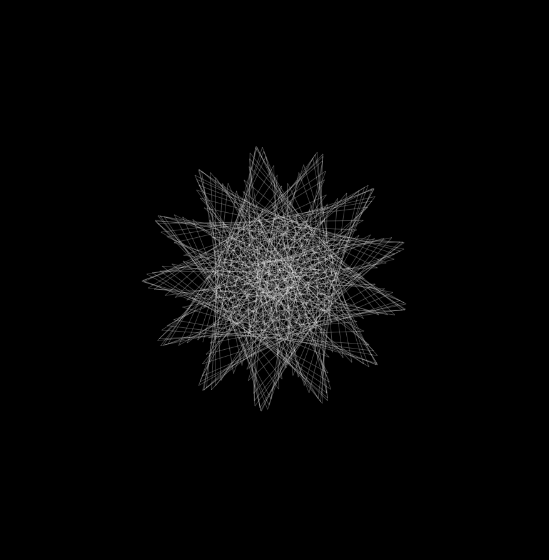
Hypocycloid curve

![[OLD FALL 2019] 15-104 • Introduction to Computing for Creative Practice](wp-content/uploads/2020/08/stop-banner.png)