sketch/*
* Amy Lee
* amyl2
* Section B
*/
// Array variables for star X and Y positioning
var starX = [];
var starY = [];
var r = 5;
var r2 = 10;
var nPoints = 5;
var nPoints2 = 10;
var separation = 120;
function setup() {
createCanvas(480,480);
// Random placement of stars
for (i = 0; i < 60; i++){
starX[i] = random(10,470);
starY[i] = random(10,470);
}
frameRate(7);
}
function draw() {
background(10);
// Time variable for stars
var s = second();
// Setting randomGaussian ellipses in the background
push();
translate(width/2,height/2);
for (var i = 0; i < 1000; i++){
fill(255);
ellipse(randomGaussian(0,120),randomGaussian(0,120),2.2,2.2);
}
pop();
// New star every second
for( i = 0; i < s; i++){
fill(255);
ellipse(starX[i],starY[i],4,4);
}
// Calling on Hypotrochoid Function
push();
noStroke();
translate(width/2,height/2);
drawHypotrochoid();
pop();
// Calling on Ranuculus Function
drawRanuculus();
// Drawing hidden alien, only appears when mouse distance from center is < 50
push();
for(var y = 200; y < 280; y += 5){
for (var x = 200; x < 280; x += 5){
noStroke();
fill(173,212,173);
if(nearMouse(x,y) == true){
// Face
ellipse(241,240,70,70);
// Eye
fill(255);
ellipse(241,240,40,40);
// To make eye follow mouseX when mouseX is near
fill(173,212,173); // green iris
if (mouseX < 256 & mouseX > 230){
ellipse(mouseX,240,25,25);
} else {
ellipse(241,240,25,25);
}
// Pupil
fill(0)
if (mouseX < 256 & mouseX > 230){
ellipse(mouseX,240,20,20);
} else {
ellipse(241,240,20,20);
}
fill(255);
ellipse(248,230,10,10);
}
}
}
pop();
}
function drawHypotrochoid() {
// Setting Hypotrocoid Variables
for (var t = 0; t < 360; t++){
var h = map(mouseY, 0, height/4, height/2, height/4);
var a = 150;
var b = map(mouseY,0,height/2,1,2);
var x = (((a-b)*cos(radians(t))) + h*cos(((a-b)/b)*radians(t)));
var y = (((a-b)*sin(radians(t))) - h*sin(((a-b)/b)*radians(t)));
// Draw pentagons
beginShape();
for (var i = 0; i < nPoints; i++) {
noStroke();
// Pentagons change color as mouseY changes
if (mouseY <= 80){
fill(255,142,157); //Red
} else if (mouseY > 80 & mouseY <= 160){
fill(255,210,142); // Orange
} else if (mouseY > 160 & mouseY <= 240){
fill(255,252,142); // Yellow
} else if (mouseY > 240 & mouseY <= 320){
fill(192,255,142); // Green
} else if (mouseY > 320 & mouseY <= 400){
fill(142,188,255); // Blue
} else if (mouseY > 400 & mouseY <= 480){
fill(157,142,255); // Purple
} else {
fill(random(255),random(255),random(255));
}
// Setting variables for pentagons
var theta = map(i, 0, nPoints, 0, TWO_PI);
var px = r * cos(theta);
var py = r * sin(theta);
// Draw pentagon shape with random jitter
vertex(x+px + random(-1, 1), y+py + random(-1, 1));
}
endShape(CLOSE);
}
}
function drawRanuculus() {
push();
translate(2 * separation, height/2);
// Setting stroke colors according to how mouseY changes
if (mouseY <= 80){
stroke(255,142,157); //Red
} else if (mouseY > 80 & mouseY <= 160){
stroke(255,210,142); // Orange
} else if (mouseY > 160 & mouseY <= 240){
stroke(255,252,142); // Yellow
} else if (mouseY > 240 & mouseY <= 320){
stroke(192,255,142); // Green
} else if (mouseY > 320 & mouseY <= 400){
stroke(142,188,255); // Blue
} else if (mouseY > 400 & mouseY <= 480){
stroke(157,142,255); // Purple
} else {
stroke(random(255),random(255),random(255));
}
strokeWeight(3);
fill(10);
beginShape();
for (var i = 0; i < nPoints2; i += 0.1){
var px2 = r2 * (6 * cos(i) - cos(6 * i));
var py2 = r2 * (6 * sin(i) - sin(6 * i));
vertex(px2, py2);
}
endShape();
pop()
}
function nearMouse(x,y){
if(dist(x,y,mouseX,mouseY) < 50){
return true;
} else {
return false;
}
}
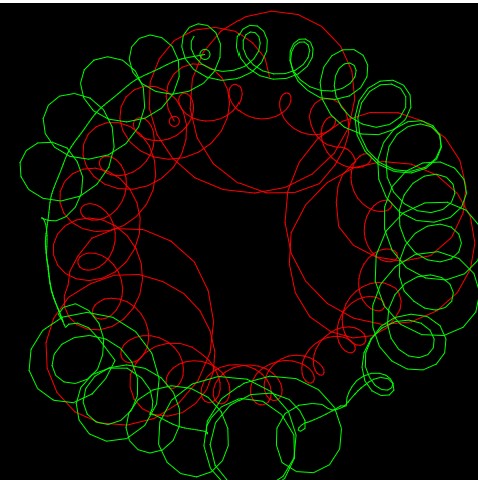
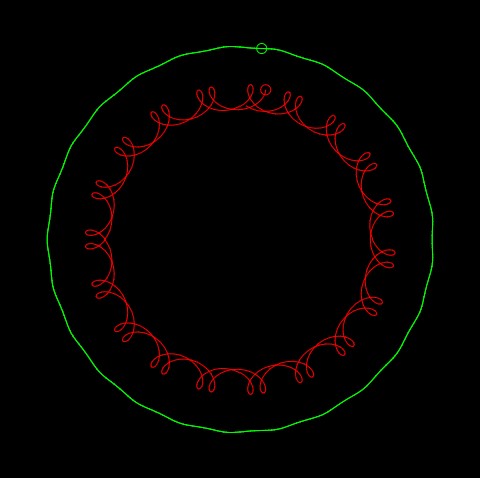
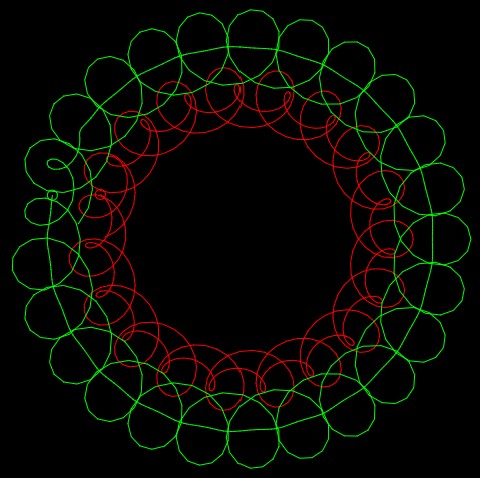
For this project, I played around with the Hypotrochoid and Ranuculus curves to create these designs. I wanted to give this an outer space feel, so I also added a Gaussian distribution of ellipses to resemble stars in the background. When the distance of the mouse is close to the center, an alien eye is revealed. The colors of the curves according to the mouseY position and an additional larger star is added every second. It definitely has a chaotic look to it but I thought that it fit the theme since space is far from organized.

![[OLD FALL 2020] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2021/09/stop-banner.png)