//Christine Kim
//Section A (9:00)
//haewannk@andrew.cmu.edu
//Project-07
var angle;
var X;
var a =300;
var nPoints = 10000;
var g;
var s;
function setup() {
createCanvas(800,800);
frameRate(10);
}
function draw() {
background(91,g,221); //background color mapped to give gradient effect as mouse is moved in X directoin
X=constrain(mouseX,0,width);
Y=constrain(mouseY,0,height);
angle = map(X,0,width,0,2*TWO_PI); //remapping the angle to make it move as mouse moves in X direction
g = map(X,0,width,84,238); //color g mapped for gradient color
s = map(Y,0,height,1,2); //scale variable mapped to change scale of the curves as mouse is moved in Y direction
//first Eight Curve
stroke(255); //color white
strokeWeight(2);
push();
translate(width/2, height/2);
rotate(angle); //rotating by the mapped angle
beginShape(LINES); //creating the Eight Curve
for (var i=0;i<=nPoints; i++) {
var t= map(i,0,nPoints,0,TWO_PI);
//Eight Curve formula
var x2= a*sin(t);
var y2= a*sin(t)*cos(t);
vertex(x2,y2);
}
endShape(CLOSE);
pop();
//second Eight Curve
stroke("#ec96a4"); //color light pink
strokeWeight(2);
push();
translate(width/2, height/2);
scale(s); //scaling by the mapped scale
rotate(angle+QUARTER_PI);
beginShape(LINES);
for (var i=0;i<=nPoints; i++) {
var t= map(i,0,nPoints,0,TWO_PI);
var x2= a*sin(t);
var y2= a*sin(t)*cos(t);
vertex(x2,y2);
}
endShape(CLOSE);
pop();
//third Eight Curve
stroke("#e6df44"); //color mustatd
push();
translate(width/2, height/2);
scale(s);
rotate(-angle+HALF_PI);
beginShape(LINES);
for (var i=0;i<=nPoints; i++) {
var t= map(i,0,nPoints,0,TWO_PI);
var x2= a*sin(t);
var y2= a*sin(t)*cos(t);
vertex(x2,y2);
}
endShape(CLOSE);
pop();
//fourth Eight Curve
stroke("#283655"); //color indigo
strokeWeight(2);
push();
translate(width/2, height/2);
rotate(-angle*2);
beginShape(LINES);
for (var i=0;i<=nPoints; i++) {
var t= map(i,0,nPoints,0,TWO_PI);
var x2= a*sin(t);
var y2= a*sin(t)*cos(t);
vertex(x2,y2);
}
endShape(CLOSE);
pop();
}
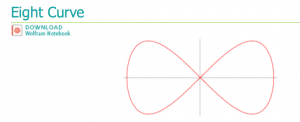
I based my whole project on the Eight Curve and played with color gradient and rotation of the curves.
![[OLD – FALL 2016] 15-104 • COMPUTING for CREATIVE PRACTICE](wp-content/uploads/2020/08/stop-banner.png)