sketch
//Naomi Shimada
//Section D
//nshimada@andrew.cmu.edu
//Project-07
var Y_AXIS = 1;
var X_AXIS = 2;
var Xpos;
var Ypos;
var r;
var t;
var b1, b2, c1, c2; //p5js
var rColor = 255;
var gColor = 255;
var bColor = 255;
function setup() {
createCanvas(600, 600);
//Defines the colors, p5js
b1 = color(255);
b2 = color(0);
c1 = color(204, 102, 0);
c2 = color(0, 102, 153);
}
function draw() {
background(150);
setGradient(0, 0, width/2, height, b1, b2, X_AXIS); //sets background color p5js
setGradient(width/2, 0, width/2, height, b2, b1, X_AXIS); //sets background color p5js
if(mouseX<width/3){
rColor = map(random(0,255),mouseX,0,width/3,0); //makes it flash if mouseX in first third
}
if(mouseX>2*width/3){
gColor = map(random(0,255),mouseX,0,width/3,0); //makes it flash if mouseX in last third
}
if(mouseIsPressed){
rColor = random(0,255);
gColor = random(0,255); //changes the color randomly when the mouse is clicked
bColor = random(0,255);
}
stroke(rColor,gColor,bColor);
drawcurve(width/2, height/2);
}
function drawcurve(x, y) {
push()
translate(x, y); //centers
beginShape();
for (var i = 0; i < 600; i++) { //creates the number of verticies
t = map(i, 0, mouseX, 0, PI); //creates theta
r = 150 * mouseY * tan(t*100) ; //the equation and makes r
Xpos = r * sin(t); //the equation to define the x position
Ypos = r * cos(t); //the equation to define the y position
vertex(Xpos,Ypos); //center of the shape
}
endShape();
pop();
}
function setGradient(x, y, w, h, c1, c2, axis) { //from p5js
noFill();
if (axis == Y_AXIS) { // Top to bottom gradient
for (var i = y; i <= y+h; i++) {
var inter = map(i, y, y+h, 0, 1);
var c = lerpColor(c1, c2, inter);
stroke(c);
line(x, i, x+w, i);
}
}
else if (axis == X_AXIS) { // Left to right gradient
for (var i = x; i <= x+w; i++) {
var inter = map(i, x, x+w, 0, 1);
var c = lerpColor(c1, c2, inter);
stroke(c);
line(i, y, i, y+h);
}
}
}
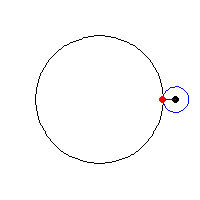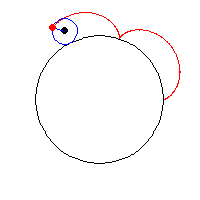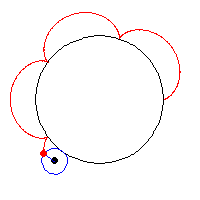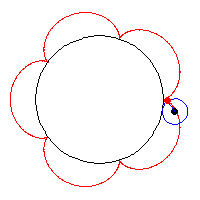
I started browsing the Mathworlds curve site to start my program. Most of them were too complicated for me to understand but I finally found one and then asked a math major to explain it to me and two fellow programmers to help me so I would know how to incorporate the equation into my code. After that I just added in some constants,had the mouseX position dictate whether or not the colors flashed, made the color change if the mouse is pressed, and mapped different parameters to the mouseX and mouseY positions.
![[OLD – FALL 2016] 15-104 • COMPUTING for CREATIVE PRACTICE](../../wp-content/uploads/2020/08/stop-banner.png)