/* Anthony Ra
Section-A
ahra@andrew.cmu.edu
Project-07 */
function setup() {
createCanvas(480, 480);
frameRate(100);
}
function draw() {
background(255);
/* mapping the colors so that it changes based on mouseX */
var r = map(mouseX, 0, width, 140, 180);
var g = map(mouseX, 0, width, 160, 190);
/* printing hypotrochoid */
push();
stroke(r, g, 255);
strokeWeight(0.25);
translate(width/2, height/2);
drawHypotrochoid();
pop();
}
function drawHypotrochoid() {
/* naming variables */
var hypoX;
var hypoY;
/* radius of hypotrochoid */
var hypoRadius = 240;
/* hypotrochoid alteration with cursor */
var a = map(mouseX, 0, width, 0, 5);
var b = map(mouseY, 0, height, 0, 3);
beginShape();
for(var i = 0; i < 300; i ++) {
var angle = map(i, 0, 200, 0, 360);
/* equation of hypotrochoid from the link */
hypoX = (a - b) * cos(angle) + hypoRadius * cos((a - b) * angle);
hypoY = (a - b) * sin(angle) - hypoRadius * sin((a - b) * angle);
vertex(hypoX, hypoY);
}
endShape();
}
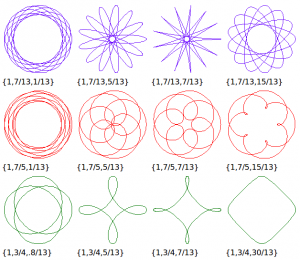
Thinking about the project that we did a couple weeks ago on string art, I focused on curves that bring lightness, tranquility, and balance in regards to symmetry and motion. The purpose of picking a hypotrochoid is the many ways in which the control points of each line or curve responds differently but respects the symmetry in balance.

Looking back at the hypotrochoid chart, that moment of the cursor provides the twelfth iteration, producing a modular set of filleted triangular curves.


![[OLD FALL 2018] 15-104 • Introduction to Computing for Creative Practice](wp-content/uploads/2020/08/stop-banner.png)