![[OLD FALL 2019] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)
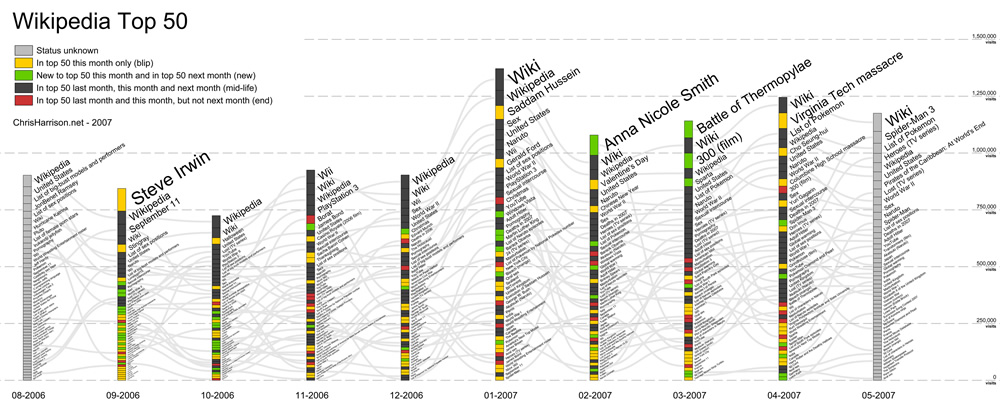
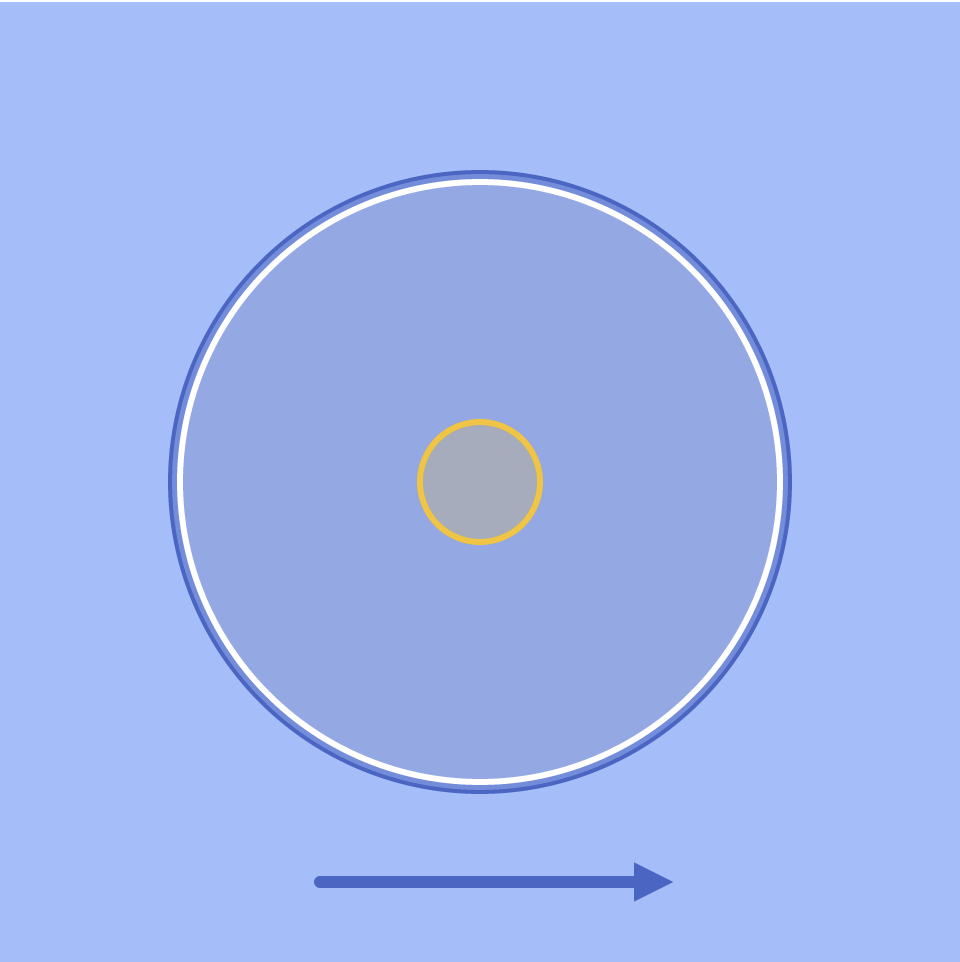
Slowly move the mouse across the canvas (from L to R) to watch the circle transform into a flower!
// Timothy Liu
// 15-104, Section C
// tcliu@andrew.cmu.edu
// OpenProject-07
var nPoints = 1000; // number of points in each function. The more points, the smoother the function is.
// variables for white quadrifolium
var k;
var n;
var d;
// variables for blue quadrifolium
var k2;
var n2;
var d2;
// variables for flower center
var k3;
var n3;
var d3;
function setup() {
createCanvas(480, 480);
frameRate(30);
}
function draw() {
background(160, 190, 255); // light blue background
k = n / d; // k constant determines the number of petals on the white quadrifolium
k2 = n2 / d2; // k constant determines the number of petals on the blue quadrifolium
k3 = n3 / d3; // k constant determines the number of petals on the flower center
arrow(); // drawing in the arrow function
quadrifolium2(); // drawing in the blue flower underneath first
quadrifolium(); // drawing in the white flower on top
flowerCenter(); // drawing in the yellow center on top of the other two flowers
}
// the white flower/quadrifolium
function quadrifolium() {
// these variables/constraints hold mouseX to the width of the canvas
// mouseX1 slows down the speed of mouseX
var mouseX1 = mouseX / 5;
var mouseMove = constrain(mouseX1, 0, width / 5);
// these variables/constants help determine the location of the flower via the equation and vertex
var r;
var x;
var y;
// n and d help determine the k constant, or the number of petals on the flower
n = map(mouseMove, 0, width, 0, 36);
d = 4;
// a determines the size of the white petals
var a = 150;
// white flower colors
stroke(255, 255, 255);
strokeWeight(3);
fill(255, 255, 255, 60);
// drawing the white quadrifolium!
beginShape();
for (var i = 0; i < nPoints; i++) {
var t = map(i, 0, nPoints, 0, TWO_PI * d); // determines theta (the angle)
r = a * cos(k * t); // the equation that draws the quadrifolium
x = r * cos(t) + width / 2; // these help compute the vertex (x, y) using the circular identity
y = r * sin(t) + width / 2;
vertex(x, y);
}
endShape();
}
// the blue flower/quadrifolium
function quadrifolium2() {
// these variables/constraints hold mouseX to the width of the canvas
// mouseX2 slows down the speed of mouseX
var mouseX2 = mouseX / 5;
var mouseMove2 = constrain(mouseX2, 0, width / 5);
// these variables/constants help determine the location of the flower via the equation and vertex
var r2;
var x2;
var y2;
// n2 and d2 help determine the k2 constant, or the number of petals on the flower
n2 = map(mouseMove2, 0, width, 0, 72);
d2 = 6;
// a2 determines the size of the blue petals (slightly longer than the white)
var a2 = 155;
// blue flower colors
stroke(71, 99, 201);
strokeWeight(2);
fill(71, 99, 201, 140);
// drawing the blue quadrifolium!
beginShape();
for (var u = 0; u < nPoints; u++) {
var h = map(u, 0, nPoints, 0, TWO_PI * d2); // determine theta (the angle)
r2 = a2 * cos(k2 * h); // the equation that draws the quadrifolium
x2 = r2 * cos(h) + width / 2; // these help compute the vertex (x2, y2) using the circular identity
y2 = r2 * sin(h) + width / 2;
vertex(x2, y2);
}
endShape();
}
// the yellow center of the flower (also a smaller quadrifolium)
function flowerCenter() {
// these variables/constraints hold mouseX to the width of the canvas
// mouseX3 slows down the speed of mouseX
var mouseX3 = mouseX / 5;
var mouseMove3 = constrain(mouseX3, 0, width / 5);
// these variables/constants help determine the location of the flower via the equation and vertex
var r3;
var x3;
var y3;
// n3 and d3 help determine the k3 constant, or the number of petals on the yellow center
n3 = map(mouseMove3, 0, width, 0, 20);
d3 = 5;
// a3 determines the size of the yellow center quadrifolium
var a3 = 30;
// yellow center color
stroke(247, 196, 12);
strokeWeight(3);
fill(247, 196, 12, 50);
// drawing the yellow center quadrifolium!
beginShape();
for (var c = 0; c < nPoints; c++) {
var e = map(c, 0, nPoints, 0, TWO_PI * d3); // determine theta (the angle)
r3 = a3 * cos(k3 * e); // the equation that draws the quadrifolium
x3 = r3 * cos(e) + width / 2; // these help compute the vertex (x3, y3) using the circular identity
y3 = r3 * sin(e) + width / 2;
vertex(x3, y3);
}
endShape();
}
// the blue arrow on the bottom that indicates which way to move the mouse... toward the right!
function arrow() {
// variables for the line part of the arrow
var lineH = height - 40;
var lineS = width / 3;
var lineE = 2 * width / 3;
// variables for the arrowhead part of the arrow
var arrowH1 = lineH - 5;
var arrowHT = lineE + 10;
var arrowH2 = lineH + 5;
// the arrow!
stroke(71, 99, 201);
fill(71, 99, 201);
strokeWeight(6);
line(lineS, lineH, lineE, lineH);
triangle(lineE, arrowH1, arrowHT, lineH, lineE, arrowH2);
}I struggled initially with this project because it had been so long since I mapped parametric curves in any class, let alone in a programming class. However, as I pored through Wolfram Alpha’s libraries, the Quadrifolium, or Rose Curve, immediately jumped out at me for its simplicity and elegance. I really loved how much it looked like a flower, and I thought it was really neat how the number of petals could be manipulated based on a simple constant k before the θ in the equation:
r = a * cos(kθ)
I knew that I wanted to make my quadrifolium feel like an actual flower, so I modeled my design after the blue Chrysanthemum flower.
After I had drawn out the basic flower using multiple layers of quadrifolia, I decided to make my piece interactive by having the mouseX control the amount of petals on the flower. By doing so, I was able to make my design/curve “transform” from a basic circle into a beautiful flower!
