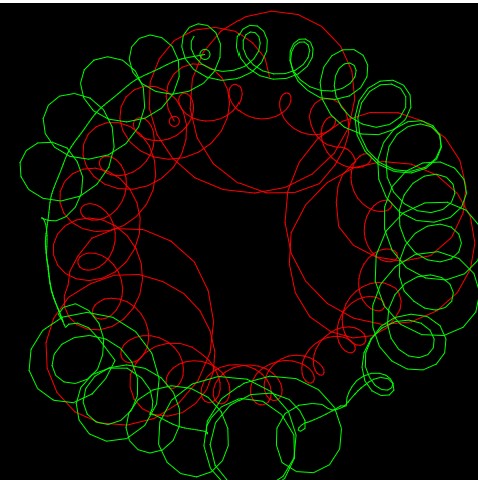
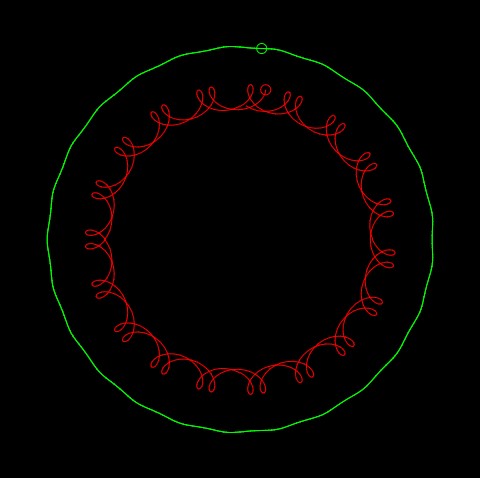
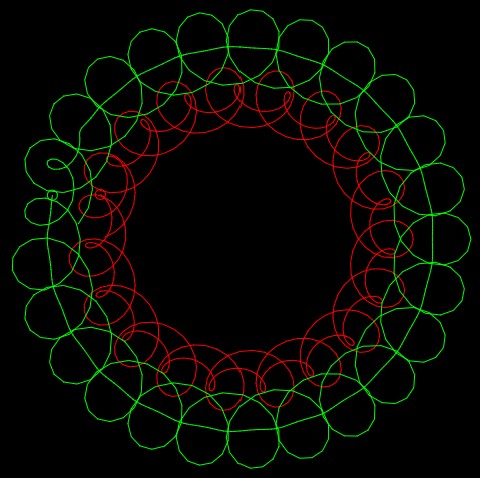
//Diana McLaughlin, dmclaugh@andrew.cmu.edu, Section A
//a code that experiments with epicycloids and hypotrochoids
var nPoints = 500;
var theta = 0;
function setup() {
createCanvas(480, 480);
}
function draw() {
var g = map(mouseX, 0, 480, 0, 160);
var b = map(mouseX, 0, 480, 75, 255);
background(0, g, b); //shades of blue
for(var y = 0; y <= 480; y += 100) { //draw the vertical yellow epicycloids
push();
translate(0, y);
Epicycloid2();
pop();
push();
translate(480, y);
Epicycloid2();
pop();
}
for (var x = 20; x <= 480; x += 100) {
push(); //top row, yellow epicycloids
translate(x, 0);
Epicycloid2();
pop();
push(); //second row, pink hypotrochoids
translate(x, 120);
Hypotrochoid1();
pop();
push(); // middle row, purple epicycloids
translate(x, 240);
Epicycloid1();
pop();
push(); //fourth row, green hypotrochoids
translate(x, 360);
Hypotrochoid2();
pop();
push(); //bottom row, yellow epicycloids
translate(x, 480);
Epicycloid2();
pop();
}
}
function Epicycloid1() { //purple epicycloid
var a = map(mouseX, 0, 480, 0, 70); //inner radius
var b = map(mouseY, 0, 480, 0, 20); //outter radius
strokeWeight(1);
stroke(255, 128, 255); //light purple
noFill();
beginShape();
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, 125, 0, TWO_PI);
x = (a+b) * cos(theta) - b * cos(((a+b)/b) * theta);
y = (a+b) * sin(theta) - b * sin(((a+b)/b) * theta);
vertex(x, y);
}
endShape();
}
function Epicycloid2() { //yellow, epicycloid, used for the border
var a = map(mouseX, 0, 480, 0, 30); //inner radius
var b = map(mouseY, 0, 480, 0, 20); //outter radius
strokeWeight(0.75);
stroke(255, 255, 0); //yellow
noFill();
beginShape();
for (var i=0; i<nPoints; i++) {
var theta = map(i, 0, 45, 0, TWO_PI);
x = (a+b) * cos(theta) - b * cos(((a+b)/b) * theta);
y = (a+b) * sin(theta) - b * sin(((a+b)/b) * theta);
vertex(x, y);
}
endShape();
}
function Hypotrochoid1() { //pink hypotrochoid
var a = map(mouseX, 0, 480, 0, 125); //outter radius
var b = map(mouseY, 0, 480, 0, 50); //inner radius
var h = map(mouseX, 0, 480, 0, 60); // tracing distance from center of inner circle
strokeWeight(1);
stroke(255, 128, 200); //pink
noFill();
beginShape();
for (var i=0; i<nPoints; i++) {
var theta = map(i, 0, 120, 0, TWO_PI);
x = (a-b) * cos(theta) + h * cos(((a-b)/b) * theta);
y = (a-b) * sin(theta) - h * sin(((a-b)/b) * theta);
vertex(x, y);
}
endShape();
}
function Hypotrochoid2() { //green hypotrochoid
var a = map(mouseX, 0, 480, 0, 100); //outter radius
var b = map(mouseY, 0, 480, 0, 40); //inner radius
var h = map(mouseY, 0, 480, 0, 60); //tracing distance from center of inner circle
strokeWeight(1);
stroke(0, 255, 0);
noFill();
beginShape();
for (var i=0; i<nPoints; i++) {
var theta = map(i, 0, 120, 0, TWO_PI);
x = (a-b) * cos(theta) + h * cos(((a-b)/b) * theta);
y = (a-b) * sin(theta) - h * sin(((a-b)/b) * theta);
vertex(x, y);
}
endShape();
}
I made this as a way to mess around with hypotrochoids and epicycloids. It took awhile to figure out the math and variables, but once I did, it was fun to play around with. The top pink row is my favorite.
![[OLD FALL 2020] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2021/09/stop-banner.png)