//Yugyeong Lee
//Section A (9:00AM)
//yugyeonl@andrew.cmu.edu
//Project-07
var nPoints = 1000;
var radiusA = 100;
var radiusB = 20;
var n = 7;
var X;
var colorG;
var colorB;
var angle;
var scaleA;
function setup() {
createCanvas(600, 600);
}
function draw() {
background(224, colorG, colorB);
stroke(255);
strokeWeight(3);
X = constrain(mouseX, 0, width);
//background color changes based on mouseX
colorG = map(X, 0, width, 200, 100);
colorB = map(X, 0, width, 150, 100);
//the shapes rotate based on mouseX
angle = map(X, 0, width, 0, 4 * TWO_PI);
//the shapes change sizes based on mouseX
scaleA = map(X, 0, width, 0, 2);
//the epicycloid (the outer shape)
push();
translate(width/2, height/2);
scale(scaleA, scaleA)
rotate(angle);
beginShape(LINES);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, 6 * TWO_PI);
var px = (radiusA + 2 * radiusB) / radiusA * ((radiusA + radiusB) * cos(theta) + radiusB * cos((radiusA + radiusB) / radiusB * theta));
var py = (radiusA + 2 * radiusB) / radiusA * ((radiusA + radiusB) * sin(theta) + radiusB * sin((radiusA + radiusB) / radiusB * theta));
vertex(px, py);
}
endShape(CLOSE)
pop();
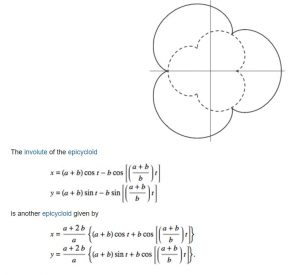
//involute of the epicycloid (the in-between shape)
push();
translate(width/2, height/2);
scale(scaleA, scaleA)
rotate(-angle);
beginShape(LINES);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, 6 * TWO_PI);
var px = (radiusA + radiusB) * cos(theta) - radiusB * cos((radiusA + radiusB) / radiusB * theta);
var py = (radiusA + radiusB) * sin(theta) - radiusB * sin((radiusA + radiusB) / radiusB * theta);
vertex(px, py);
}
endShape(CLOSE)
pop();
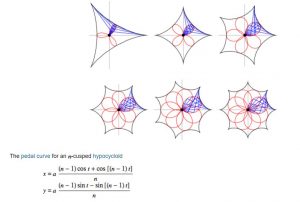
//pedal curve for an n-cusped hypocycloid (the inner shape)
push();
translate(width/2, height/2);
scale(scaleA, scaleA)
rotate(angle);
beginShape(LINES);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, 6 * TWO_PI);
var px = radiusA * (((n-1)*cos(theta) + cos((n-1)*theta)) / n)
var py = radiusA * (((n-1)*sin(theta) + sin((n-1)*theta)) / n)
vertex(px, py);
}
endShape(CLOSE)
pop();
}
I was intrigued by the idea to create flower shapes utilizing epicycloid and hypocycloid formula. I mapped the background color, size of the flower shapes, as well as its rotation to the position of mouseX. Because there are three layers of pedals, I alternated the direction of each rotation to create a more interesting shape. Also, by increasing the size of the flowers based on mouseX, the shapes appear as if it’s approaching you.
![[OLD – FALL 2016] 15-104 • COMPUTING for CREATIVE PRACTICE](wp-content/uploads/2020/08/stop-banner.png)