sketch
/* Jenni Lee
Section E
jennife5@andrew.cmu.edu
Project - 06
*/
function setup() {
createCanvas(600, 800);
}
function draw() {
var H = hour(); // brightness of the background is controlled by the hour
var bgr = 174 * (24 - H) / 24; // range of r is 42 to 216
var bgg = 166 * (24 - H) / 24; // range of g is 73 to 239
var bgb = 167 * (24 - H) / 24; // range of b is 73 to 240
background(bgr + 42, bgg + 73, bgb + 73);
// brightness of grass is controlled by color
bgr = 173 * (24 - H) / 24; // range of r is 57 to 230
bgg = 156 * (24 - H) / 24; // range of g is 81 to 237
bgb = 125 * (24 - H) / 24; // range of b is 51 to 176
noStroke();
fill (bgr + 57, bgg + 81, bgb + 51);
rect (0, 600, 600, 200);
// tail
push();
translate(400, 510);
var S = second() % 2;
if (S == 0) { // tail points to different direction depending on even or odd second number
rotate(60 / PI + PI);
} else {
rotate(120 / PI + PI);
}
noStroke();
ellipseMode(CORNER);
fill (247, 202, 201);
ellipse(0, 0, 40, 140);
pop();
// body
push();
translate(300, 570);
noStroke();
fill(229, 196, 168);
ellipse(0, 0, 250, 200);
pop();
// face
push();
translate(200, 580);
noStroke();
fill(239, 208, 172);
ellipse(0, 0, 200, 150);
pop();
//ears
push ();
noStroke();
fill(239, 208, 172); // left ear
triangle(100, 572, 102, 490, 150, 515);
fill (252, 217, 224); // left inner ear
triangle(108, 561, 110, 510, 138, 528);
//right ear
fill(239, 208, 172); // right ear
triangle(240, 512, 290, 490, 295, 560);
fill (252, 217, 224); // right inner ear
triangle(250, 521, 282, 506, 285, 553);
pop ();
// eyes. the posiiton of the eye ball is decided by
// the minutes, and it circles one round in 60 minutes
push();
translate(140, 570);
noStroke ();
fill(255, 255, 255);
// left eye
ellipse(0, 0, 36, 36);
//left eye ball
var M = minute();
angleMode(DEGREES);
fill(130, 115, 100);
ellipse(cos(M / 60 * 360 - 90) * 9, sin(M / 60 * 360 - 90) * 9, 18, 18);
// right eye
fill(255, 255, 255);
ellipse(100, 0, 36, 36);
// right eye ball
fill(130, 115, 100);
ellipse(cos(M / 60 * 360 - 90) * 9 + 100, sin(M / 60 * 360 - 90) * 9, 18, 18);
angleMode(RADIANS);
// nose
fill(130, 115, 100);
ellipse(50, 20, 10, 10);
//blush
fill(252, 217, 224);
ellipse(5, 30, 35, 10); // left blush
ellipse(95, 30, 35, 10); // right blush
pop();
// left paw
push();
translate(152, 650);
rotate(40 / PI);
strokeWeight(3);
stroke(255);
fill(239, 208, 172);
ellipse(0, 0, 80, 40);
pop();
// right paw
push();
translate(232, 650);
rotate(-40 / PI);
strokeWeight(3);
stroke(255);
fill(239, 208, 172);
ellipse(0, 0, 80, 40);
pop();
}
// The tail moves left and right every second, the eyeballs make a 360 rotation each hour,
// it moves clock wise every minute. The sky gets darker with each hour. It's the brightest
// at the beginning of the day and dark at the end of the day.
Cats are my favorite animal, so I wanted my abstract clock to be one. This project was highly enjoyable for me, as not only was it a fun challenge to design it, but it was entertaining to fully customize it to my own tastes. Seconds are indicated by the tail moving left and right each second. Minutes are indicated with the eyeballs moving clock wise every minute, completing a 360 rotation by the end of the hour. Hours/time of day is indicated through the ground and sky getting darker with each hour of the day. These two elements are very light in the morning and dark at night, similar to the sun setting.
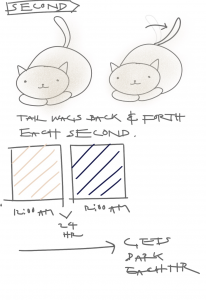
Process work ^
![[OLD FALL 2018] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)
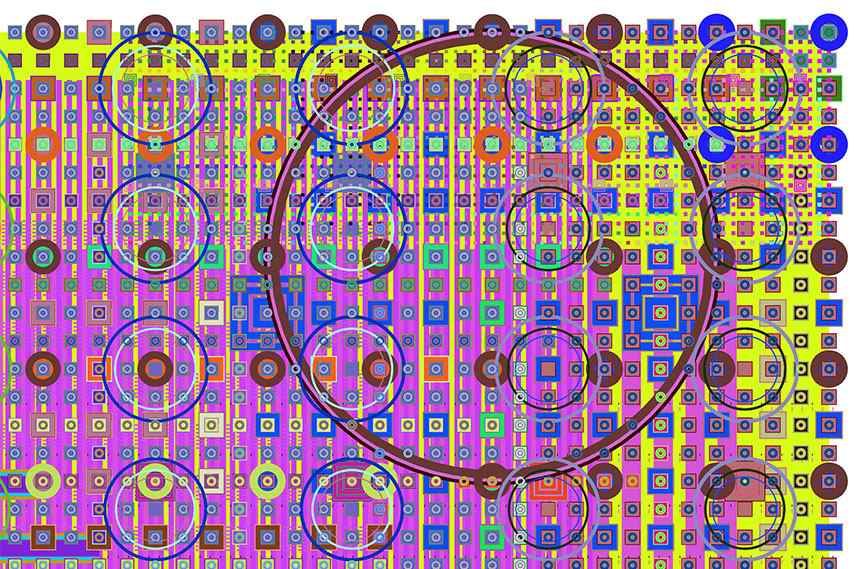 Mark Wilson’s Piece titled “e4708”
Mark Wilson’s Piece titled “e4708”
