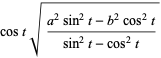Category: Section B

atreu-proj-07

/*Austin Treu
    atreu@andrew.cmu.edu
    Section B
    Project 07*/

var cX = 0, cY = 0, nPoints = 100,
    t = 0, up = 0, bot = 0, a = 0, b = 0;

function setup() {
    createCanvas(480, 480);
    frameRate(10);
}

function draw() {
    //fade the background
    background(255,255,0,20);

    //actual shape
    //shape is based upon the devil's curve
    //http://mathworld.wolfram.com/DevilsCurve.html
    fill('orange');
    push();
    //center the shape
    translate(width/2, height/2);
    //scale down to half size
    scale(0.5);

    //create the shape
    beginShape();
    //utilize mouse values for a and b
    a = mouseX;
    b = mouseY;
    for (var i = 0; i < nPoints; i++) {
        //map t around a full circle
        t = map(i, 0, nPoints, 0, TWO_PI);
        //calculate points
        up = pow(a,2)*pow(sin(t),2)-pow(b,2)*pow(cos(t),2);
        bot = pow(sin(t),2) - pow(cos(t),2);
        cX = cos(t)*(sqrt(up/bot));
        cY = sin(t)*(sqrt(up/bot));
        vertex(cX, cY);
    }
    endShape(CLOSE);
    pop();

    //accidental spiky thing
    stroke('red');
    push();
    //center the shape
    translate(width/2, height/2);
    //increase size
    scale(25);

    //create the shape
    beginShape();
    //utilize mouse values for a and b
    a = mouseX;
    b = mouseY;
    for (var i = 0; i < nPoints; i++) {
        //map t around a full circle
        t = map(i, 0, nPoints, 0, TWO_PI);
        //calculate points
        up = pow(a,2)*pow(sin(t),2)-pow(b,2)*pow(cos(t),2);
        bot = pow(sin(t),2) - pow(cos(t),2);
        //an incorrect parenthesis can change EVERYTHING!!
        cX = cos(t*(sqrt(up/bot)));
        cY = sin(t*(sqrt(up/bot)));
        vertex(cX, cY);
    }
    endShape(CLOSE);
    pop();
}

The devil’s curve is what I based this project on. I struggled through this project at the beginning, dealing with a variety of issues that prevented the program from functioning correctly. This was mainly due to two parentheses that were out of place in my math.

I mistakenly read this as cosine of the quantity of t times the square root as opposed to cosine of t times the quantity of the square root. I did the same for both x and y values. This created the red ‘starburst’ that appears in the middle of the drawing. Once I corrected this, I made a shape correctly based upon the devil’s curve but decided to leave the starburst, as it adds some interesting randomness to the image. Believe it or not, both of the things you see on screen were created with the same equation, only differing by two parentheses and scale.

sketch

//Xiaoying Meng
//xiaoyinm@andrew.cmu.edu
//Project 7
function setup(){
    createCanvas(480,480);
    frameRate(10);
}

function draw(){
    background(220);
//top curve
    push();
    translate(width/3,height/3);
    rotate(PI - mouseY/40);
    drawCurve();
    pop();
//middle curve
    push();
    translate(width/2,height/2);
    rotate(PI + mouseY/40);
    drawCurve2();
    pop();
//bottom curve
    push();
    translate(width- width/3, height- height/3);
    rotate(PI - mouseY/40);
    drawCurve3();
    pop();

   
}

//regular Crv
function drawCurve(){
    var nPoints = 200;
    var a = (mouseX-100)/3*2;
    var b = (mouseY-100)/3*2;
    fill(0);
    noStroke();
    beginShape();
    for (var i=0; i < nPoints; i++ ){
        var angle = map ( i, 0, mouseX, 0, 2*PI);
        var x = a* (1/cos(angle));
        var y = b * tan(angle);
        vertex(x,y);
    }
    endShape();
}

//wiggly Crv
function drawCurve2(){
    var nPoints = 200;
    var a = (mouseX-100)/3*2;
    var b = (mouseY-100)/3*2;
    fill(255);
    noStroke();
    beginShape();
    for (var i=0; i < nPoints; i++ ){
        var angle = map ( i, 0, mouseX, 0, 2*PI);
        var x = a* (1/cos(angle));
        var y = b * tan(angle);
        vertex(x + random(-5,5),y + random(-5,5));
    }
    endShape();
}
//dotted Crv
function drawCurve3(){
    var nPoints = 200;
    var a = (mouseX-100)/3*2;
    var b = (mouseY-100)/3*2;
    fill(150);
    noStroke();
    beginShape();
    for (var i=0; i < nPoints; i++ ){
        var angle = map ( i, 0, mouseX, 0, 2*PI);
        var x = a* (1/cos(angle));
        var y = b * tan(angle);
        ellipse(x, y, 10, 10);
    }
    endShape();
}

I chose hyperbola curves. I created three different type of representation of the curves as surfaces and lines. By rotating them to different directions, interesting abstract composition start to occur.

sketch

/*
Victoria Reiter
Section B
vreiter@andrew.cmu.edu
Project-07-Curves
*/

// initial angle of rotation for the shape
var angle = 0;

function setup() {
    // establishes canvas size
    createCanvas(480, 480);
}

function draw() {
    // sets background color
    // the same one as from my ptoject 3... I really like it:)
    // the opacity gives it a cool fading effect!
    background('rgba(255,187,203,0.05)');
    // C's get DEGREES
    angleMode(DEGREES);
    // declares variables that will be used in the mathy-math later on
    var x;
    var y;
    var radius1;
    var radius2;
    var ratio1;
    var ratio2;
    // center x and center y points
    var cx = width / 2;
    var cy = height / 2;
    // color of shape's line will change as mouse moves from right to left
    var strokeColor = map(mouseX, 0, width, 0, 255);
    // color of shape's fill will change as mouse moves from right to left
    var fillColor = map(mouseX, 0, width, 255, 0);
    // makes that angle of rotation will change as mouse moves up and down
    var increment = map(mouseY, 0, height, 0, 7);

    beginShape();
    stroke(strokeColor);
    fill(fillColor);
    push();
    // draws at center of canvas
    translate(cx, cy);
    rotate(angle);
    // math *bows*
    for (var theta = 0; theta < 360; theta +=1) {
        radius1 = 70;
        radius2 = 30;
        ratio1 = map(mouseX, 0, width, 10, 200);
        x = (radius1 * cos(theta) + radius2 * cos(theta * ratio1));
        y = (radius1 * sin(theta) + radius2 * cos(theta * ratio1));
        vertex(x, y);
    }
    // makes the shape rotate
    angle = angle + increment;
    endShape(CLOSE);
    pop();
}

So doing this project, I struggled a bit because, uh, I haven’t had to use cos or sin since highschool….
Anyway. I got inspiration from Spirographs, since I think they’re cool and vintage-y and nostalgic and remind me of being little and stories my parents have told me. But how does one draw a Spirograph??? I took to the internet to find out. I found many very unhelpful resources, and one most-helpful one, here. It listed the equations x = cx + radius1 × cos(θ) + radius2 × cos(θ) and y = cy + radius1 × sin(θ) + radius2 × cos(θ), which I used to design my curve.

I have interactive elements for the shape fill, shape color, density(?) of curves comprising the shape, and speed of rotation.

And I made the background pretty pink with the opacity toyed with for a cool effect, stolen from my own Project 3 assignment because I like this effect so much.

Very trippy, this project. Quite trippy.

sketch

//Name: Alessandra Fleck 
//Class Section : B
//Email: afleck@andrew.cmu.edu
//Project-07


var Points = 500; //more points makes smoother curves
var Epitrochoid = 0; 

var x;
var y;



function setup() {
    createCanvas(480, 480);
    frameRate(40); //more frames = clearer motion
}

function draw() {
    background(0); // set background to black
    // draw the Epitrochoid

    push();
    translate(300, height / 2); //locate at upper left corner
    drawEpitrochoidCurve_01();
    //move second curve to lower right corner
    translate(width / 10, height/10);
    drawEpitrochoidCurve_02();
    //move second curve to lower right corner
    translate(width / 60, height/60);
    drawEpitrochoidCurve_03();
    pop();
}


function drawEpitrochoidCurve_01() { // for the curve on the top left corner
    
    
    var a =  40.0;
    var b = a / 0.2;
    var h = constrain(mouseY / 10.0, 0, b);
    var t;
    var mX = mouseX / 100.0; // mouse move over moves shape slower as value is larger
    var r = map(mouseX,0,width/0.8,0,1); //pulsing movement
    
    beginShape();
    fill(40,41,35);
    for (var i = 0; i < Points; i++) {

        stroke('red'); //add red to vibration lines
        strokeWeight(3);
        vertex(x, y);
        var t = map(i, 0, Points, 0, TWO_PI*3); // mess with curves within shapes

        //Parametric equations for Epitrochoid Curve
        x = r* ((a + b) * cos(t) - h * cos((t * (a + b) / b) + mX));
        y = r* ((a + b) * sin(t) - h * sin((t * (a + b) / b) + mX));
        
    }
    endShape(CLOSE);
    
}

function drawEpitrochoidCurve_02() { //for the curve on the bottom corner
    
    
    
    var a =  55.0;
    var b = a / 0.25; //degree of displacement
    var h = constrain(mouseY / 20.0, 0, b);
    var t;
    var mX = mouseX / 50.0;
    
    
    beginShape();
    fill(0);
    for (var i = 0; i < Points; i++) {
        stroke('red'); //add red to vibration lines
        strokeWeight(3);
        vertex(x+200, y+200);//set center point for the epitrochoid
        var t = map(i, 0, Points, 0, TWO_PI*3); // mess with curves within shapes
        
        //Parametric equations for Epitrochoid Curve

        x = (a + b) * cos(t) - h * cos((t * (a + b) / b) + mX);
        y = (a + b) * sin(t) - h * sin((t * (a + b) / b) + mX);
        
    }
    endShape(CLOSE);
    
}

function drawEpitrochoidCurve_03() { //for the curve on the bottom corner
    
    //light white line curves
    
    var a =  40.0;
    var b = a / 0.25; //degree of displacement
    var h = constrain(mouseY / 10.0, 0, b);
    var t;
    var mX = mouseX / 50.0;
    
    
    beginShape();
    fill(40,41,35);
    for (var i = 0; i < Points; i++) {
        stroke(255); //add red to vibration lines
        strokeWeight(1);
        vertex(x+200, y+200);
        var t = map(i, 0, Points, 0, TWO_PI*3); // mess with curves within shapes
        
        //Parametric equations for Epitrochoid Curve

        x = (a + b) * cos(t) - h * cos(mX + ((a + b) / b) + mX);
        y = (a + b) * sin(t) - h * sin(mX + ((a + b) / b) + mX);
        
    }
    endShape(CLOSE);
    
}

//http://mathworld.wolfram.com/Epitrochoid.html

For this project I just wanted to play with using the “b” variable in the parametric equation for an epitrochoid and using that variable as the axis for the degree of change in the movement. I did struggle a bit with the vertex parameter so if I continue this project that is what I would look to refine.

sketch,js

/* Arden Wolf
Section B
ardenw@andrew.cmu.edu
Project 07
*/


var nPoints = 20;
var radius = 50;
var separation = 125;

function setup() {
    createCanvas(480, 480);
    frameRate(10);
}

function draw() {
    background(0);
    noStroke();
    //magenta
    fill (50);
    ellipse(125,120,100,100);
    fill (80);
    ellipse(125,120,80,80);
    fill (100);
    ellipse(125,120,50,50);
    fill (120);
    ellipse(125,120,30,30);


    //yellow
    fill (50);
    ellipse(377,240,100,100);
    fill (80);
    ellipse(377,240,80,80);
    fill (100);
    ellipse(377,240,50,50);
    fill (120);
    ellipse(377,240,30,30);


    //calls light beam
    LightBeam(); 
    //calls wiggle
     wiggle();
    //call square
     square();



}

function LightBeam() {
  for(var h = 0; h < 100; h++) //allows for thicker lines
    {
        //yellow
         push();
        translate(3 * separation, height / 2);
        for (var i = 0; i < nPoints; i++) {
        var theta = map(i, mouseX, nPoints, mouseY, TWO_PI);
        var px = radius * cos(theta);
        var py = radius * sin(theta);
        stroke (255,255,0);
        line(-375, 238, px, py);
        }
        pop();

         push();
        translate(3 * separation, height / 2);
        for (var i = 0; i < nPoints; i++) {
        var theta = map(i, mouseX, nPoints, mouseY, TWO_PI);
        var px = radius * cos(theta);
        var py = radius * sin(theta);
        stroke (255,255,0);
        line(0, 238, px, py);
        }
        pop();



        //magenta
         push();
        translate( separation, height / 4);
        for (var i = 0; i < nPoints; i++) {
        var theta = map(i, mouseX, nPoints, mouseY, TWO_PI);
        var px = radius * cos(theta);
        var py = radius * sin(theta);
        stroke (255,0,255);
        line(360, 365, px, py);
        }
        pop();

         push();
        translate( separation, height / 4);
        for (var i = 0; i < nPoints; i++) {
        var theta = map(i, mouseX, nPoints, mouseY, TWO_PI);
        var px = radius * cos(theta);
        var py = radius * sin(theta);
        stroke (255,0,255);
        line(360, 0, px, py);
        }
        pop();
    }

}
function wiggle(){
    stroke(4);

    //first
    fill(255,165,0);
    push();

    translate(separation, height/1.7);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var theta = map(i, mouseX, nPoints, mouseY, TWO_PI);
        var px = radius * cos(theta);
        var py = radius * sin(theta);
        vertex(px + random(-5, 5), py + random(-5, 5));
    }
    endShape(CLOSE);
    pop();

    //second
    fill(255,100,10);
    push();
    translate(separation, height/1.7);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var theta = map(i, mouseX, nPoints, mouseY, TWO_PI);
        var px = radius * cos(theta)/2;
        var py = radius * sin(theta)/2;
        vertex(px + random(-5, 5), py + random(-5, 5));
    }
    endShape(CLOSE);
    pop();

}

function square(){
//first
    fill(255,100,10);
    push();
    translate(2*separation+40, height/1.18);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var theta = map(i, mouseX, nPoints, mouseY, TWO_PI);
        var px = radius * cos(theta);
        var py = radius * sin(theta);
        vertex(px + random(-5, 5), py + random(-5, 5));
    }
    endShape(CLOSE);
    pop();

//second
    fill(255,165,0);
      push();
    translate(2*separation+40, height/1.18);
   beginShape();
    for (var i = 0; i < nPoints; i++) {
        var theta = map(i, mouseX, nPoints, mouseY, TWO_PI);
        var px = radius * cos(theta)/2;
        var py = radius * sin(theta)/2;
        vertex(px + random(-5, 5), py + random(-5, 5));
    }
    endShape(CLOSE);
    pop();
}

I was inspired by commits and stars in space and used the equations, mouseX and mouseY to make it interactive.

sketch

//Yinjie Tian
//Section B
//yinjiet@andrew.cmu.edu
//Assignment-07-A
function setup() {
    createCanvas(480, 480);
    frameRate(10);
}

function draw() {
    background(0);
    noFill();
    stroke(255, random(150,255), 255)
    var nPoints = 20;
    var radius = width / 2 - mouseX;
    var radius2 = width / 2 - mouseX * random(0.4, 0.9)
    var radius3 = width / 2 - mouseX * random(0.4, 0.9)
    var radius4 = width / 2 - mouseX * random(0.4, 0.9)
    var radius5 = width / 2 - mouseX * random(0.4, 0.9)
    var radius6 = width / 2 - mouseX * random(0.4, 0.9)
   
    
    
    // draw the circle as a wiggly circle
    push();
    
    translate(width / 2, height / 2);
    beginShape();

    for (var a = 0; a < nPoints; a++) { //circle 1
        var theta = map(a, 0, nPoints, 0, TWO_PI);
        var px = radius * cos(theta);
        var py = radius * sin(theta);
        vertex(px + random(-5, 5), py + random(-5, 5));
    }
        noFill();
        stroke(random(150,255), 255, 255)
     for (var b = 0; b < nPoints; b++) {    //circle 2
        var theta = map(b, 0, nPoints, 0, TWO_PI);
        var px = radius2 * cos(theta);
        var py = radius2 * sin(theta);
        vertex(px + random(-5, 5), py + random(-5, 5));
    }
    noFill();
        stroke(random(150,255), random(150,255), random(150,255))
     for (var c = 0; c < nPoints; c++) {    //circle 3
        var theta = map(c, 0, nPoints, 0, TWO_PI);
        var px = radius3 * cos(theta);
        var py = radius3 * sin(theta);
        vertex(px + random(-5, 5), py + random(-5, 5));
    }
     for (var d = 0; d < nPoints; d++) {    //circle 4
        var theta = map(d, 0, nPoints, 0, TWO_PI);
        var px = radius4 * cos(theta);
        var py = radius4 * sin(theta);
        vertex(px + random(-5, 5), py + random(-5, 5));
    }
        noFill();
        stroke(random(150,255), 255, 255)
     for (var e = 0; e < nPoints; e++) {    //circle 5
        var theta = map(e, 0, nPoints, 0, TWO_PI);
        var px = radius5 * cos(theta);
        var py = radius5 * sin(theta);
        vertex(px + random(-5, 5), py + random(-5, 5));
    }
    noFill();
        stroke(random(150,255), random(150,255), random(150,255))
     for (var f = 0; f < nPoints; f++) {    //circle 6
        var theta = map(f, 0, nPoints, 0, TWO_PI);
        var px = radius6 * cos(theta);
        var py = radius6 * sin(theta);
        vertex(px + random(-5, 5), py + random(-5, 5));
    }
    endShape(CLOSE);
    pop();
    
    
    
}

For this project, I first choose the ellipse as the base geometry. Then I use vertex to make each of the ellipse to wiggle. The radius for the ellipse are selected randomly based on the mouseX position. Colors for the curves are also selected randomly.