Category: Section B

sketch

/*
Romi Jin
Section B
rsjin@andrew.cmu.edu
Project-07
*/

var x;

function setup() {
    createCanvas(480, 480);
    
}

function draw() {
    
    background(174, 198, 207);

    x = constrain(mouseX, 0, width);
    y = constrain(mouseY, 0, height);
    
    //three intersecting hypotrochoids

    push();
    translate(width/2, height/2);
    drawHypotrochoid();
    pop();

    push();
    translate(width/3, height/3);
    drawHypotrochoid();
    pop();

    push();
    translate(width-width/3, height-width/3);
    drawHypotrochoid();
    pop();

}

function drawHypotrochoid() {

    //link: http://mathworld.wolfram.com/Hypotrochoid.html
    //roulette by drawing along two cirles (radius a and b below)

    for (var i = 0; i < TWO_PI; i ++) { 

        a = map(y, 0, height, 100, 200); 
        b = map(x, 0, width, 0, 75); 
        h = 100;

        x = (a - b) * cos(i) + h*cos(((a-b)/b) * i);
        y = (a - b) * sin(i) - h*sin(((a-b)/b) * i);

        noFill();
        stroke(255);
        strokeWeight(1);
        ellipse(0, 0, x, y);

    }

}

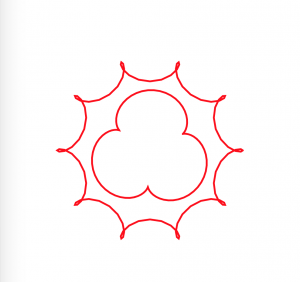
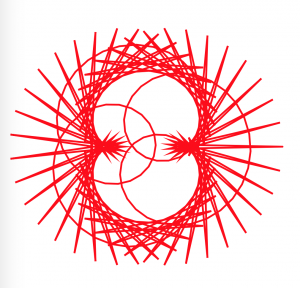
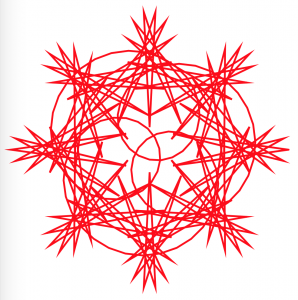
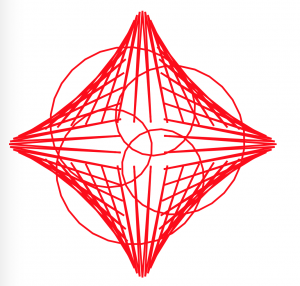
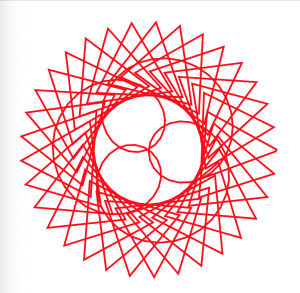
For this project, I chose the shape hypotrochoid and drew it three times to create three intersecting hypotrochoids. The parameters are the mouse X and mouse Y position, and the mouse X changes one ellipse’s radius while mouse Y changes the other. It is intriguing to watch the three intersect as they create even more curves together.

sketch

// Shirley Chen
// Section B
// junfanc@andrew.cmu.edu
// Project-07


function setup(){
	createCanvas(480, 480);
	angleMode(DEGREES);
}

function draw(){
	background(242, 186, 176);
	curveA();
	curveB();
}

function curveA(){
//Create the Fixed-Position Astroid Curve
    noFill();
    beginShape();
    var col = mouseX * 0.3;
    stroke(221, 127, col);
    translate(100, 200);
    for (var i = 0; i < mouseX/2; i ++){ 
//The Number of Curves Will Change According to MouseX
        LimitedMouseX = constrain(mouseX, 0, width);
        var cons = map(LimitedMouseX, 0, width, 10, 100); 
//The Angle Will Change According to MouseX
        var theAngle = map(i, 0, mouseX, 20, 360);
        var x = 2 * cons * cos(theAngle) + cons * cos(2 * theAngle);
        var y = 2 * cons * sin(theAngle) - cons * sin(2 * theAngle);
        vertex(x, y);
    endShape();
//Rotate The Curves According to MouseX
    rotate(mouseX); 
    }
}


function curveB(){
//Create the Moving Astroid Curve
    noFill();
    beginShape();
    var col = mouseY * 0.5;
    stroke(col, col, 110);
    translate(150, 200);
    for (var i = 0; i < mouseY*0.7; i ++){ 
//The Number of Curves Will Change According to MouseY
        LimitedMouseY = constrain(mouseY, 0, height);
        var cons = map(LimitedMouseY, 0, width, 10, 100); 
//The Angle Will Change According to MouseY
        var theAngle = map(i, 0, mouseY, 20, 360);
        var x = 2 * cons * cos(theAngle) + cons * cos(2 * theAngle);
        var y = 2 * cons * sin(theAngle) - cons * sin(2 * theAngle);
        vertex(x, y);
    endShape();
//Rotate The Entire Astroid Curve According to MouseY
    rotate(mouseY); 
    }
}

In This Project, I created a set of stable astroid curve at a fixed position and a movable set of astroid curve that keeps rotating around a center point. For the fixed set of astroid curves, the number of curves and the angle are based on the position of mouse X; for the movable set of curves, the number of curves and the angle are based on the position of mouse Y. Therefore, I used map and constrain command to limit my X and Y positions. Moreover, the colors are also changed according to the mouse X and Y. For the fixed-position set of curves, the curves inside the set is rotating according to the mouse X. For the movable set of curves, the curves inside the set and the set itself are both rotating according to the position of Y.

sketch

/*
Veronica Wang
Section B
yiruiw@andrew.cmu.edu
Project 07
*/

var nPoints = 100;


function setup() {
    createCanvas(480, 480);
    frameRate(10);
}


function draw() {
    background(255);
   
    // draw the curves
    push();
    translate(width / 2, height / 2);
    drawEpitrochoidCurve();
    drawHypotrocoidCurve();
    pop();


}

//--------------------------------------------------
function drawEpitrochoidCurve() {
    // Epicycloid:
    // http://mathworld.wolfram.com/Epicycloid.html
    
    var x;
    var y;
    
    var a = 60.0;
    var b = a / 3.0;
    var h = constrain(mouseY / 2, 0, width / 5);
    var ph = mouseX / 50.0;
    
    noFill();
    stroke('red');
    strokeWeight(3);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        
        x = (a + b) * cos(t) - h * cos(ph + t * (a + b) / b);
        y = (a + b) * sin(t) - h * sin(ph + t * (a + b) / b);
        vertex(x, y);
    }
    endShape(CLOSE);  
}

function drawHypotrocoidCurve(){
    //Hypocycloid
    //http://mathworld.wolfram.com/Hypotrochoid.html
    var x;
    var y;

    var a1 = 200;
    var b1 = a1 / 3.0;
    var h1 = constrain(mouseY / 2, 0, width / 5);
    var ph1 = mouseX / 10.0;

    noFill();
    stroke('red');
    strokeWeight(3);

    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        
        x = (a1 - b1) * cos(t) + h1 * cos((ph1 + (a1 - b1) / b1) * t);
        y = (a1 - b1) * sin(t) - h1 * sin((ph1 + (a1 - b1) / b1) * t);
        vertex(x, y);
    };
    endShape(CLOSE);
}

In this project, I used both the hypotrochoid and epitrochoid curves to create interesting compositions. I played around with the amplitude, divisions, diameters, etc of the curve functions. I think it’s interesting how sometimes the animation can sort of explain how the hypotrochoids were generated-when you can see a straight line rotating at the ‘beginning’ point.

sketch-131

function setup() {
  createCanvas(400, 400);
}

function draw() {
  background(0);
  fill(186, 85, 211, 100);
  strokeWeight(.25);
  stroke('black');
  drawHypocycloid();
}

function drawHypocycloid() {
  var x;
  var y;
  var theta;
  var nPoints = map(mouseY, 0, height, 50, 100);
    
  beginShape();

  for (var i = 0; i < nPoints; i++) {
    
    push();

    var a = map(mouseX, 0, width, 0, 50);
    var n = map(mouseY, 0, height, 0, 200);
    var d = map(mouseX, 0, width, 10, 20);

    theta = i;

    x = ((a / n) * (n - 1)*cos(theta)) - (d*(cos((n-1)*theta)));
    y = ((a / n) * (n - 1)*sin(theta)) + (d*(sin((n-1)*theta)));

    vertex(x + width/2, y + height/2);
    pop();
  }

  endShape(CLOSE);

  beginShape();

  for (var i = 0; i < nPoints; i++) {

    push();

    var a = map(mouseX, 0, width, 100, 0);
    var n = map(mouseY, 0, height, 400, 0);
    var d = map(mouseX, 0, width, 10, 20);

    theta = i;

    x = ((a / n) * (n - 1)*cos(theta)) - (d*(cos((n-1)*theta)));
    y = ((a / n) * (n - 1)*sin(theta)) + (d*(sin((n-1)*theta)));
    vertex(x + width/2, y + height/2);

    pop();
  }
  endShape(CLOSE);

  beginShape();

  for (var i = 0; i < nPoints; i++) {
    
    push();

    var a = map(mouseX, 0, width, 0, 100);
    var n = map(mouseY, 0, height, 0, 400);
    var d = map(mouseX, 0, width, 10, 20);

    theta = i;

    x = ((a / n) * (n - 1)*cos(theta)) - (d*(cos((n-1)*theta)));
    y = ((a / n) * (n - 1)*sin(theta)) + (d*(sin((n-1)*theta)));

    vertex(x + width/2, y + height/2);
    pop();
  }

  endShape(CLOSE);
}

For this project, I focused on the hypocycloid curve. 

http://mathworld.wolfram.com/Hypocycloid.html

The hypocycloid is based on the idea of a circle, of smaller radius, rolling along the inside of a larger circle, with a point drawing it’s curve throughout the rotation. For my project I first began exploring variations based on the number of points and how adding different variables to the equation could influence it’s shape.

I then began playing around graphically, adding in 3 layers of these hypocycloid curves, and filling in the curves, to almost recreate a flower in bloom. It’s quite interesting to me how these circles are proportional to one another but act quite differently at certain points in the canvas.

I added in the d variable, which creates even more variation, based on the Astroid curve, http://mathworld.wolfram.com/Astroid.html, which is a type of hypocycloid.

sketch

var nPoints = 200;  //set number of vertex points for trifolium shape

function setup() {
    createCanvas(400, 400);
}

function draw() {
    background(255);
    noStroke();
   
    //draw center trifolium
    push();
    translate(width/2, height/2);
    fill("blue");
    drawTrifolium();
    pop();

    //draw upper left trifolium
    fill("violet");
    drawTrifolium();

    //draw upper right trifolium
    push();
    translate(width, 0);
    fill("violet");
    drawTrifolium();
    pop();

    //draw lower left trifolium
    push();
    translate(0, height);
    fill("violet");
    drawTrifolium();
    pop();

    //draw lower right trifolium
    push();
    translate(width, height);
    fill("violet");
    drawTrifolium();
    pop();
}

//draw Trifolium shape based on mouseX, mouseY
function drawTrifolium() {

    var x;
    var y;
    var r;
    var theta;

    var a = mouseY; //mouseY governs size of trifolium
    var petals = map(mouseX, 0, width, 2, 45); //mouseX governs number of petals
    var petalsInt = round(petals); //rounds petals to nearest integer (no partial petals)

    //create base trifolium shape using equation from Mathworld
    beginShape(); 
    for (var i = 0; i < nPoints; i++) {
        theta = map(i, 0, nPoints, 0, TWO_PI);
        r = -a * cos(petalsInt * theta);
        x = r * cos(theta);
        y = r * sin(theta);
        vertex(x,y);
    }
    endShape(CLOSE);
}

I found the trifolium curve on Mathworld and decided to see what it could do.

I discovered that changing one number in the equation would cause more “petals” to appear on the trifolium (making it not exactly a “tri”folium anymore, but it looks great), and set this to mouseX. Testing another variable, I found it governed the size of the trifolium shape, so I set this to correspond to mouseY.

To make things more interesting, I added four more trifoliums in the corners of the canvas (so only a corner of each was visible). I started with each one a different color:

…but decided I preferred the patterns that emerged when all 4 corner shapes were the same color, creating a more ambiguous web rather than 4 distinct shapes.