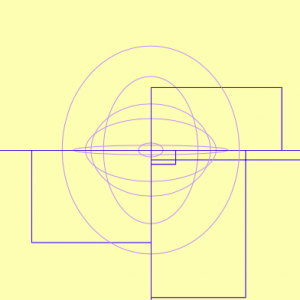
sketch
function setup() {
createCanvas(480, 480);
frameRate(10);
}
function draw () {
background(0)
noFill()
stroke(255)
var nPoints = 20;
var radius = 50;
var separation = 125;
var R1 = mouseX/2
var R2 = mouseY/2
//the color of the pattern changes slowly from bluee to red as the mouse moves along the diagnal of canvas
//the first set of rectangle loop
stroke(mouseX, 10, 10)
push();
translate(2*separation, height / 2);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var px = R1 * cos(theta);
var py = R2 * sin(theta);
rect(px - 5, py - 5, 10, 10);
}
pop();
//the second set of rectangle loop
stroke(mouseX, 30, 30)
push();
translate(2*separation, height / 2);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var px = R1 * cos(theta);
var py = R2 * sin(theta);
rect(px - 10, py - 10, 20, 20);
}
pop();
//the third set of rectangle loop
stroke(mouseX, 50, 50)
push();
translate(2*separation, height / 2);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var px = R1 * cos(theta);
var py = R2 * sin(theta);
rect(px - 15, py - 15, 30, 30);
}
pop();
//the fourth set of rectangle loop
stroke(mouseX, 70, 70)
push();
translate(2*separation, height / 2);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var px = R1 * cos(theta);
var py = R2 * sin(theta);
rect(px - 30, py - 30, 60, 60);
}
pop();
//the fifth set of rectangle loop
stroke(mouseX, 90, 90)
push();
translate(2*separation, height / 2);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var px = R1 * cos(theta);
var py = R2 * sin(theta);
rect(px - 50, py - 50, 100, 100);
}
pop();
//the sixth set of rectangle loop
stroke(mouseX, 110, 110)
push();
translate(2*separation, height / 2);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var px = R1 * cos(theta);
var py = R2 * sin(theta);
rect(px - 90, py - 90, 180, 180);
}
pop();
//the seventh set of rectangle loop
stroke(mouseX, 140, 140)
push();
translate(2*separation, height / 2);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var px = R1 * cos(theta);
var py = R2 * sin(theta);
rect(px - 95, py - 95, 190, 190);
}
pop();
//the eighth set of rectangle loop
stroke(mouseX, 170, 170)
push();
translate(2*separation, height / 2);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var px = R1 * cos(theta);
var py = R2 * sin(theta);
rect(px - 100, py - 100, 200, 200);
}
pop();
//the nineth set of rectangle loop
stroke(mouseX, 220, 220)
push();
translate(2*separation, height / 2);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints, 0, TWO_PI);
var px = R1 * cos(theta);
var py = R2 * sin(theta);
rect(px - 105, py - 105, 210, 210);
}
pop();
}
In this project, I wanna design a floral pattern that can change colors using repeating geometries. The flower’s color changes to blue to read as the mouse moves diagonally on the canvas. The change of color also represents blossom.
![[OLD FALL 2018] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)