Curves

I decided to chose the Devil’s Curve for my project, mostly because I liked the way it looked. It was very hard at first because I have not been in a math class in years, to figure out what each part of my equations did. At first I had a problem where my signs were wrong and only had the crunode show up.

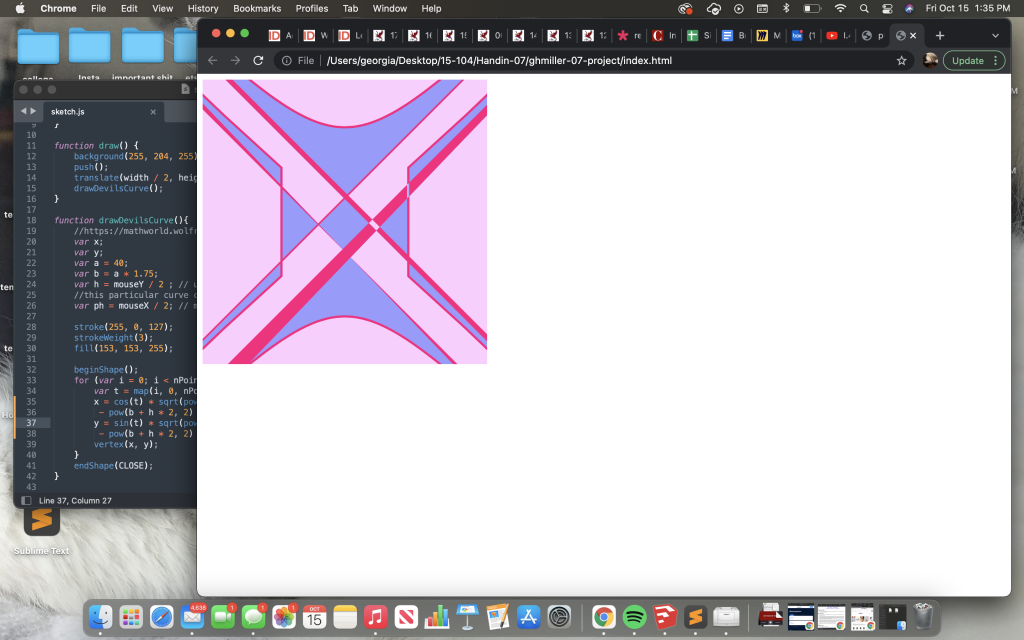
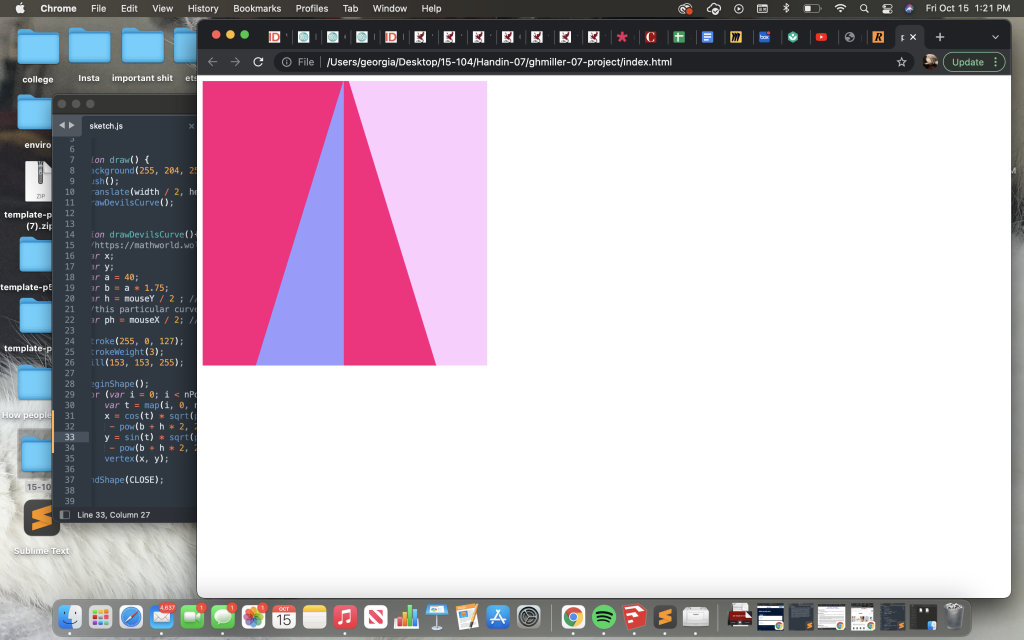
I got stuck for a bit, but the project seemed simpler than I thought at first. To better understand and to play around with my curve to figure out how I should have it move, I was able to find an example of the curve and move it’s a and b points on desmos. One thing I had already accidentally realized was that if a and b were equal they would make a circle and if a/b was more or less than one rotated the crunode. I thought these properties were interesting so I wanted to attach my b value and a values to movements so that they would be able to both equal each other and be more than and less than. Doing this also allowed my curve to grow and shrink.

The code works so so that mouseX and Y control a and b. They do the same thing to the numbers but depending on the position of the mouse on the page it controls rotation of the crunode and size.

file

//Georgia Miller
//Section D
//15-104

nPoints = 400;
function setup() {
    createCanvas(400, 400);
    frameRate(10);
}

function draw() {
    background(255, 204, 255);
    push();
    translate(width / 2, height / 2);
    drawDevilsCurve();
}

function drawDevilsCurve(){
    //https://mathworld.wolfram.com/DevilsCurve.html
    var x;
    var y;
    var a = 40;
    var b = a * 1.75;
    var h = mouseY / 2 ; // up and down to change crunode
    //this particular curve changes orientation based on if a/b is bigger or larger than 1
    var ph = mouseX / 2; // move mouse to right to grow

    stroke(255, 0, 127);
    strokeWeight(3);
    fill(153, 153, 255);

    beginShape();
    for (var i = 0; i < nPoints; i++){
        var t = map(i, 0, nPoints, 0, TWO_PI); //t = theta
        x = cos(t) * sqrt((pow(a + ph, 2) * pow(sin(t), 2) 
         - pow(b + h * 2, 2) * pow(cos(t), 2)) / (pow(sin(t), 2) - pow(cos(t), 2)));
        y = sin(t) * sqrt((pow(a + ph, 2) * pow(sin(t), 2)
         - pow(b + h * 2, 2) * pow(cos(t), 2)) / (pow(sin(t), 2) - pow(cos(t), 2)));
        vertex(x, y);
    }
    endShape(CLOSE);
}