sketchDownload
var bgR;
var bgG;
var bgB;
var x;
var y;
function setup() {
createCanvas(480, 480);
frameRate(10);
}
function draw() {
bgR = map(-mouseY, 0, height, 50, 100); //select random background colors
bgG = map(-mouseX, 0, width, 50, 200);
bgB = map(-mouseY, 0, height, 0, 100);
background(bgR, bgG, bgB);
translate(220, 220);
for (var c = 1; c < 5; c ++){ //draw the curve
for (var d = 1; d < 5; d ++){
push();
translate(c * 10, d * 10);
drawEpicycloidPedalCurve(); //reference to link -- https://mathworld.wolfram.com/EpicycloidPedalCurve.html
pop();
}
}
}
function drawEpicycloidPedalCurve() {
var a = map(mouseX, 0, width, 15, 100); //parameter of the curve moves with the mouse
var b = map(mouseY, 0, height, 15, 50);
noFill();
stroke(mouseX, mouseY, 180);
strokeWeight(0.8);
push();
beginShape(); //draw the curve
for (var i = 0; i <= 600; i ++) {
var theta = map(i, 0, 100, 0, PI);
x = (a+b)*cos(theta) - b*cos(((a+b)*theta)/b); //epicycloids are given by the parametric equations
y = (a+b)*sin(theta) - b*sin(((a+b)*theta)/b);
vertex(x, y);
}
endShape();
pop();
}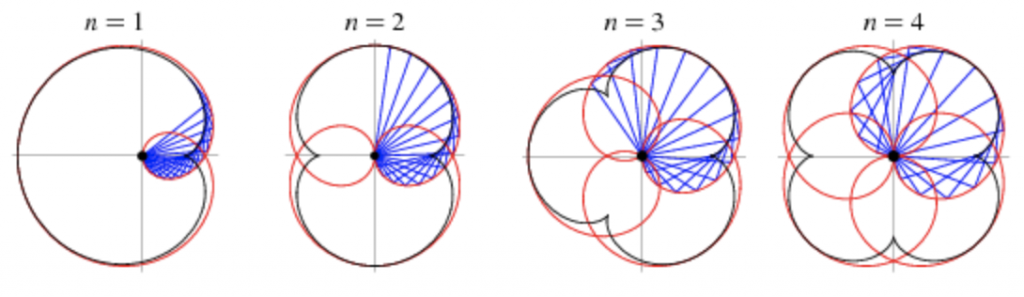
For this project, I wanted to iterate a flower-like shape using parameter equations so I decided to draw Epicycloid Pedal Curve as the composition. I played with mouseX and mouseY as well as random RGB colors across the canvas so the user has the freedom to explore with unique variations of epicycloid pedal curve patterns.
![[OLD SEMESTER] 15-104 • Introduction to Computing for Creative Practice](wp-content/uploads/2023/09/stop-banner.png)





