sketch
//Sihan Dong
//sihand@andrew.cmu.edu
//Section B
//Project 03 snowflakes: this program is a interactive art
function setup() {
createCanvas(640, 480);
}
function draw() {
background(13,33,61);
noStroke();
fill(255);
//leftmost snowflake
//the diameter of the center circle is set between 20 and 70
//three layers circulate at the same speed,
//while the second layer is the satellie of the first, and the thrid the second
var size1 = 50 * noise(0.005*frameCount + 60);
var circle1 = constrain(size1, 20,70);
//defining the center circle
ellipse(width/2-150, height/2, circle1, circle1);
//if cursor is placed within the circle snowflake appears
if (dist(mouseX, mouseY, width/2-150, height/2) < circle1/2) {
var ang1 = TWO_PI * 0.005*frameCount + 20;
var ang3 = TWO_PI * 0.005*frameCount + 30;
for (var i = 0; i < 8; i++) {
push();
translate(width/2-150, height/2);
rotate(ang1 + TWO_PI * i / 8);
translate(100, 0);
ellipse(0, 0, 20, 20);
if (frameCount >300) {
push();
rotate(ang1 + TWO_PI * 1 / 6);
ellipse(50, 0, 10, 10);
if (frameCount > 600) {
push();
translate(80,0);
rotate(ang1 + TWO_PI * 1 / 6);
ellipse(0, 0, 10, 10);
rotate(ang3);
pop();
}
pop();
}
pop();
}
}
//middle snowflake
//defining the center circle
var size2 = 80 * noise(0.005*frameCount + 60);
var circle2 = constrain(size2, 30,80);
ellipse(width/2, height/2, circle2, circle2);
//varying distance between layers
var rx = 200 * noise(0.005*frameCount + 40);
var tx = 150 * noise(0.005*frameCount + 50);
var circle3 = constrain (size2, 10, 20);
if (dist(mouseX, mouseY, width/2, height/2) < circle1/2) {
var ang1 = TWO_PI * 0.005*frameCount + 20;
var ang2 = TWO_PI * 0.0005*frameCount + 10;
var ang3 = TWO_PI * 0.005*frameCount + 30;
for (var i = 0; i < 6; i++) {
push();
translate(width/2, height/2);
rotate(ang1 + TWO_PI * i / 6);
translate(tx, 0);
ellipse(0, 0, circle3, circle3);
rotate(ang3);
if (frameCount >200) {
for (var j = 0; j < 3; j++) {
push();
rotate(ang2 + TWO_PI * j / 15);
//three satellites will go around the second layer closely
incre = 10;
ellipse(rx, 0, 9, 9);
pop();
}
}
pop();
}
}
//rightmost snowflake
var size1 = 100 * noise(0.005*frameCount + 60);
var circle1 = constrain(size1, 30,130);
//the diameter of the center circle is set between 30 and 130
ellipse(width/2+150, height/2, circle1, circle1);
//defining the center circle
var ux = 150 * noise(0.005*frameCount + 30);
if (dist(mouseX, mouseY, width/2+150, height/2) < circle1/2){
for (var i = 0; i < 8; i++) {
push();
translate(width/2+150, height/2);
rotate(TWO_PI * i / 8);
//rotate(ang1 + TWO_PI * i / 8);
translate(ux*1.25, 0);
ellipse(0, 0, 20, 20);
if (frameCount >200) {
for (var j = 0; j < 6; j++){
push();
rotate(TWO_PI * j / 6);
translate(0.5*ux,0);
ellipse(0, 0, 10, 10);
if (frameCount > 400) {
for (var j2 = 0; j2 < 6; j2++){
push();
rotate(TWO_PI * j2 / 6);
translate(ux*0.25,0);
ellipse(0, 0, 5, 5);
rotate(ang3);
pop();
}
}
pop();
}
}
pop();
}
}
}
This project was inspired by one of the rotation examples this week. During my experimenting, I found some interesting way to arrange the rotating figures. The results remind me of the formation of snowflakes so that’s how it got its name.
As a side note, because the size of the canvas is limited, the snowflakes overlap sometimes, which would influence the visual. Also the display is cropped off because of WordPress.
![[OLD – FALL 2016] 15-104 • COMPUTING for CREATIVE PRACTICE](../../../../wp-content/uploads/2020/08/stop-banner.png)
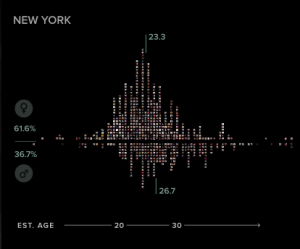
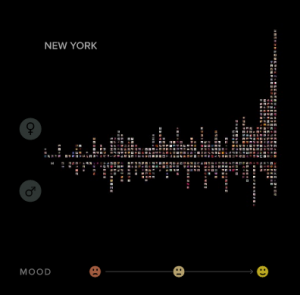

 The picture above was made by a computer program developed by the Slovenian computational artist, Andrej Bauer. The program accepts the name of a picture, which in this case is my name, and generates a random picture using the name as a “seed”. The same “seed” consistently yields the same painting.
The picture above was made by a computer program developed by the Slovenian computational artist, Andrej Bauer. The program accepts the name of a picture, which in this case is my name, and generates a random picture using the name as a “seed”. The same “seed” consistently yields the same painting.




