![[OLD – FALL 2016] 15-104 • COMPUTING for CREATIVE PRACTICE](../../../../wp-content/uploads/2020/08/stop-banner.png)
// Simin Li
// Section C
// siminl@andrew.cmu.edu
// Project 7
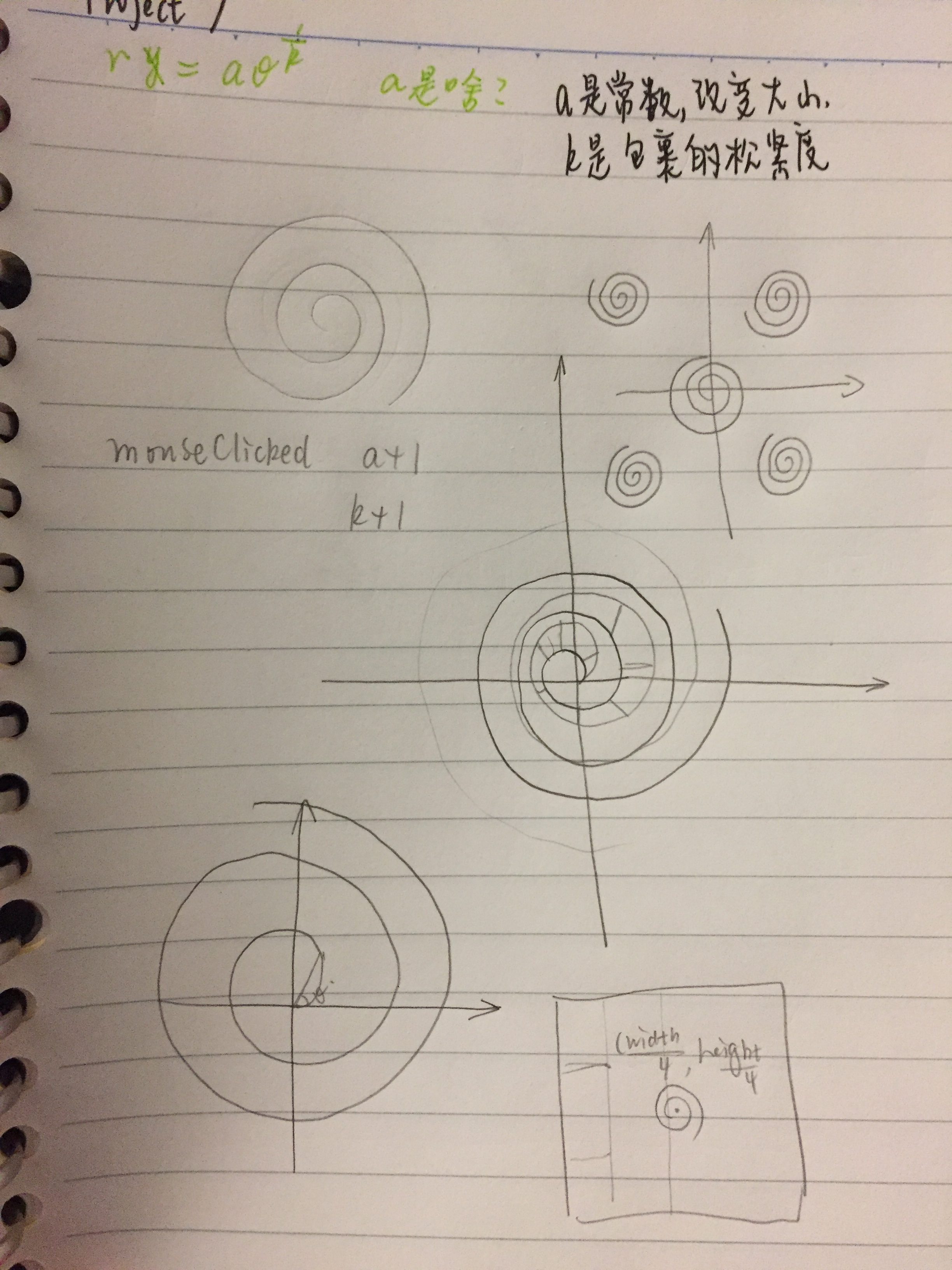
//Archimedean Spiral
//r = a * pow( theta, 1 / n)
var nPoints = 100; //number of points in each individual spiral
var radius; // radius of the polar function
function setup() {
createCanvas(640, 640);
frameRate(8);
}
function draw() {
background(0);
var X = constrain(mouseX,0,width);
var Y = constrain(mouseY,0,height);
//it wont work if cursor is off canvas
var gap1 = map(X , 0, width, 0, 6);
var gap2 = map(X, 0 , width, 4,0);
var ellipseD = map(Y, 0 , height, 0, 4);
var R = map(Y, 0 , height, random(0,255), random(0,255));
var G = map(X, 0 , width, random(0,255), random(0,255));
var B = map(X + Y, 0 , width + height, random(0,255), random(0,255));
//RGB values are randomly selected and then influenced by X and Y to make 3 colors
var angle = map(X,0,width,0,3 * TWO_PI);
color1 = color(R,G,B);
color2 = color(G,R,B);
color3 = color(R,B,G);
//three colors are used to fill the three spirals in the center
spiral(width / 2 ,height / 2,gap1 + 2,ellipseD + 2,color3,angle,1);//largest spiral
spiral(width / 2 ,height / 2,gap1 + 1.2,ellipseD + 1,color2,angle,1);//larger spiral
spiral(width / 2 ,height / 2,gap1,ellipseD ,color1,angle,1); //small spiral
//center spiral group
spiral(width / 4 ,height * 3 / 4,gap2 + 2,2,255,angle,1);
spiral(width / 4 ,height * 3 / 4,gap2 + 1,2,255,angle,1);
spiral(width / 4 ,height * 3 / 4,gap2,2,255,angle,1);
//bottom left spiral group
spiral(width * 3 / 4 ,height * 3 / 4,gap2 + 2,2,255,angle,1);
spiral(width * 3 / 4 ,height * 3 / 4,gap2 + 1,2,255,angle,1);
spiral(width * 3 / 4 ,height * 3 / 4,gap2,2,255,angle,1);
//bottom right spiral group
spiral(width * 3 / 4 ,height / 4,gap2 + 2,2,255,angle,1);
spiral(width * 3 / 4 ,height / 4,gap2 + 1,2,255,angle,1);
spiral(width * 3 / 4 ,height / 4,gap2,2,255,angle,1);
//top right spiral group
spiral(width / 4 ,height / 4,gap2 + 2,2,255,angle,1);
spiral(width / 4 ,height / 4,gap2 + 1,2,255,angle,1);
spiral(width / 4 ,height / 4,gap2,2,255,angle,1);
// top left spiral group
}
function spiral(spiralX,spiralY,gap,ellipseD,shade,angle,tightness){
//draw spiral at spiralX,spiralY
//the gap between each loop is gap
//the diameter of the small circles or squares that make up the spiral is ellipseD
//fill with shade
//rotate by angle
//tightness controls how wound up the spiral is
//when tightness = 1 it is the famous Archimedes' spiral
push()
translate(spiralX, spiralY);
//coordinates of center of spiral
rotate(angle);
for (var i = 0; i < nPoints; i++) {
var theta = map(i, 0, nPoints,0, 6 * TWO_PI);
//map theta so there will be nPoints of squares or circles drawn
radius = gap * pow( theta, 1 / tightness);
var px = radius * cos(theta);
var py = radius * sin(theta);
//coordinates of squares or circles
noStroke();
fill(shade);
if(i % 2 == 0){
rectMode(CENTER);
rect(px - 5, py - 5, ellipseD, ellipseD);}
else{
ellipse(px - 5, py - 5, ellipseD, ellipseD);
}
//alternate squares and circles
}
pop();
}
I searched through the functions provided on math world and selected this spiral because it had a simplicity to it, yet it could have so many different forms. I created this starry night image because spirals remind me of stars. A problem that I had to deal with was that if you put too many circles in a single spiral each ring would align and look less interesting.
