afukuda-project-05-wallpaper
/*
* Name | Ai Fukuda
* Course Section | C
* Email | afukuda@andrew.cmu.edu
* Project | 05
*/
var diamondX // x-coordinate for diamond
var x // horizontal line increment
var y // vertical line increment
function setup() {
createCanvas(400, 480);
}
function draw() {
background(140, 164, 212);
stroke(219, 242, 248);
for (y = 0; y <481; y += 80) {
for (x = 0; x < 481; x += 80) {
// ODD COLUMN GEOMETRY
if (x%160 == 0) { // calling only odd columns
line(x, y, x+80, y); // array horizontal lines
line(x, y+40, x+40, y); // array top-left diamond lines
line(x, y+40, x+40, y+80) // array bottom-left diamond lines
line(x+40, y, x+80, y+40); // array top-right diamond lines
line(x+40, y+80, x+80, y+40); // array bottom-right diamond lines
for (diamondX = 0; diamondX < 41; diamondX += 8) {
if (y%160 == 0) { // from odd columns - calling only odd rows
line(x+40, y, x+diamondX, (y+40)+diamondX); // array fanning-left lines (fan down)
line(x+40, y, (x+40)+diamondX, (y+80)-diamondX); // array fanning-right lines (fan down)
// TURQUOISE TRIANGLE (BOTTOM)
push();
fill(193, 228, 221);
beginShape();
vertex(x, y);
vertex(x+40, y);
vertex(x, y+40);
endShape();
pop();
// LIGHT BLUE TRIANGLE (TOP)
push();
fill(209, 226, 244);
beginShape();
vertex(x, y);
vertex(x, y-40);
vertex(x+40, y);
endShape();
pop();
}
else { // from odd columns - calling now even rows
line(x+40, y+80, x+diamondX, (y+40)-diamondX); // array fanning-left lines (fan up)
line(x+40, y+80, (x+40)+diamondX, y+diamondX); // array fanning-right lines (fan up)
noFill();
ellipse(x-40, y, 138, 80); // array oval
arc(x+40, y-40, 138, 80, 0, PI); // array oval (bottom-half)
arc(x+40, y+40, 138, 80, PI, 0); // array oval (top-half)
// TURQUOISE TRIANGLE (TOP)
push();
fill(193, 228, 221);
beginShape();
vertex(x+40, y+80);
vertex(x+80, y+40);
vertex(x+80, y+80);
endShape();
pop();
// LIGHT BLUE TRIANGLE (BOTTOM)
push();
fill(209, 226, 244);
beginShape();
vertex(x+40, y-80);
vertex(x+80, y-80);
vertex(x+80, y-40);
endShape();
pop();
}
}
}
// EVEN COLUMN GEOMETRY
else {
line(x, y+40, x+80, y+40); // array horizontal lines
line(x, y, x+40, y+40); // array top-left diagonal lines
line(x+40, y+40, x, y+80); // array bottom-left diagonal lines
line(x+40, y+40, x+80, y); // array bottom-right diagonal lines
line(x+40, y+40, x+80, y+80); // array top-right diagonal lines
if (y%160 == 0) { // from even columns - calling only odd rows
line(x, y-40, x, y+40); // array left vertical lines
line(x+80, y-40, x+80, y+40); // array right vertical lines
// ORANGE DIAMOND OFFSET (TOP)
push();
fill(253, 203, 167);
beginShape();
vertex(x, y);
vertex(x+40, y-40);
vertex(x+80, y);
vertex((x+80)-(20/sqrt(2)-5), y+10);
vertex(x+40, y-20);
vertex(x+(20/sqrt(2)-5), y+10);
endShape();
pop();
// PINK ELLIPSE (TOP)
ellipseMode(CENTER);
fill(249, 200, 203);
ellipse(x+40, y+26, 20, 20);
}
else { // from even columns - calling now even rows
// PINK ELLIPSE (BOTTOM)
fill(249, 200, 203);
ellipse(x+40, y-25, 20, 20);
// ORANGE DIAMOND OFFSET (BOTTOM)
push();
fill(253, 203, 167);
beginShape();
vertex(x, y);
vertex(x+(20/sqrt(2)-3), y-10);
vertex(x+40, y+20);
vertex((x+80)-(20/sqrt(2)-5), y-10);
vertex(x+80, y);
vertex(x+40, y+40);
endShape();
pop();
}
}
}
}
} // draw function end bracket
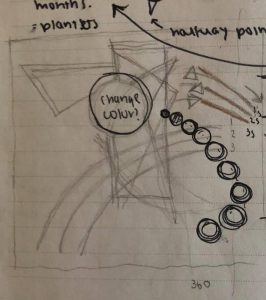
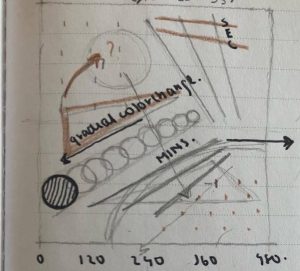
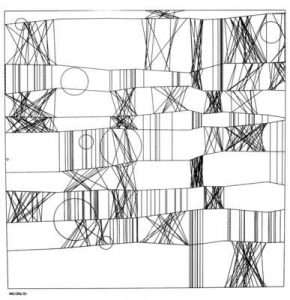
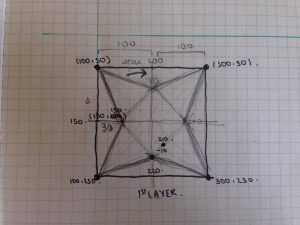
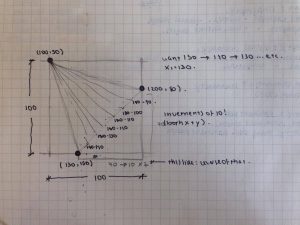
My wallpaper was inspired by this geometric pattern I came across while brainstorming for ideas. One thing I noticed upon completing the base of the pattern, was that while it does exhibit a degree of offset row by row, it still had a very strong vertical presence. In order to mitigate the verticality of the pattern I incorporated the overlapping ellipses to create a floral, petal-like design horizontally across the canvas. Finally I added some colors in specific moments to make the wallpaper stand out more.
![[OLD FALL 2017] 15-104 • Introduction to Computing for Creative Practice](../../../../wp-content/uploads/2020/08/stop-banner.png)



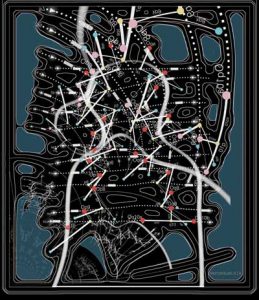

 Bolbemit by Studio Nick Ervinck has a parasitic presence in the chapel, yet it somehow manages to be harmonious as well. This peculiar balance between the innovative and orthodox is what was most memorable and inspirational about this piece of work. While traditionally the ceilings of churches portray biblical scenes, the heavens and so forth, Ervinck challenges this norm through the installation of his modern ‘blob sculptures’. This computer-generated design further questions the rigidity and immobility of architectural structure; as an architecture student I appreciate his inquisitive challenging approach of work. From the almost topographic nature of the Bolbemit, it can be intuitively thought that there is a radial formula involved, with different variables so as to differentiate between the previous geometry. The questioning of the compatibility between virtual and actual space is a recurring theme in the work of Ervinck, and that is clearly reflected in this work as well.
Bolbemit by Studio Nick Ervinck has a parasitic presence in the chapel, yet it somehow manages to be harmonious as well. This peculiar balance between the innovative and orthodox is what was most memorable and inspirational about this piece of work. While traditionally the ceilings of churches portray biblical scenes, the heavens and so forth, Ervinck challenges this norm through the installation of his modern ‘blob sculptures’. This computer-generated design further questions the rigidity and immobility of architectural structure; as an architecture student I appreciate his inquisitive challenging approach of work. From the almost topographic nature of the Bolbemit, it can be intuitively thought that there is a radial formula involved, with different variables so as to differentiate between the previous geometry. The questioning of the compatibility between virtual and actual space is a recurring theme in the work of Ervinck, and that is clearly reflected in this work as well.