My math is a bit rusty so my head spun when perusing the Mathworld website. I first played around with the equations given in the project example, which resulted in this:
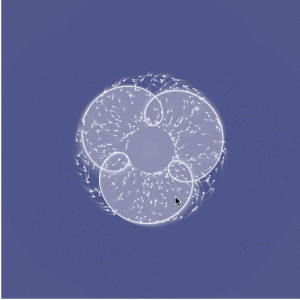
I studied each part of the code until I was able to create another curve. I created a Cartioid Curve that increases size and rotates based on mouseX, and the background also changes based on the mouseX and mouseY positions.
// Tiffany Lai
// 15-104, Section A
// thlai@andrew.cmu.edu
// Project 07 - Curves
var nPoints = 500; // amount of points in curve
function setup() {
createCanvas(480, 480);
}
function draw() {
// background changes colors based on mouse position
var r = map(mouseX, 0, width, 50, 200);
var g = map(mouseY, 0, width, 150, 200);
var b = map(mouseX, 0, height, 200, 255);
background(r - 100, g - 100, b - 100, 130);
drawCurve(); // draw the cardioid curve
}
function drawCurve(){
//mathworld.wolfram.com/Cardioid.html
var x; // defining x and y positions of vertices in curve
var y;
var a = map(mouseX, 0, width, 0, 100); // map mouseX from 0 to 5
fill(100, 200, 255, 20); // blue
stroke(255); // white
translate(width/2, height/2);
beginShape();
for (var i = 0; i < nPoints; i++) {
var t = map(i, 0, nPoints, 0, TWO_PI);
x = a * (1 + cos(t)) * cos(t); // parametric equation of cardioid
y = a * (1 + cos(t)) * sin(t); // parametric equation of cardioid
rotate(radians(mouseX/500)); // rotate based on mouseX
ellipse(x, y, 1, 1); // draw spiral of dots
vertex(x, y); // draw the first curve (blue)
}
endShape();
beginShape();
for (var i = 0; i < nPoints; i++) {
var t = map(i, 0, nPoints, 0, TWO_PI);
x2 = a * (1 + cos(t)) * cos(t); // parametric equation of cardioid
y2 = a * (1 + cos(t)) * sin(t); // parametric equation of cardioid
rotate(radians(mouseX/500)); // rotate based on mouseX
fill(255, 150, 150, 20); // pink
vertex(x2, y2); // draw the second curve (pink)
}
endShape();
}
![[OLD FALL 2017] 15-104 • Introduction to Computing for Creative Practice](wp-content/uploads/2020/08/stop-banner.png)