//Max Stropkay
//Section E
//mstropka@andrew.cmu.edu
//Project_07
var nPoints = 1000;
function setup() {
createCanvas(480, 480);
}
function drawEpicycloid(){
// x = (R+r)cos theta - r cos((R+r)/r)theta)
// y = (R + r)sin theta - rsin(((R+r)/r)theta)
var R = 100 //radius of large circle
var r = 10 //radius of small circle
var a = mouseX //take values of mouse x
var b = mouseY //take values of mouse y
//draw curve in center of screen
push();
translate(240, 240)
noFill();
strokeWeight(.01);
//draw curve
beginShape();
for(var i = 0; i < nPoints; i++){
var t = map(i, 0, nPoints, 0, TWO_PI);
var x = (a + r)*cos(t) - (r)*cos(((a + b)/r)*(t))
var y = (b + r)*sin(t) - (r)*sin(((a + b)/r)*(t))
//points of curve will be drawn at somewhere within 50 pixels of (x,y)
vertex(x + random(-50, 50),y + random(50, - 50));
}
endShape(CLOSE);
pop();
}
function draw(){
drawEpicycloid();
}
//redraw background if the mouse is pressed
function mousePressed(){
background(255);
}
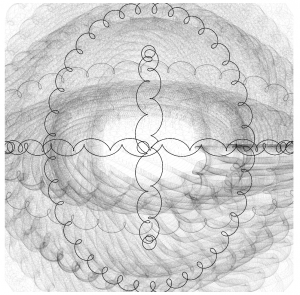
For this assignment, I used the equation for an epicycloid with the mouse’s location driving certain variables to change the shape as the mouse moves. I can’t say I understand the equation for this type of curve that well so I just started substituting the mouseX and mouse Y value for random variables in the equation until I got something that looked cool. I also added a random value to the x and y coordinates of the points that the program draws.
Here is a screenshot from before I added the random values to the x and y coordinates.
![[OLD FALL 2017] 15-104 • Introduction to Computing for Creative Practice](wp-content/uploads/2020/08/stop-banner.png)