Category: SectionD

Stefanie Suk – Project 07 – Curves

sketch

//Stefanie Suk
//15-104 D
//ssuk@andrew.cmu.edu
//Project - 07 - Curves

var nPoints = 100;

function setup() {
    createCanvas(400, 400);
}


function draw() {

    fill(20, 8, 78); //color for background
    rect(0, 0, width, height); 
    
    push();
    translate(width / 1.4, height / 2);
    drawCurve();
    pop();

}

function drawCurve() {
    var cR = map(mouseX, 0, width, 100, 200);
    var cG = map(mouseX, 0, width, 200, 250);
    var cB = map(mouseX, 0, width, 230, 255); //color for shape

    var s = 100; // size
    var a = constrain(mouseX/2, 0, width) / 30; // mousex position
    var b = constrain(mouseY/2, 0, height) / 30; // mousey position

    fill(cR, cB, cG);
    strokeWeight(5);
    stroke(255);

    beginShape(); 
    for (var i = 0; i < nPoints; i++){ 
    var t = map(i, 0, nPoints, 0, TWO_PI); 

    x = s * (cos(a+t) * (1-(cos(a+t))));
    y = s * (sin(b+t) * (1-(cos(b+t)))); // equation of curve to create shape

    vertex(x,y);// drawing vertex
  }
  endShape(CLOSE); 
}

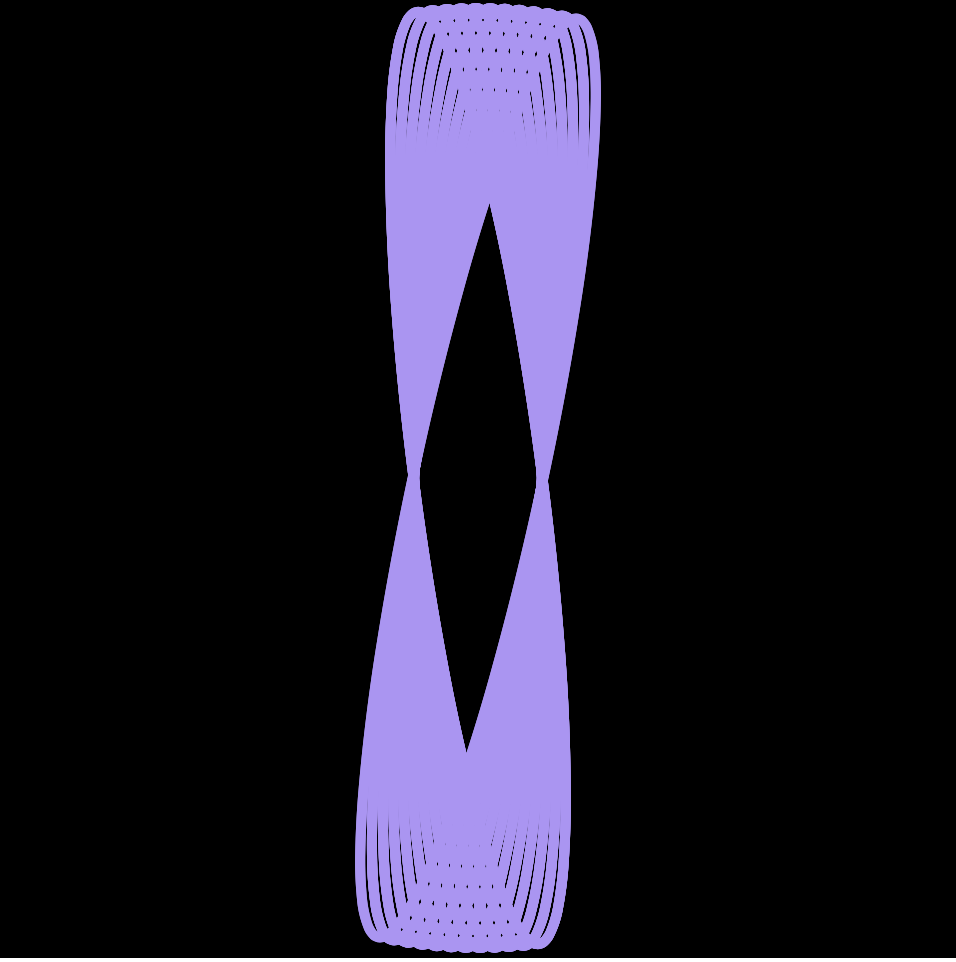
I used the Cardioid Curve from the Mathworld curves site to create this project. At first, I thought the movement of the curve was interesting, which is why I chose to use this particular curve. I thought the circular movement of the curve looked like the tornado-like movement of water when it is spun. I tried to express that circular movement of water with cardioid. By making the background color dark blue and the shape itself change colors between different shades of blue, I tried to express water and the spiral movement of water. Everytime I move the mouse left, the shape will turn clockwise and the color will turn vivid blue-green. When the mouse is moved right, the shape will turn counter-clockwise and the color will turn light blue.

Stefanie Suk – Looking Outwards – 07

Installation of Unnumbered Sparks in Vancouver, Canada

Unnumbered Sparks, a work by Aaron Koblin and Janet Echelman, is a monumental interactive sculpture installed in the sky. This sculpture is a crowd-controlled visual artwork on a large canvas, where the color and design on the sculpture is choreographed by visitors at the moment through their mobile device. The visitors were able to use their smartphones and tablets to paint colors of light across the installation. Every small movement of the electronic devices projected vivid beans of light across the sculpture. What I admire the most about this artwork is the scale and complexity achieved in a single piece of installation. The computational software used in this sculpture explores scale, density, shape, and interaction with people, which I thought was the most fascinating about this project. Thus, the material used in this installation also caught my attention. The whole sculpture is made out of soft fibers attached directly into existing buildings. This exploration of material and application of interaction technology, I thought, really showed how much the artists wanted people to feel projected/connected to their artwork. This sculpture was definitely successful in using computation technology to create interaction between artwork and the visitors. 

Video of Unnumbered Sparks in Vancouver, Canada

Shannon Ha – Looking Outwards 07

Photo taken from jevbratt.com

‘Migration’ by Lisa Jevbratt is a data visualization image of the Internet. Each pixel represents 256 IP addresses and the different positions, size, color of the pixel blobs represents the amount of websites. This database of Websites was created by searching for Websites in the same IP addresses three times throughout 1999, 2001, 2004. The patterns in these images reveal  both the search process and information about the Internet and the Web. What I admire most about this piece of work is how it shows change over time in our ‘technology carbon footprint’ through the way the visual representations intensify which goes to show how dependent we have become on The Web. It is also very interesting how we can click into the blobs which would link and redirect you to the Website IP address, this way, the data visualized isn’t only presented on a surface level, but also lets us interact with it.

Cathy Dong-Looking Outwards-07

Flight Pattern Visualization

Originally developed by Scott Hessels and Gabriel Dunne, “Celestial Mechanics” project used Adobe After Effects and Maya. With time lapse animation, the project visualizes air traffic data and turns it into a series of videos and drawings, and perhaps art. Through still 2D drawings and screen captures, it displays the dynamics. Information shows the origin, end and path of the journey. Comparing the density of parts, readers find the busier ports in North America within a period of twenty-four hours. Also as it reveals multiple iterations of multiple iterations of flight patterns during the cycle, the project implies weather systems and no-fly zones.

Air Traffic over North America
Zoom-in Flight Pattern

Cathy Dong-07-Curve

sketch

/* Cathy Dong
   Section D
   yinhuid@andrew.cmu.edu
   Project 07 - Composition with Curves
*/

var density = 200;

function setup() {
    createCanvas(480, 480);
}

function draw() {
    background(0);
    stroke(255);
    noFill();

    //call devil's curve
    strokeWeight(1);
    push();
    translate(width/ 2, height / 2);
    devilDraw()
    pop();

    //call curve and make its center move with mouse
    strokeWeight(.5);
    push();
    var xDraw = constrain(mouseX, width / 5, width / 5 * 4);
    var yDraw = constrain(mouseY, width / 8, height / 8 * 7);
    translate(xDraw, yDraw);
    hypocycloidDraw();
    pop();
}

//draw hypocycloid move with mouse
function hypocycloidDraw() {
    var xA;
    var yA;
    var aA = map(mouseX, 0, width, 0, width / 5);
    var bA = map(mouseY, 0, height, 0, height / 8);
    beginShape();
    for (var i = 0; i < density; i++) {
        var t = map(i, 0, density, 0 ,PI * 2);
        xA = (aA - bA) * cos(t) - bA * cos((aA - bA) * t);
        yA = (aA - bA) * sin(t) - bA * sin((aA - bA) * t);
        vertex(xA, yA);
    }
    endShape();
}

// draw devil's curve function
function devilDraw() {
    var xD;
    var yD;
    var aD = map(mouseX, 0, width, 10, width/ 8);
    var bD = map(mouseY, 0, height, 10, height / 10);
    beginShape();
    for (var j = 0; j < density; j++) {
        var t = map(j, 0 , density, 0, PI * 2);
        xD = cos(t) * sqrt((pow(aD, 2) * pow(sin(t), 2) - pow(bD, 2) * pow(cos(t), 2)) / (pow(sin(t), 2) - pow(cos(t), 2)));
        yD = sin(t) * sqrt((pow(aD, 2) * pow(sin(t), 2) - pow(bD, 2) * pow(cos(t), 2)) / (pow(sin(t), 2) - pow(cos(t), 2)));
        vertex(xD, yD);
    }
    endShape();
}

mouse bottom left
mouse upper left

I started the project with browsing Mathworld Curves and found the curves that I am interested in. I used devil’s curve and hypocycloid. Devil’s curve remains at canvas center and its long diagonal edges change side when mouse moves, whereas hypocyloid itself flies with mouseX and mouseY. Hypocyloid is the smallest when it’s at upper left corner and largest at lower left. It is less complex and mouse moves to left of the canvas. The longest devil curve edges and the hypocyloid would only appear to be at the same edge when mouse is at upper right.

Sarah Choi – Project 07 – Composition with Curves

project-07

//Sarah Choi 
//Section D
//sychoi@andrew.cmu.edu
//Project-07

var col;

function setup() {
    createCanvas(400, 400);
}

function draw() {
    background(0);

    //randomize color
    col = color(random(255), random(255), random(255));

    x = constrain(mouseX, 0, width);
    y = constrain(mouseY, 0, height);
    
    // draw the frame
    fill(255); 
    noStroke();
    text("The Butterfly", 20, 40);
    stroke(255);
    noFill(); 
    rect(0, 0, width-1, height-1); 
    
    // draw the curve, rotate on mouseX
    push();
    translate(width / 2, height / 2);
    rotate(map(mouseX, 0, width, 0, 1));
    drawButterfly();
    pop();
}

//--------------------------------------------------
function drawButterfly() {
    // Butterfly Curve:
    // http://mathworld.wolfram.com/ButterflyCurve.html
 
    //adding variability and movement
    var m = (map(x, 0, mouseY, 0, width)); 
    var m = (map(y, 0, mouseX, 0, height));

    stroke(255);
    fill(col);

    beginShape();
    for (var i = 0; i < 300; i++) {
        var t = map(i, 0, 300, 0, 2 * TWO_PI);
        
    //butterfly curve equations
        r = (exp(cos(t))) - (2 * cos(4 * t)) + (sin((1 / 12) * t));

        x = r * sin(t) * m
        y = r * cos(t) * m
        vertex(x, y)
    }
    endShape(CLOSE);
}

I chose a curve that could turn on an angle. Thinking of fully randomizing and creating something abstract on the basis of mathematics was my main goal for this project. Because we have been focusing and reflecting on computational art, I wanted to be able to portray this with my own work. It was interesting to play around with the variables as they made a big difference in how the curve was portrayed.

Below, I have shown three different aspects of the curve showing the beginning and how it manifests as it follows the x and y coordinates of the mouse. I wanted to show portray nature by showing the beginning of a butterfly as pure blackness. As one moves the mouse, the shapes get bigger with colors constantly changing showing the beauty butterflies bring into our world. As the mouse moves more across the screen, the butterfly gets bigger to depict what the human eye takes in as a butterfly flies closer to him or her.

Kristine Kim – Project 07 – Curves

sketch

//Kristine Kim
//Section D
//younsook@andrew.cmu.edu
//Project- 07- Curves
var nPoints = 70

function setup() {
    createCanvas(480, 480);
    frameRate(10);
}

function draw() {
    background(67, 42, 135);
    //calling all the functions 
    //drawing all of them on the center of the canvas

    push();
    translate(width/2, height/2);
    drawMovinglines();
    drawHypotrochoid();
    drawEpitrochoidCurve();   
    pop();
}

/*drawing the EpitrochoidCurve filled with
colors that are determined by mouseX and mouseY */
//the image that is drawing on top of everything
function drawEpitrochoidCurve(){

    var x;
    var y;

    var r1 = 100
    var r2 = r1 / mouseX;
    var h = constrain(mouseX, r1 , r2) 
    noStroke();
    fill(mouseY, 245, mouseX);
    beginShape();
    //for loop to draw the epitrochoidcurve
    for (var i = 0; i < nPoints; i++){
        var t = map(i, 0, nPoints, 0, TWO_PI);
        x = (r1 + r2) * cos(t) - h * cos(t * (r1 + r2) / r2);
        y = (r1 + r2) * sin(t) - h * sin(t * (r1 + r2) / r2);
        vertex (x,y);
    }
    endShape(CLOSE);
}
/*drawing the hypotrochoid with vertexs with
colors determined by mouseY */
//the first layer, drawing behind the epitrochoidcurve and movinglines

function drawHypotrochoid(){
    var x;
    var y;

    var r1 = 250
    var r2 = r1/ mouseX;
    var h = constrain(mouseY, r1, r2)
    stroke(mouseY, 200, 73);
    noFill();
    beginShape();
    //for loop for drawing the hypotrochoid form
    for (var i = 0; i < nPoints; i ++){
        var t = map(i, 0, nPoints, 0 , TWO_PI);
        x = (r1- r2) * cos(t) + h * cos(t * (r1 - r2) / r2);
        y = (r1- r2) * sin(t) + h * sin(t * (r1 - r2) / r2);
        vertex(x,y)
    }
    endShape(CLOSE);
}
/*drawing the constiently moving/wiggling circle
the radius and fill all controlled by mouseX and mouseY
the second layer, between the epitrochoidcurve and hypotrochoid */

function drawMovinglines(){
    var x;
    var y;
    var r1 = mouseX
    fill(mouseX, mouseY, mouseX)

    beginShape();
    //for loop for drawing the wiggling circle
    for (var i = 0; i < nPoints; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        var x = r1 * cos(t);
        var y = r1 * sin(t);
        vertex(x + random(-5, 5), y + random(-5, 5));
    }
    endShape(CLOSE);

}

I was first very intimidated by this project because it looked so complicated and intricate, but I studying the website provided to us was very helpful. The little explanations and gif helped me understand the concept a lot. There are just so many ways we can execute this project so I struggled with starting the project, but once I drew the Hypotrochoid function, I knew how to approach this project. I played around with the quantity of nPoints, fill(), stroke(), and a lot with mouseX and mouseY until I ended up with the product that I have right now . I enjoyed creating this a lot because I love discovering new images and findings so I was pleasantly surprised every single time I changed something in my code and found different drawings.

Lauren Park – Project – 07 – Curves

sketch

//Lauren Park
//ljpark@andrew.cmu.edu
//Section D
//Project-07-Curves

function setup() {
  createCanvas(480, 480);
}

function draw() {
  background(10);
  
  drawHypotrochoid();
  drawHypocycloid();
}

function drawHypotrochoid() {
  var x;
  var y;
  
  //mouse controls color change for stroke
  var r = constrain(mouseX, 0, 300);
  var g = constrain(mouseY, 0, 300);
  var b = 150;
  
  push();
  fill('#53E9FF');
  stroke(r, g, b);
  strokeWeight(3);
  translate(width/2, height/2);
  
  //control hypotrochoid
  var ha1 = map(r, 0, width, 0, 100);
  var ha2 = map(g, 0, height, 0, 100);
  
  beginShape();
  for (var i = 0; i < 480; i+=3) {
    var angle1 = map(i, 0, 250, 0, 360);
  
  //equation of hypotrochoid from MathWorld curves site
  x = (ha1 - ha2)* cos(angle1) + b * cos((ha1 - ha2 * angle1));
  y = (ha1 - ha2)* sin(angle1) - b * sin((ha1 - ha2 * angle1));
  vertex(x, y);
  }
  endShape();
  pop();
}

function drawHypocycloid() {
  var x;
  var y;
  
  //mouse controls color change for stroke
  var r = map(mouseX, 0, width, 50, 255);
  var g = map(mouseY, 0, height, 50, 255);
  
  push();
  fill(254, 193, 255, 140);
  stroke(r, g, 255);
  strokeWeight(0.3);
  translate(width/2, height/2);
  
  //control hypocycloid
  var hy1 = map(mouseX, 0, width, 0, 300);
  var hy2 = map(mouseY, 0, height, 0, 300);
  
  beginShape();
  for (var a = 0; a < 200; a+=3) {
    var angle2 = map(a, 0, 100, 0, 360);
    
    //equation of hypocycloid from MathWorld curves site
    x = (hy1 + hy2)* cos(angle2) + hy2* cos((hy1 + hy2)*angle2);
    y = (hy1 + hy2)* sin(angle2) - hy2* sin((hy1 + hy2)*angle2);
    vertex(x, y);
  }
  endShape();
  pop();
}

My idea for this project initially came from visuals of a rotating flower. However, throughout this process of figuring out this project, I became more interested in intricate patterns within this flower shape. And so, I was more focused on adding different color changes and perspectives when the mouse moves, to show off different designs of this form. When the mouse is somewhere near the top left edge of the canvas, I want to show the two different curves separately to represent seed-like forms, so that when the mouse moves in other directions, then the flower can gradually grow and spread to a wider view. Overall, it was very challenging but very satisfying to create patterns that remind of the kaleidoscope effect.

Lauren Park – Looking Outwards – 07

Artist Aaron Koblin visualized using bright colors and overlapping shapes to mark the many different pathways across North America by air travel. This project was originally developed by Scott Hessels and Gabriel Dunne for a project called “Celestial Mechanics” and uses data from the US Federal Aviation Administration (FAA) to help track these planes. This piece conceptualizes these pathways for over a 24 hour period.

I enjoy the visuals of this time-lapse animation piece because these colorful routes remind me of fireworks and show where each route starts and ends. It also paints a bigger picture for me to see how much the US relies on planes and how many airports we have. With the data collected from the FAA, the information was translated into these visuals through an open source programming called Processing.

The artist was highly successful in effectively displaying and color coding flights depending on each different type of flight. In contrast with the dark background, these bright colors also depict the relationship between humans and the technology we rely on. The way these pathways all come together to form a broad shape of the US is really powerful in communicating to viewers that we are systematically a part of this process of air travel.

“Flight Pattern” time-lapse animation (2005) by Aaron Koblin
Flight Patterns

Monica Chang- Project-07-Curves

sketch

//Monica Chang
//mjchang@andrew.cmu.edu
//Section D
//Project-07-Curves

var nPoints = 100;
var radiusX;
var radiusY;
var separation = 125;

function setup() {
    createCanvas(480, 480);
  
}

function draw() {
    background("darkcyan");
    fill(255, 255, 255, 64);
    
    radiusX = mouseX;
    radiusY = mouseY;

    drawCircles();
    drawEpitrochoidCurve();
    drawDeltoid();
}

//circle elements

function drawCircles() {
  
  // a sequence of little, circle elements
    push();
    translate(width / 2, height / 2);
    for (var i = 0; i < nPoints + 10; i++) {
        var theta = map(i, 0, nPoints, 0, TWO_PI);
        var px = radiusX / 2 * cos(theta);
        var py = radiusY / 2 * sin(theta);
      
        stroke("lightcyan");
        strokeWeight(1);
        circle(px - 5, py - 5, 8, 8);
    }
    pop();
  
}


function drawDeltoid() {
    //Deltoid:
    //http://mathworld.wolfram.com/Deltoid.html
    beginShape();
    nPoints = 40;
    for (var i = 0; i < nPoints; i++) {   
    	var angle = map(i, 0, 180, 0, 360);
        var radius = 70;
        var a = map(mouseX, 0, height, 5, 80)
        var b = map(mouseY, 0, height, 5, 90)
        
        //x-coordinate for deltoid
        var x = (a - b) * cos(angle) + radius * cos((a - b * angle));
        //y-coordinate for deltoid
        var y = (a - b) * sin(angle) - radius * sin((a - b * angle));
        rotate(radians(angle));
        noFill();
        strokeWeight(3);
        stroke("red");
        vertex(x, y);
      }
    endShape();
    

}

function drawEpitrochoidCurve() {
    // Epicycloid:
    // http://mathworld.wolfram.com/Epicycloid.html
    
    var x2;
    var y2;
    
    var a = 80.0;
    var b = a / 2.0;
    var h = constrain(mouseY / 8.0, 0, b);
    var ph = mouseX / 30.0;
    
    noFill();
    stroke("tan");
    strokeWeight(1);
    beginShape();
    translate(width / 2, height / 2);
    for (var i = 0; i < nPoints + 10; i++) {
        var t = map(i, 0, nPoints, 0, TWO_PI);
        
        x2 = (a + b) * cos(t) - h * cos(ph + t * (a + b) / b);
        y2 = (a + b) * sin(t) - h * sin(ph + t * (a + b) / b);
      
        //switching x and y-coordinates to create a band of waves/
        vertex(x2, y2);
        vertex(y2, x2);
    }
    endShape(CLOSE);
    
}

Bottom Left
Bottom Right
Top Left
Top Right

This project definitely had me studying the formulas 75% of the time for me to really start putting anything together. However, once I got the gist of the formulas, it was really entertaining for me. I began with studying the deltoid curve and I realized this particular curve created so many different shapes. Thus, I wanted to provide a more constant curve which became the sequence of circles which are relatively more static to create a sense of balance.