Category: SectionD

Raymond Pai-Project 07 – Composition with Curves

sketch

///RAYMOND PAI
///SECTION D
///RPAI@ANDREW.CMU.EDU
///PROJECT 07

function setup(){
    createCanvas(480, 480);
}

function draw() {
    background(mouseX, mouseY, mouseX);
    //Draw Curves 1 and 2
    drawE1();
    drawE2();
    drawE3();
    drawE4();
}

function drawE1() {
    push();
    //Color
    fill(mouseX + 50, 50, mouseY + 50);
    //Center
    translate(width / 2, height / 2);
    var a = map(mouseX, 0, width, 0, 250);
    var b = map(mouseY, 0 , height, 0, 250);
    beginShape();
        for (var i = 0; i < 250; i++) {
            //Angle
            var t = map(i, 0, 250, 0, 2 * PI);
            //Epicycloid equations
            x = (a + b) * sin(t) - b * sin((a + b) * t / b);
            y = (a + b) * cos(t) - b * cos((a + b) * t / b);
            vertex(x, y);
        }
    endShape();
    pop();
}

function drawE2() {
    push();
    //Color
    fill(0, mouseX + 50, mouseY + 50);
    //Center
    translate(width / 2, height / 2);
    var a = map(height-mouseX, 0, width, 0, 250);
    var b = map(height-mouseY, 0 , height, 0, 250);
    beginShape();
        for (var i = 0; i < 250; i++) {
            //Angle
            var t = map(i, 0, 250, 0, 2 * PI);
            //Epicycloid equations
            x = (a + b) * sin(t) - b * sin((a + b) * t / b);
            y = (a + b) * cos(t) - b * cos((a + b) * t / b);
            vertex(x, y);
        }
    endShape();
    pop();
}

function drawE3() {
    push();
    //Color
    fill(200, mouseY + 50, mouseX + 50);
    //Center
    translate(width / 2, height / 2);
    var a = map(height/2-mouseX, 0, width, 0, 250);
    var b = map(height/2-mouseY, 0 , height, 0, 250);
    beginShape();
        for (var i = 0; i < 250; i++) {
            //Angle
            var t = map(i, 0, 250, 0, 2 * PI);
            //Epicycloid equations
            x = (a + b) * sin(t) - b * sin((a + b) * t / b);
            y = (a + b) * cos(t) - b * cos((a + b) * t / b);
            vertex(x, y);
        }
    endShape();
    pop();
}

function drawE4() {
    push();
    //Color
    fill(mouseX + 50, mouseX + 50, 200);
    //Center
    translate(width / 2, height / 2);
    var a = map(height/1.5-mouseX, 0, width, 0, 250);
    var b = map(height/1.5-mouseY, 0 , height, 0, 250);
    beginShape();
        for (var i = 0; i < 250; i++) {
            //Angle
            var t = map(i, 0, 250, 0, 2 * PI);
            //Epicycloid equations
            x = (a + b) * sin(t) - b * sin((a + b) * t / b);
            y = (a + b) * cos(t) - b * cos((a + b) * t / b);
            vertex(x, y);
        }
    endShape();
    pop();
}

Flower Power!

The curve I used is the Epicycloid. I like how it creates petals that resemble flowers.

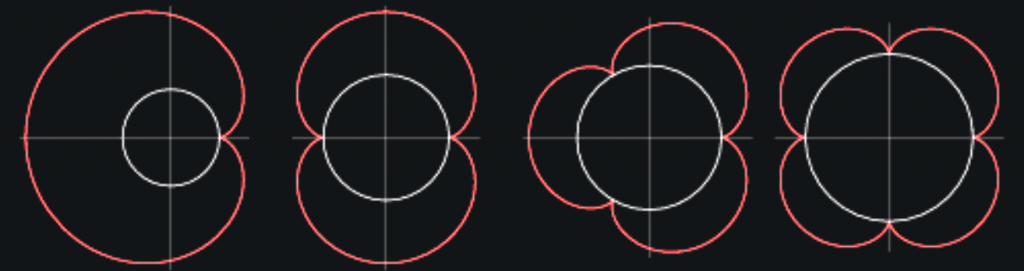
I used 4 Epicycloids of varying sizes to create the effect of flowers without making it obvious that they’re flowers. I decided to do this because the flowers looked pretty lonely.

Lonely Flower

The more curves I added the more interesting the floral patterns became.

The colors are based on the mouse position, but I limited them slightly to more pastel and ‘Spring’ colors, such as pink, green, yellow, etc.

The final product is an abstract and colorful depiction of flowers. Sometimes the flowers invert and create interesting sharp objects, like thorns of a rose. They also contribute to more detailed flowers, such as the process image above.

Sammie Kim–Project 07–Curves

sketch

//Sammie Kim
//Section D
//sammiek@andrew.cmu.edu
//Project 07 - Curves
var nPoints = 360;

function setup() {
    createCanvas(480, 480);
}

function draw() {
    background(0);
    drawHypotrochoid();
    drawAstroid();
}

function drawHypotrochoid() {
    //constraining mouse within the canvas size
    var x = constrain(mouseX, 0, width);
    var y = constrain(mouseY, 0, height);
    //stroke color will also change based on the direction of mouse
    var rColor = map(mouseX, 0, width, 0, 230)
    var gColor = map(mouseY, 0, height, 0, 230)
    stroke(rColor, gColor, 200);
    strokeWeight(2);
    noFill();
    //Setting the parameters for the hypotrocoid
    push();
    translate(width/2, height/2); //starting the shape at the center of canvas
    var a = map(mouseX, 0, width, 0, 200); //the radius range of circle
    var b = map(mouseY, 0, height, 0, 50);
    var h = map(mouseX, 0, height, 0, 50);
    beginShape();
    //Hypotrochoid formula
    //http://mathworld.wolfram.com/Hypotrochoid.html
    for(var i = 0; i <= nPoints; i++) {
        var x = (a - b) * cos(i) + h * cos((a - b) / b * i);
        var y = (a - b) * sin(i) - h * sin((a - b) / b * i);
        vertex(x, y);
    }
    endShape();
    pop();
}

function drawAstroid(){
    var x = constrain(mouseX, 0, width);
    var y = constrain(mouseY, 0, height);
    push();
    noFill();
    strokeWeight(4);
    stroke("pink");
    translate(width / 2, height / 2);
    var a = map(mouseX, 0, width, 20, width / 3);
    beginShape();
    //Astroid formula
    //http://mathworld.wolfram.com/Astroid.html
    for (var i = 0; i < nPoints; i+= 0.5){
        var x = a * pow(cos(i), 3);
        var y = a * pow(sin(i), 3);
        vertex(x, y);
    }
    endShape();
    pop();
}

This project was challenging as I had to incorporate an interactive element within the hypotrochoid shape. It initially took a while to understand how I could flexibly use the map function, substituting different numbers to play with the range of mouse X and Y, then seeing the effects on screen. I also added a change to color as another element, where the R and G values would change depending on the mouse’s location. Afterwards, I created an astroid in the center that playfully interacts with the surrounding hypotrochoid. What intrigued me the most was how unexpected the shape would vastly change by rotating my mouse around the canvas, creating diverse shapes through intersection of lines.

When the max range of hypotrochoid value a is at (0, 10)
When the max range of hypotrochoid value a is at (0, 300)

Ian Kaneko LO – 07

Visual of United States immigration trends

The project I chose was a visual representation of immigration trends done by Pedro M. Cruz and John Wihbey. Both of whom are researchers based at Northeastern University. This project shows immigration trends to the United States based off of the immigrants’ place of birth.

They stated that they were inspired by the way we can see trends in natural history through the rings of a tree. I thought this was a very clear and creative way to represent their data because of the way it shows large trends rather than specific data points.

Each ring of the tree represents 10 years and each color is a region that immigrants are from. The creators obviously took time to make sure it looked visually appealing, through their choice of color and texture. I was not able to transfer the text of the key over to this post, so I highly encourage anyone interested to follow the link posted below.

https://www.nationalgeographic.com/culture/2018/07/graphic-united-states-immigration-origins-rings-tree-culture/

Ian Kaneko Project-07-Curves

Honestly I had very little idea of what I was doing or where I was going with this project. In the end I just experimented around with different equations until I found something that looked cool. The background of my project is a failed attempt at adding more complex curve. However I kind of liked the randomness that it added so I decided to keep it around. I added a cruciform on top of it which ended up having a very interesting shaped fill space. To finish it off I added a “+” to the center that would rapidly spin, making it look circular.

ikaneko Curves



function setup() {
  createCanvas(480, 480);
}

function draw() {
  background(0);

  squiggles();

  drawCruciform();

  drawSpinner();
  

}

// function for background squiggles
function squiggles() {
  strokeWeight(10);
  var x;
  var y;
  var a = width / 2;
  var nPoints = map(mouseY, 0, height, height / 4, height / 2); // It jiggles with y movement
  
  push()
  translate(width / 2, height / 2); // Puts the jumble in the middle of the canvas
  beginShape();
  for (i = 0; i < nPoints; i++) {
    stroke(250, i, 200);
    var t = map(i, 0, nPoints, 0, 2 * PI);  
    x = a * cos(t * (1 - 2 * pow(sin(t), 2))); // Attempted equations
    y = a * sin(t * (1 + 2 * pow(cos(t), 2))); // These didn't turn out how I expected but kinda liked them
    vertex(x, y);
    }
  endShape();
  pop();
 }

 // function for the cruciform
  function drawCruciform() {
    var x;
    var y;
    var a = map(mouseX, 0, width, width / 8, 200); // They move with the mouse
    var b = map(mouseY, 0, height, height / 8, 200);
    var nPoints = 300;
    strokeWeight(20);
    fill(150, 100, mouseX * mouseY / 300); // The interesting fill shape changes color

    translate(width / 2, height / 2); // Centers it around the middle of the canvas
    beginShape();
    
      for(z = 0; z < nPoints; z ++) {
        t = map(z, 0, nPoints, 0, 2 * PI);
        x = a * (1 / cos(t)); // Cruciform equations
        y = b * (1 / sin(t));
        
        vertex(x, y);

      }
    endShape();

    
  }

  function drawSpinner() { // Adds two rectangles to the cent that spin with mouse movement
    fill(200, 250, 200);
    push();
    rotate(mouseX * 10); // Spins very rapidly
    rectMode(CENTER);
    rect(0, 0, 50, 120); // These are already using the same translation as the cruciform
    rect(0, 0, 120, 50);
    pop();
  }

Kristine Kim – Looking Outward – 07

Emoto installation , Studio NAND

Emoto Installation, created by Studio NAND, is a  computational information visualization project that executes the global response/data collected from  Twitter around the London 2012 Olympic Games in an interactive online visualization and physical data sculpture. Based on approximately 12.5 million Twitter messages which were collected in real-time, this project recorded trending topics and how they were discussed online in an interactive visualization which was running live during the same time as the Games in July and August 2012. Each Tweet was annotated with a sentiment score by the project’s infrastructure using software provided by Lexalytics. This data formed the basis for an extensive profiling of London2012 which was finally documented in this interactive installation and physical data sculpture at the WE PLAY closing exhibition of the Cultural Olympiad in the Northwest. I was drawn into this installation because not only it was executed well online, but it was also presented in a physical form/installation.  It was easily recognizable and accesible to understand the project and the data visualization.  The video captures the intentions and content of the project really well and it helped me to understand Emoto Installation more. I love the details of the usage of light projection, color, laser cut, and text all incorporated very well into one installation. I admire the level of detail and effort that was put into this project, the depth of the research and data visualization is very inspiring. 

Emoto Installation Video, Studio NAND

CJ Walsh – Looking Outwards 07 – Data Visualization

6 charts created for (En)tangled Word Bank (2009)

The piece I chose this week is a collaboration between Stefanie Posavec and Greg McInerny. These pieces were created by analyzing insertions and deletions that occurred between six editions of The Origin of Species by Charles Darwin. On her website, Posavec outlines that McInerny completed all of the programming and gathering of data and together they worked on the visual form. While it does not describe the particulars of the programming used to analyze all of the editions, it says that C++ and R were used in terms of programming languages. My guess is that an algorithm was used that analyzed all the sentences within each edition and then checked how many times that sentence was seen again in future versions.

Posavec modeled this form after another project that she did while working on her Masters in Communication Design. She calls the structure a ‘literary organism.’ Each diagram represents an edition, which is then broken down into chapters and subchapters. After that, the subchapters are divided into the paragraph ‘leaves,’ which are then broken into sentence ‘leaflets.’ The sentences in each edition are colored to indicate whether they survive to the next edition (blue) or have removed (orange).

Banners created for Darwin Anniversary Festival at the University of Cambridge

I enjoyed this project because it’s not a dataset that would come to mind when I think about content usually depicted in data visualization. It is interesting to see the way that the content within the editions changes over time. It shows a progression in both scientific thought and how Darwin was developing his theories and knowledge. I think that the form is also pretty interesting. It feels heavily inspired by natural forms and the way that natural species are charted based on relations.

Sources: http://www.stefanieposavec.com/entangled-word-bank https://www.moma.org/interactives/exhibitions/2011/talktome/objects/145525/

Lanna Lang – Project 07 – Curves

sketch

//Lanna Lang
//Section D
//lannal@andrew.cmu.edu
//Project 07 - Curves

var nPoints = 100;
var angle = 0;

function setup() {
    createCanvas(480, 480);
}

function draw() {
    background('#ffc5a1'); //pastel orange
    
    //call, translate, and rotate
    //the epitrochoid curve
    push();
    translate(width/2, height/2);
    rotate(radians(angle));
    drawEpitrochoid();
    angle += 10;
    pop();
    
    //call and translate the hypotrochoid curve
    push();
    translate(width/2, height/2);
    drawHypotrochoid();
    pop();
}

//Epitrochoid curve (biggest curve)
function drawEpitrochoid() {
    //http://mathworld.wolfram.com/Epitrochoid.html
    
    var x1;
    var y1;
    
    //scale and rotation based on mouseY and mouseX
    var a1 = map(mouseY, 0, 480, 10, 70);
    var b1 = 20;
    var h1 = mouseX;
    
    strokeWeight(4);
    stroke('lightyellow');
    fill(mouseX, 150, mouseY); //fill based on the mouse
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t1 = map(i, 0, nPoints, 0, TWO_PI);
        //epitrochoid equation
        x1 = (a1 + b1) * cos(t1) - (h1 * cos((a1 + b1 / b1) * t1));
        y1 = (a1 + b1) * sin(t1) - (h1 * sin((a1 + b1 / b1) * t1));
        vertex(x1, y1);
    }
    endShape(CLOSE);
}

//Hypotrochoid curve
function drawHypotrochoid() {
    //http://mathworld.wolfram.com/Hypotrochoid.html
    
    //rainbow filled hypotrochoid
    var x2;
    var y2;
    
    //scale and rotation based on the mouse
    var a2 = map(mouseY, 0, 480, 80, 200);
    var b2 = 20;
    var h2 = mouseX / 10;
    
    strokeWeight(4);
    stroke('hotpink');
    fill(mouseX, mouseY, 200);
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t2 = map(i, 0, nPoints, 0, TWO_PI);
        //hypotrochoid equation
        x2 = (a2 - b2) * cos(t2) + h2 * cos((a2 - b2) / b2 * t2);
        y2 = (a2 - b2) * sin (t2) - h2 * sin((a2 - b2) / b2 * t2);
        vertex(x2, y2);
    }
    endShape(CLOSE);
   
    //green hypotrochoid with lines
    var x3;
    var y3;
    
    var a3 = 180;
    var b3 = map(mouseY, 480, 0, 180, 20);
    var h3 = -mouseX / 10;
    
    //array for the lines inside the curve
    var lineX = [];
    var lineY = [];
    
    strokeWeight(3);
    stroke('lightgreen');
    noFill();
    beginShape();
    for (var i = 0; i < nPoints; i++) {
        var t3 = map(i, 0, nPoints, 0, TWO_PI);
        //hypotrochoid equation
        x3 = (a3 - b3) * cos(t3) + h3 * cos((a3 - b3) / b3 * t3);
        y3 = (a3 - b3) * sin(t3) - h3 * sin((a3 - b3) / b3 * t3);
        vertex(x3, y3);
        lineX.push(x3);
        lineY.push(y3);
    }
    endShape(CLOSE);
    
    //draw the lines inside the curve with a for loop
    for (var i = 0; i < lineX.length - 1; i++) {
        strokeWeight(2);
        stroke(mouseX + mouseY, mouseY, 120);
        line(0, 0, lineX[i], lineY[i]);
    }   
}

I was intimidated at first looking at the instructions that said we had to create an image based on math curve functions, and I thought it would be very difficult to do, but it turned out to be pretty simple. I had a lot of fun researching the different roulette curves and seeing which ones did cool things with code. I played a lot with mouseX and mouseY, as well as scale, map(), and color. My favorite part of this project is that if you stop your mouse at a different point on the canvas, the epitrochoid curve changes into a completely different curve each time; it’s so interesting to see the crazy curves it can create by changing its a, b, and h values with the mouse’s coordinates.

First state: only one hypotrochoid curves
Second state: with both hypotrochoid curves

Sammie Kim – Looking Outwards – 07

Artificial Arcadia is a collaborative project between the KOSMOS architects and Fragmentin, an art practice based in Switzerland. With its spatial design inspired by the Swiss infrastructures like snow cannons, irrigation systems, and more, Artificial Arcadia inspires visitors to interact with the dynamic landscape in a performative scenographic landscape. This landscape is mapped with “bauprofile” markers, which are construction poles that show the intended location of future buildings, and they are topped with a white textile roof evoking the Swiss mountain range. The interactive element comes alive as visitors enter and move through the installation, where the poles position themselves at different heights and gradually fall to reference the melting levels of ice. The algorithms derives from the Swiss topography data, where a new portion of the Alps snow level map is randomly selected and analyzed every few minutes, then translated within the landscape. This project was inspiring as it provides a perspective towards our environment, particularly how it sparks debate regarding the artificial integration to a natural area. Likewise, Fragmentin’s work crosses the boundary between art and engineering, exploring the complex systems through form and interaction. 

“bauprofile” markers (Fragmentin)

Interactive installation space prompts visitors to move through (Fragmentin)
Artificial Arcadia – Measured and adjustable landscapes

Mari Kubota- Looking Outwards- 07

Radial Phototrail

Phototrails by Lev Manovich is a research project that uses media visualization techniques for exploring visual patterns, dynamics and structures in approximately 2.3 million user-generated photos from Instagram. This data visualization project scales the images to any size and organize them in any order, presenting, for example, all the images in a collection sorted by their dates, locations, or visual characteristics. There are many ways the images were laid out to visualize different aspects of the data. Techniques include radial, montage, photoplot, and points and lines layouts. 

This project drew my attention because of the way it presents data of photographs is through the photographs themselves. The unique characteristic of this data visualization is that it uses singular images to depict larger images that show patterns across a global scale. 

Looking Outwards Week 8

His talk:

One of his works I liked from his instagram:

His website: http://thesystemis.com/

Zach Lieberman describes himself as an “artist, researcher, hacker dedicated to exploring new modes of expression and play.” He studied Fine Arts at Hunter College and has a BFA and MFS in Design and Technology from Parsons, where he currently teaches. His works use technology in a way that augments the body’s ability to communicate, focusing on computer graphics, human-computer interaction, and computer vision.

Throughout the talk, Lieberman was very humorous, genuine, and relatable with his audience. He introduces himself by first talking about his relationship with his father and how his father inspires him. “The world needs stories. Storytelling isn’t about technique, it’s about being fully human.” His personal story is important in contextualizing his work.

I like the way he chose to introduce himself because I feel like it rang true for his work as a whole and the idea of human connection that he works toward.

He uses drawing (live demonstrations of drawing with code) as a vehicle to talk about his projects, as well as introducing other artists and works he likes. For example, using airplane wallpaper to introduce idea of connecting to other places and then connecting that to his project “Play the World”. I liked that project a lot, especially because of the surround sound speakers that serve as a reminder of your physical location in the world.